Un Cerchio è diviso in modo uniforme in sei pari triangoli
Ciao Marilynn,
in Primo luogo, vi racconto la mia ipotesi su ciò che la fotografia sia come:
- Ogni triangolo ha un vertice (angolo) al centro del cerchio
- Ogni triangolo ha gli angoli sulla circonferenza del cerchio (quindi, due lati di ogni triangolo è un raggio)
- I triangoli condividere i lati (non ci sono buchi allargati tra i triangoli)
Il quadro complessivo appare come un fiore, ogni triangolo è un petalo.

L’area sconosciuta è ciò che rimane intorno all’esterno del cerchio, tra la circonferenza e il lato esterno di ciascun triangolo. Questa area sconosciuta è divisa in sei sezioni congruenti (uguali in ogni modo – come i triangoli sono “uguali” in ogni modo – inclusa l’area, la lunghezza del lato e la lunghezza dell’arco). Non è chiaro se si intende l’area di un arco è Pi (non in realtà split Pie, anche se pronouced lo stesso), o tutte e sei le sezioni prese insieme è Pi. In quanto segue, assumerò che una delle sezioni esterne abbia un’area di Pi, in modo che l’area di tutte e sei le sezioni prese insieme sia 6 volte Pi. Dobbiamo trovare il raggio del cerchio, chiamarlo r.
Userò anche P per stare per Pi (o ca. 3.14). Ora, ci sono molte informazioni che possiamo guarnire dai triangoli:
- Gli angoli al centro sono tutti di 60 gradi. Questo perché i sei angoli al centro sono tutti uguali e un cerchio ha 360 gradi. Così fanno 360 edivided da 6.
- Ogni triangolo è isoscele. Questo perché due lati sono uguali (i lati che sono un raggio).
- Ogni triangolo, è infatti equilatero. Poiché è isoceles, anche i due angoli esterni sono uguali. Ma ci sono 180 gradi in un triangolo, 60 sono già usati nell’angolo centrale, lasciando 180-60=120 gradi per gli angoli esterni. Ma, 120 diviso 2 è 60 gradi, quindi tutti e tre gli angoli sono uguali, quindi è isoscle.
- Ogni lato in ogni triangolo è di lunghezza r. Questo perché abbiamo 6 triangoli equilateri congruenti (“uguali” in ogni modo) e perché due lati di ogni triangolo sono un raggio.
Dalla geometria dei triangoli, dobbiamo fare un po ‘ di algebra. Poiché conosciamo un’area e abbiamo bisogno di un raggio, abbiamo bisogno di una formula (o equazione) per il raggio in termini di area (in quanto segue, tieni presente l’obiettivo di una formula). L’area del cerchio è P*r2 (r2 significa r al quadrato e * significa moltiplicare) L’area delle sezioni rimanenti al di fuori di triangoli, ma all’interno del cerchio (un’area che già non essere di 6*P) può anche essere trovato sottraendo l’area dei triangoli dall’area del cerchio. Dobbiamo trovare un’area di uno dei triangoli equilateri.
Metodo 1 per calcolare un’area di un triangolo
L’area di un triangolo è b*h/2 È qui che è necessaria una trigonometria: tracciare una linea da un vertice a un lato opposto che divide il lato opposto a metà ed è ad angolo retto. Questo divide il triangolo in due congruenti ad angolo retto e triangoli, e il nuovo lato è l’altezza, la chiamiamo h. Abbiamo bisogno di trovare h.
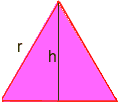
Utilizzando trig in uno dei triangoli ad angolo retto, abbiamo sin60 = h/r Ma sin60 = sqr(3)/2, dove sqr(3) significa che la radice quadrata di tre, così sqr(3)/2 = h/r moltiplicare entrambi i lati da r per ottenere h = r*sqr(3)/2 r Ora, l’area di un triangolo equilatero b*h/2 = (d)*(r*sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6*sqr(3)/4)) ordine di operazioni di calcolo su un calcolatore (con P=3.14): r= 5.896… Quindi, il raggio del cerchio è di ca. 5.9. Paolo