Utilizzo dei logaritmi nel mondo reale

I logaritmi sono ovunque. Hai mai usato le seguenti frasi?

• 6 cifre
• Doppia cifra
• Ordine di grandezza
• Tasso di interesse

Stai descrivendo i numeri in termini di poteri di 10, un logaritmo. E un tasso di interesse è il logaritmo della crescita di un investimento.

Sorpreso che i logaritmi siano così comuni? Anch’io. La maggior parte dei tentativi di matematica nel mondo reale (TM) sottolineano i logaritmi in qualche formula arcana, o fingono che siamo geologi affascinati dalla scala Richter. “Gli scienziati si preoccupano di registri, e si dovrebbe troppo. Inoltre, puoi immaginare un mondo senza zinco?”

No, no, no, no, no, no! (Mamma mia!)

La matematica esprime concetti con notazione come ” ln “o ” log”. Trovare “matematica nel mondo reale” significa incontrare idee nella vita e vedere come potrebbero essere scritte con la notazione. Non cercare i simboli letterali! Quand’e ‘ stata l’ultima volta che hai scritto un cartello di divisione? Quand’e ‘ stata l’ultima volta che hai fatto a pezzi del cibo?

Ok, ok, abbiamo capito: cosa sono i logaritmi?

I logaritmi trovano la causa di un effetto, cioè l’input per alcuni output

Un “effetto” comune sta vedendo crescere qualcosa, come passare da \$100 a \ \ 150 in 5 anni. Com’e ‘ successo? Non siamo sicuri, ma il logaritmo trova una possibile causa: un ritorno continuo di ln(150/100) / 5 = 8.1% rappresenterebbe questo cambiamento. Potrebbe non essere la causa reale (tutta la crescita è avvenuta nell’ultimo anno?), ma è una media liscia che possiamo confrontare con altri cambiamenti.

A proposito, la nozione di “causa ed effetto” è sfumata. Perché 1000 è più grande di 100?

• 100 è 10, che è cresciuto da solo per 2 periodi di tempo ($10 * 10$)
• 1000 è 10, che è cresciuto da solo per 3 periodi di tempo ($10 * 10 * 10$)

Possiamo pensare di numeri come uscite (1000 “1000 uscite”) e input (“quante volte 10 bisogno di crescere, di fare quelle uscite?”). Quindi,

1000 outputs > 100 outputs

perché

3 inputs > 2 inputs

O in altre parole:

log(1000) > log(100)

Perché questo è utile?

I logaritmi mettono i numeri su una scala adatta all’uomo.

Grandi numeri rompono il nostro cervello. Milioni e trilioni sono “davvero grandi” anche se un milione di secondi è di 12 giorni e un trilione di secondi è di 30.000 anni. E ‘ la differenza tra un anno di vacanza americana e la totalità della civiltà umana.

Il trucco per superare la “cecità numerica enorme” è scrivere numeri in termini di “input” (cioè la loro base di potenza 10). Questa scala più piccola (da 0 a 100) è molto più facile da afferrare:

• potenza di 0 = $10^0$ = 1 (singolo elemento)
• potenza di 1 = $10^1$ = 10
• potenza 3 = $10^3$ = migliaia di euro
• potenza di 6 = $10^6$ = milioni di
• potenza di 9 = $10^9$ = miliardi
• potenza di 12 = $10^12$ = trilioni
• potenza di 23 = $10^23$ = numero di molecole in una dozzina di grammi di carbonio
• una potenza di 80 = $10^80$ = numero di molecole dell’universo

Una scala da 0 a 80 ci ha portato da un unico elemento per il numero di cose nell’universo. Non troppo malandato.

I logaritmi contano la moltiplicazione come passi

I logaritmi descrivono i cambiamenti in termini di moltiplicazione: negli esempi sopra, ogni passo è 10 volte più grande. Con il registro naturale, ogni passo è ” e “(2.71828…) volte di più.

Quando si ha a che fare con una serie di moltiplicazioni, i logaritmi aiutano a “contarli”, proprio come l’aggiunta conta per noi quando vengono aggiunti effetti.

Mostrami la matematica

Tempo per la carne: vediamo dove appaiono i logaritmi!

Stipendio a sei cifre o spesa a 2 cifre

Stiamo descrivendo i numeri in termini di cifre, cioè quanti poteri di 10 hanno (sono nelle decine, centinaia, migliaia, diecimila, ecc.). Aggiungere una cifra significa “moltiplicare per 10”, cioè

I logaritmi contano il numero di moltiplicazioni aggiunte, quindi a partire da 1 (una singola cifra) aggiungiamo altre 5 cifre ($10^5$) e 100.000 ottengono un risultato a 6 cifre. Parlare di” 6 “invece di” Centomila ” è l’essenza dei logaritmi. Dà un ruvido senso di scala senza saltare nei dettagli.

Domanda bonus: Come descriveresti 500.000? Dire “6 figura” è fuorviante perché 6-figure spesso implica qualcosa di più vicino a 100.000. Sarebbe” 6.5 figura ” lavoro?

Non proprio. Nella nostra testa, 6.5 significa “a metà strada” tra 6 e 7 figure, ma questa è la mentalità di una vipera. Con logaritmi a”.5 ” significa a metà strada in termini di moltiplicazione, cioè la radice quadrata (9 9^.5 means significa che la radice quadrata di 9 3 3 è a metà strada in termini di moltiplicazione perché è da 1 a 3 e da 3 a 9).

Prendendo log (500.000) otteniamo 5.7, aggiungiamo 1 per la cifra extra e possiamo dire “500.000 è un 6.7 numero di figura”. Provalo qui:

Ordine di grandezza

Noi geek amiamo questa frase. Significa approssimativamente “differenza 10x” ma suona più fresco di “1 cifra più grande”.

Nei computer, dove tutto è contato con bit (1 o 0), ogni bit ha un effetto di raddoppio (non 10x). Quindi passare da 8 a 16 bit è “8 ordini di grandezza” o 2 2^8 = 256 times volte più grande. (“Più grande” in questo caso si riferisce alla quantità di memoria che può essere indirizzata.) Passando da 16 a 32 bit significa un extra di 16 ordini di grandezza, o 2 2^16 ~ ~ 65.536 volte più memoria che può essere indirizzata.

Tassi di interesse

Come possiamo calcolare i tassi di crescita? Un paese non intende crescere all ‘ 8,56% all’anno. Si guarda al PIL un anno e al PIL il prossimo, e si prende il logaritmo per trovare il tasso di crescita implicito.

Le mie due interpretazioni preferite del logaritmo naturale (ln (x)), cioè il log 1.5:

• Supponendo una crescita del 100%, quanto tempo hai bisogno di crescere per arrivare a 1.5? (.405, meno della metà del periodo di tempo)
• Supponendo 1 unità di tempo, quanto velocemente hai bisogno di crescere per arrivare a 1.5? (40.5% all’anno, continuamente composto)

I logaritmi sono come capire quanto velocemente stiamo crescendo.

Scala di misurazione: Google PageRank

Google dà ogni pagina sul web un punteggio (PageRank) che è una misura approssimativa di autorità / importanza. Questa è una scala logaritmica, che nella mia testa significa “PageRank conta il numero di cifre nel tuo punteggio”.

Quindi, un sito con pagerank 2 (“2 cifre”) è 10 volte più popolare di un sito PageRank 1. Il mio sito è PageRank 5 e CNN ha PageRank 9, quindi c’è una differenza di 4 ordini di grandezza ($10^4$ = 10,000).

In parole povere, ottengo circa 7000 visite / giorno. Usando la mia matematica della busta, posso indovinare che la CNN ottiene circa 7000 * 10.000 = 70 milioni di visite / giorno. (Come ho fatto? Nella mia testa, penso 7 7k * 10k = 70 * k * k = 70 * M$). Potrebbero avere un paio di volte di più (100M, 200M) ma probabilmente non fino a 700M.

Google trasmette molte informazioni con una scala molto approssimativa (1-10).

Scala di misura: Richter, Decibel, ecc.

Sospiro. Siamo al tipico esempio di “logaritmi nel mondo reale”: scala Richter e Decibel. L’idea è di mettere eventi che possono variare drasticamente (terremoti) su una singola scala con un piccolo intervallo (in genere da 1 a 10). Proprio come PageRank, ogni aumento di 1 punto è un miglioramento 10x in potenza. Il più grande terremoto registrato dall’uomo è stato 9.5; l’impatto della penisola dello Yucatán, che probabilmente ha reso i dinosauri estinti, è stato 13.

I decibel sono simili, anche se possono essere negativi. I suoni possono passare da intensamente tranquillo (pindrop) a estremamente forte (aereo) e il nostro cervello in grado di elaborare tutto. In realtà, il suono del motore di un aereo è milioni (miliardi, trilioni) di volte più potente di un pindrop, ed è scomodo avere una scala che va da 1 a un gazillion. I registri mantengono tutto su una scala ragionevole.

Grafici logaritmici

Vedrai spesso gli elementi tracciati su una “scala di log”. Nella mia testa, questo significa che un lato sta contando “numero di cifre” o “numero di moltiplicazioni”, non il valore stesso. Ancora una volta, questo aiuta a mostrare eventi selvaggiamente variabili su una singola scala (passando da 1 a 10, non da 1 a miliardi).

La legge di Moore è un grande esempio: raddoppiamo il numero di transistor ogni 18 mesi (immagine gentilmente concessa da Wikipedia).

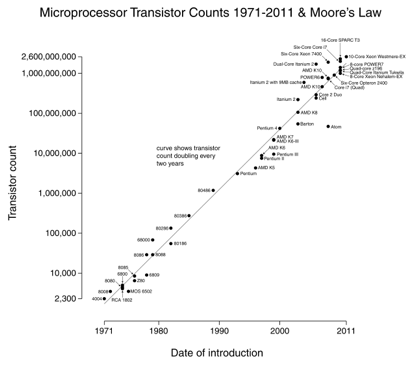
La cosa bella dei grafici a scala di log è che i cambiamenti esponenziali (velocità del processore) appaiono come una linea retta. Crescere 10x all’anno significa che stai marciando costantemente sulla scala delle “cifre”.

In avanti e verso l’alto

Se un concetto è ben noto ma non ben amato, significa che abbiamo bisogno di costruire la nostra intuizione. Trova le analogie che funzionano e non accontentarti della sbobba che un libro di testo tirerà fuori. Nella mia testa:

• I logaritmi trovano la causa principale di un effetto (vedi crescita, trova tasso di interesse)
• Aiutano a contare moltiplicazioni o cifre, con il bonus dei conteggi parziali (500k è un numero di 6,7 cifre)

Buona matematica.

Altri Post In Questa Serie

1. Una Guida Intuitiva Per Funzioni Esponenziali & e
2. Demistificare il Logaritmo Naturale (ln)
3. Una Guida Visiva per Semplice, Composto e Continuo Tassi di Interesse
4. Definizioni Comuni e (Colorato)
5. Comprensione Esponenti (Perché 0^0 = 1?)
6. Usare i logaritmi nel mondo reale
7. Come pensare con esponenti e logaritmi
8. Capire la crescita discreta rispetto a quella continua
9. Cosa significa veramente un esponente?
10. Q: Perché è e speciale? (2.718…, non 2, 3.7 o un altro numero?)