ンサーによるダブルチェックを均一に分かれている等しい三角形
こんにちはMarilynn,
まず、伝えていければと思いま私の想定どお写真のように見え:
- 各三角形は、頂点(コーナー)センターでは、円
- 各三角形は、コーナーの周囲をおおっていて、そのサークルなので、双方の三角形は半径)
- の三角シェア(ありませんgapes間の三角形)
の全体像が見え用のパーソナルコンピュータ-各三角形は、花びら.

未知の領域は、円周と各三角形の外側の間の円の外側の周りに残っているものです。 この未知の領域は、6つの合同なセクションに分割されます(すべての方法で等しい-三角形がすべての方法で”等しい”ように-面積、辺の長さ、円弧の長さ 1つの円弧の面積がPiであることを意味するのか(実際には分割されたパイではありませんが、同じ発音です)、または6つのセクションすべてがPiで 以下では、外側のセクションの1つが円周率の面積を持つと仮定し、6つのセクションすべての面積を合わせて6倍の円周率にすると仮定します。 円の半径を見つけてrと呼ぶ必要があります。
私はまた、Pi(または約)を表すためにPを使用します。 3.14). さて、三角形から飾ることができる多くの情報があります:
- 中心の角度はすべて60度です。 これは、中心の6つの角度がすべて等しく、円が360度であるためです。 360を6で割ったものです。
- 各三角形は二等辺三角形です。 これは、2つの辺が等しい(半径である辺)ためです。
- 各三角形は、実際には正三角形です。 それはiscocelesなので、二つの外側の角度も等しいです。 しかし、三角形には180度があり、60はすでに中心角で使用されており、外側の角度には180-60=120度を残しています。 しかし、120を2で割ったものは60度なので、3つの角度はすべて等しいので、isosclesです。
- すべての三角形のすべての辺の長さはrです。 これは、6つの合同(あらゆる点で「等しい」)正三角形があり、すべての三角形の2つの辺が半径であるためです。
三角形の幾何学から、いくつかの代数を行う必要があります。 私たちは面積を知っていて、半径が必要なので、面積の観点から半径の式(または式)が必要です(以下では、式の目標を念頭に置いてください)。 円の面積はP*r2(r2はrの二乗を意味し、*は乗算を意味します)三角形の外側の残りの部分の面積ですが、円の内側(すでに6*Pになる領域)は、円の面積から三角形の面積を減算することによっても見つけることができます。 正三角形の1つの領域を見つける必要があります。
三角形の面積を計算するための方法1
三角形の面積はb*h/2ですこれは、いくつかの三角法が必要な場所です:反対側を半分に分割し、直角である これは、正三角形を2つの合同な直角三角形に分割し、新しい辺は高さであり、それをhと呼びます。hを見つける必要があります.
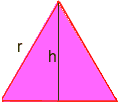
直角三角形の1つでtrigを使用すると、sin60=h/rが得られますが、sin60=sqr(3)/2、ここで、sqr(3)は3つの平方根を意味するので、sqr(3)/2=h/r両側にrを掛けてh=r*sqr(3)/2rを得ます今、1つの正三角形の面積はb*h/2=(r)*(r*sqr)である。(3)/2)/2 = (r2)*sqr(3)/4r=sqr(6*P/(P-6*sqr(3)/4))計算機で計算する操作の順序を使用します(P=3.14):r=5.896。.. したがって、円の半径は約です。 5.9. ポール