太陽系:地球と月
惑星は私たちから数十億キロ離れています。 このような大きな数の使用を避けるために、距離の単位、すなわち地球と太陽の間の平均距離、149,600,000kmとして天文単位(AU)が採用されています。光はこの距離をカバーするために8分19秒かかります。
太陽系の大きさは冥王星の40AUの軌道を超えており、太陽の引力が私たちに最も近い星の引力に等しいものと定義されています。 太陽系の大きさは、1.5 105AUのオーダーになります。 明らかに、これらの次元は、銀河や目に見える宇宙の次元に比べて非常に小さいです。 これらの巨大な距離を測定するために取られる単位は、光年と206 265AUまたは3.26光年に相当するパーセクです。
太陽系の惑星は、水星、金星、地球、火星によって形成された地球型惑星群と、木星、土星、天王星、海王星によって形成された巨大惑星群の2つのグループ
金星と水星を除く全ての惑星には衛星があり、その大部分は巨大惑星に属している。 地球、木星、土星、海王星は最大の衛星を持っています:月、ガリレオ(イオ、エウロパ、ガニメデ、カリスト)、土星の衛星タイタンと海王星のトリトンによって発見された木星の衛星。
小惑星は、太陽から2.75AUの平均距離で、火星と木星の軌道の間の広大な環状領域を占めています。 最大の小惑星は、1000キロの直径を有するセレスです。
約600個の彗星がカタログ化されており、短周期(20年未満)と長周期(20年以上)の二つのグループに分かれています。 彗星の起源については、オランダの天文学者J.オールトのものを含むいくつかの仮説がある。
惑星間空間で言及されている天体に加えて、大きさの異なる多数の粒子があり、主に1グラムの1000分の1または1000分の1の質量を持つ粒子で、流星塵と呼ばれています。 これらの粒子の形成は、おそらくより大きな天体(小惑星)の衝突と、太陽系の存在と進化を通じてそれらの連続的な断片化によるものです。
流星塵は、これらの塵粒子による光の分散により、夕暮れ後または夜明け前に観測される黄道光の現象の原因となっています。 ほとんどの粒子は、地球の大気に入ると蒸発し(高度80〜120km)、わずかな割合で地球の表面に到達します。
それでは、太陽系の惑星に関連するいくつかのデータを見てみましょう
最初の太陽
| 天体 | ラジオ | 質量 |
|---|---|---|
| 太陽 | 6.96×108m | 1.98×1030kg |
その後、土地の外に
| 天体 | 半長軸 | 周期 | 質量 |
|---|---|---|---|
| 地球 | 149.6·109m | 1年=365.26日 | 5.98*1024キロ |
残りの惑星は
| 惑星 | 半長軸(AU) | 離心率 | 周期(年) | 質量 |
|---|---|---|---|---|
| マーキュリー | 0.387 | 0.206 | 0.24 | 0.06 |
| ヴィーナス | 0.723 | 0.007 | 0.62 | 0.82 |
| 地球 | 1.000 | 0.017 | 1.00 | 1.00 |
| マーズ | 1.524 | 0.093 | 1.88 | 0.11 |
| ジュピター | 5.203 | 0.048 | 11.86 | 318 |
| サターン | 9.539 | 0.056 | 29.46 | 95.1 |
| 天王星 | 19.182 | 0.047 | 84.01 | 14.6 |
| ネプチューン | 30.058 | 0.009 | 164.8 | 17.2 |
次の表では、補足データとして提供されています:
- 黄道に対する惑星の軌道面(地球の軌道面)の傾き)
- その軸を中心とした回転の周期。 水星や金星のような惑星のためにこの大きさを測定することは非常に困難でした。 木星、土星、天王星、海王星のガス状殻は、緯度によって回転周期が異なるという差動回転の性質を持っています。
- 軌道の平面に対する回転軸の傾き。 金星の場合、それは軸の傾きが3πであるが回転方向が逆であると言うことに相当する177πである。 天王星にも同じ議論が適用され、天王星の回転軸が軌道のほぼ平面にあることを示しています。
| 惑星 | 軌道の傾き | 自転周期 | 密度g/cm3 | 電波赤道(km) | 軸の傾き | いいえ。 衛星の |
|---|---|---|---|---|---|---|
| マーキュリー | 7位0 | 58.6 | 5.44 | 2 439 | <30㎡ | 0 |
| 金星 | 3位。4 | 243 | 5.24 | 6 051 | 177 ° | 0 |
| 地球 | 0 | 23時間.9 | 5.52 | 6 378 | 第23回5 | 1 |
| 火星 | 1st.8 | 24h.6 | 3.95 | 3 394 | 25㎡2 | 2 |
| 木星 | 1.3 | 9h.9 | 1.33 | 71 398 | 第3回1 | 16 |
| サターン | 2位。5 | 10h.2 | 0.69 | 60 000 | 26㎡4 | 17 |
| 天王星 | 0º。8 | 10h.8 | 1.26 | 25 400 | 98㎡ | 5 |
| 海王星 | 1st.8 | 15h.8 | 1.67 | 24 750 | 29㎡ | 2 |
衛星
最後に、惑星の主要な衛星に関するいくつかのデータを提供します。 木星と土星には火星よりもはるかに大きい多くの衛星がありますが、サイズが似ているか月よりも大きい衛星だけに言及しています。
| 惑星 | 衛星 | 密度g/cm3 | 平均半径(km) | 電波軌道(103km) | 周期(日) | 衛星 | 密度g/cm3 | 平均半径(km) | 電波軌道(103km) | 周期(日)) |
|---|---|---|---|---|---|---|---|---|---|---|
| 地球 | 月 | 3.33 | 1 738 | 384.4 | 27.32 | |||||
| 火星 | フォボス | 2.1 | 13.5 | 9.38 | 0.319 | |||||
| ダイモス | 2.1 | 7.5 | 23.46 | 1.262 | ||||||
| 木星 | イオ | 3.53 | 1 820 | 421.6 | 1.769 | |||||
| ヨーロッパ | 3.03 | 1 565 | 670.9 | 3.551 | ||||||
| ガニメデ | 1.93 | 2 638 | 1 070 | 7.155 | ||||||
| カリスト | 1.83 | 2 410 | 1 880 | 16.689 | ||||||
| 土星 | タイタン | 1.9 | 2 575 | 1 221.9 | 15.95 | |||||
| ネプチューン | イモリ | 2 200 | 394.7 | 5.84 |
活動
- は、衛星の電波データと公転周期から木星の質量を決定します。
- その惑星の質量と衛星の回転周期から惑星木星の衛星の軌道半径を決定します。
- 質量Mと半径Rまたは密度θと半径のデータから、惑星およびいくつかの衛星の表面上の重力場gの強度を決定します。<9474><8438>g=G M R2=4÷3GpR<8650><8438>データ:定数Gは6です。67*10-11Nm2/kg2
例:イオの軌道の半径が421,600kmで、その公転周期が1,769日であることを知っている惑星木星の質量を決定する。 事実:定数Gは6.67*10-11Nm2/kg2
: 衛星カリストの軌道半径を計算するその回転周期が16.689日であり、惑星木星の質量が1.901·1027kgであることを知っている。 データ:定数Gは6.67*10-11Nm2/kg2
月
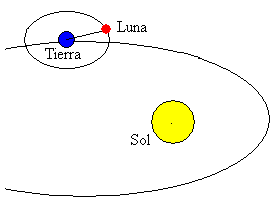
月は太陽系で最大の体の一つです。 その軌道はほぼ円形(離心率θ=0.05)であり、その軌道面は地球の軌道面に対して5π傾斜している。
地球の中心と月の間の平均距離は384,400kmです。地球の周りの自転周期は27,322日である。 太陽に対する月の位置の変化は、月の位相を生じさせる。
地球が月に及ぼす潮汐力の影響により、月は常に地球の観測者と同じ顔をしています。 これは、その軸の周りの月の回転周期が、地球の周りの軌道を完了するのにかかる時間と一致することを意味します。
月は人類を最も魅了してきた天体です。 旧ソ連は1959年に月の表面に着陸した自動船を最初に送りました。 1969年7月20日、ニール・アームストロングはエドウィン・オルドリンと共にアポロ11号のミッションの一環として月面を歩いた最初の人物であった。 アメリカの宇宙飛行士の月への最後の訪問は1972年に行われました。
月の起源は不確かなようで、いくつかの説があります:
-
これは、星雲からの材料と同時に地球を形成しました
-
天体は二つの部分に分かれており、地球と月を生み出しています
-
月は他の場所で形成され、地球によって捕獲されたこと
-
地球が大きなサイズ(火星以上の大きさ)の天体と衝突し、月がこの衝突から追放された材料で形成されたこと。
後者の理論は、現時点では、科学界によって最も受け入れられているようです。
ムーンパス
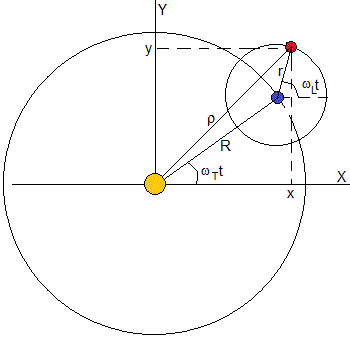
惑星とその衛星を考えてみましょう。 惑星は、一定の角速度wT=2π/PTを持つ恒星の周りの半径Rの円軌道を記述し、PTは完全な回転につながる期間または時間である。 衛星のつの円形軌道coplanariaの半径rは一定の角速度wL=2π/PLは、PLの期間や時間を完全に革命
の位置は衛星に対して参照システムの原点が、星は
x=Rcos(ω T)+rcos(ω L t)y=Risiko(ω T)+risiko(ω L t)
はα=wT/wL
{x=Rcos(α ω L t)+rcos(ω L t)y=Risiko(α ω L t)+risiko(ω L t){x=Rcos(α2π P L t)+rcos(2π P L t)y=Risiko(α2π P L t)+risiko(2π P L t)
ち着τ=t/PL
x R=cos(α·2θ)+r r Cos(2θ)およびR=Sin(α·2θ)+r r sin(2θ)
α=0.1およびr/rの三つの値に対する衛星の軌道を表します。
- r/r<α。 例えば、r/R=0.05
- r/R=αである。 例えば、r/r=0.1
- r/R>αである。 例:r/R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
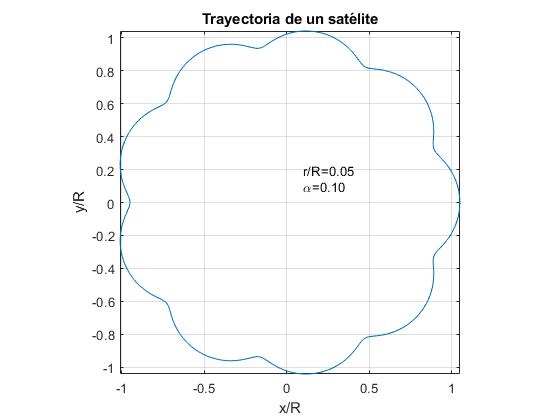
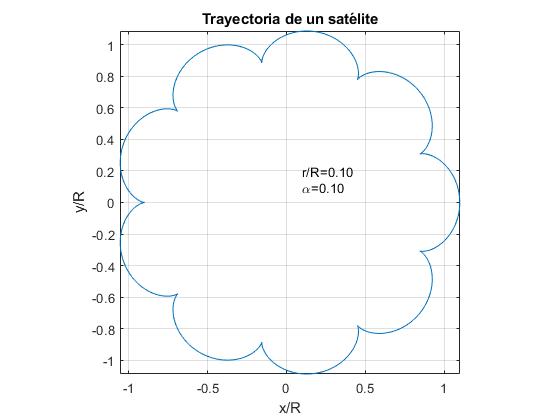
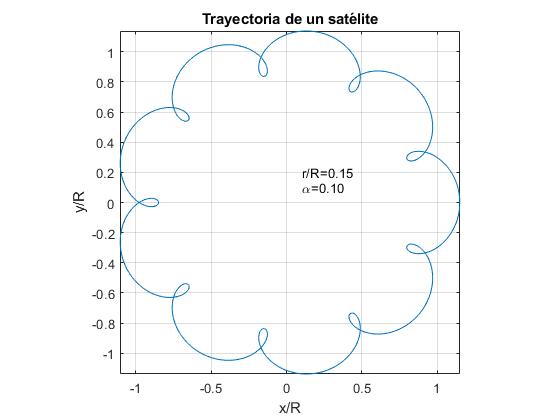
地球と月の場合、データは次のとおりです:
- 月の軌道半径:r=384.4·106m、周期PL=27.32d
- 地球軌道半径: R=149.6·109m、周期PT=365.26d
α=wT/wL=PL/PT=0.0748。 r/R=0.0026
月の軌道は最初の図に似ています。 これらのαとr/Rの値に対する月の軌道のグラフ表現では、太陽と月の間の半径方向の距離の振動を理解していません
月の加速度
太陽から月までの距離θは、
θ2=x2+y2=R2+r2+2rrcos((ω L−ω T)t)
加速度の矩形成分を計算します
{dx dt=−ω t risiko(ω T)−Ω L Risiko(Ω L T)Dy Dt=Ω t rcos(Ω T)+Ω L Rcos(Ω L T){a x=d2x d t2=−ω t2rcos(ω t)−ω l2rcos(ω L T)y= d2y d2=−ω T2Risiko(ω T)−ω L2risiko(ω L t)
ラジアル部品の加速
最小値と最大値が得られる場合cos((wL-wT)t)=±1
max=−ω R T2 2+ω L2r2+(ω T2+ω L2)Rr R2+r2+2rr=−ω R T2+ω L2r) min=−ω R T2 2+ω L2r2−(ω T2+ω L2)Rr R2+r2-2rr=−ω T2R−ω L2r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
月は太陽系で唯一の衛星であり、加速度の半径成分が負であり、”月は太陽に向かって落ちる”と言われています。
月の位相
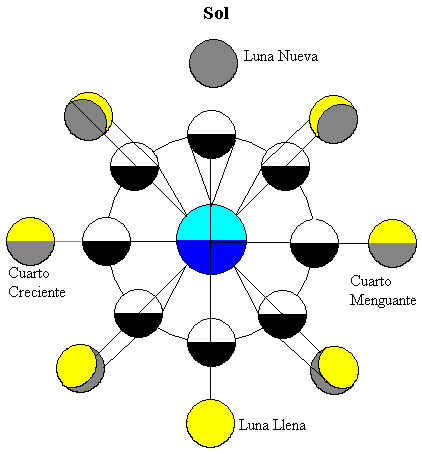
図は、地球の周りの軌道上で異なる位置にある月を示しています。 太陽は遠く離れて両方の天体を照らしています(図の上部)
月の半分は太陽(白色)によって照らされ、地球に最も近い月の半分は地上の観測者によって 月が地球の周りを移動すると、私たちは太陽(黄色の領域)によって照らされた部分の異なる部分を見ます。
-
月が地球と太陽の間にあるとき、地球に最も近い月の部分は暗いので、私たちは月を見ることができません、この段階は新月と呼ばれています。
-
地球が太陽と月の間にあるとき、地球に最も近い月の部分は照らされた半分であり、この段階は満月と呼ばれます。
-
月が中間位置にあるとき、地球の最も近い部分の半分だけが照らされます。 したがって、私たちは月の四分の一しか見ておらず、これらの二つの位相は四分の一と呼ばれ、地球から見える照らされた部分が成長するか減少する傾向があるかどうかに応じて増加または減少します。
メモ: このインタラクティブなプログラムは、月の位相を説明しようとしますが、それは黄道の平面(太陽の周りの地球の軌道)、または黄道の平面に法線と約23ºである地球の軸の向きと5°の角度を形成する月の軌道の忠実な表現です。
読者が月の軸周りの回転周期と地球の周りの軌道を完了するのにかかる時間の一致を理解できるように、月を横切って赤い線が描かれているため、月は常に地球と同じ顔をしている。
月の食
月食は、月が満ち欠けになっているときや、太陽、地球、月が直線になっているときに発生します。 そして、図に示すように、月は地球によって生成された影にあります。
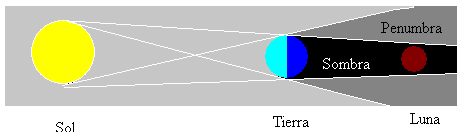
月食には他の種類があり、これらは3つの天体の位置合わせに依存します。 月は点灯していない領域(影)または部分的に点灯している(半影)かもしれません。
日食は月が太陽と地球の間に立っているときに起こり、月は新しい段階にあります。 月は太陽の400倍小さいですが、月は地球に400倍近いので、地球から見た両方の体の見かけの大きさはほぼ同じです。 地球上の月によって投影された影のゾーンで観察された場合、月は、このように、太陽の皆既日食を生成することができます。
ムーンデータ
| 質量(kg) | 7.349·1022 |
| 半径(km) | 1737. 4 |
| 平均密度(g/cm3) | 3.34 |
| 地球までの平均距離(km) | 384 000 |
| 軌道の期間(日) | 27.32166 |
| 赤道での重力加速度(m/s2) | 1.62 |
| 軌道の離心率 | 0.0549 |
| 軌道の傾き(度) | 5.1454 |
-
周期が27.32日であることを知っている地球の周りの月の円軌道の半径を計算します。 また、月の速度を計算します。 データ:G=6.67*10-11Nm2/kg2、地球の質量はM=5.98*1024kgです。
-
月の表面上の重力gの加速度を計算します。
-
太陽の直径と月の直径の間の商を計算します。 太陽と地球と月と地球の間の平均距離の比を計算します。 データ:太陽半径6.96·108m、中つ国-太陽距離1.49·1011m
-
地球の中心から測定された地球-月系の質量中心の位置を計算します。
-
月の地球の引力を計算し、それを月の太陽の引力と比較します。 測地基準系:太陽質量、1.98*1030kg
参考文献
M.Marov。 太陽系の惑星。 出版社ミール。
惑星の詳細はこちら太陽系には何個の惑星がありますか?. ComofuncionaQue.com
セクション”月の軌道”
David C.Johnston。 並進運動と回転運動の重ね合わせとしての物理学におけるサイクロイド経路。 アム… J.Phys.87(10),October2019,pp.808-810
月は常に太陽に向かって向きを変える。 数学のページ。