現実の世界で対数を使う

BY admin
|

対数はどこにでもあります。 今まで次のフレーズを使用しますか？

  • 6 数字
  • 二桁
  • 大きさの順
  • 金利

あなたは10の累乗、対数で数を記述しています。 そして、金利は投資の成長の対数です。

私も 現実世界（TM）の数学のほとんどの試みは、いくつかの難解な公式の対数を指摘するか、私たちがリヒタースケールに魅了された地質学者であるふりをします。 “科学者はログを気にし、あなたもすべきです。 また、亜鉛のない世界を想像できますか？”

いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、いや、 （ママミーア！)

数学は”ln”や”log”のような表記で概念を表現します。 「現実世界の数学」を見つけることは、人生の中でアイデアに遭遇し、それらがどのように表記法で書くことができるかを見ることを意味します。 リテラル記号を探すな！ あなたが最後に部門記号を書いたのはいつですか？ 最後に食べ物を切り刻んだのはいつですか？

Ok、ok、私たちはそれを得る：対数は何ですか？

対数は、効果の原因、すなわちいくつかの出力の入力を見つける

一般的な”効果”は、5年間で\100から\150になるような何かが成長するのを見ています。 これはどのように起こったのですか？ 私たちは確信していませんが、対数は考えられる原因を見つけます：ln（150/100）/5=8.1％の連続的なリターンがその変化を説明します。 それは実際の原因ではないかもしれません（すべての成長は最終年に起こりましたか？）、しかし、それは我々が他の変更と比較することができます滑らかな平均です。

ところで、”原因と結果”という概念は微妙です。 なぜ1000が100より大きいのですか？

  • 100 は10年に2回、単独で成長していますが、($10 * 10$)
  • 1000 10月には3年間単独で成長した。($10 * 10 * 10$)

数値を出力（1000は「1000出力」）と入力（「これらの出力を行うために10を何回成長させる必要がありますか？”). だから,

1000 outputs > 100 outputs

3 inputs > 2 inputs

または他の言葉であるため:

log(1000) > log(100)

これはなぜ便利ですか？

対数は数字を人間に優しいスケールにします。

多数は私達の頭脳を壊す。 百万秒は12日であり、兆秒は30,000年であるにもかかわらず、何百万と兆は”本当に大きい”です。 それはアメリカの休暇の年と人間の文明の全体の違いです。

“膨大な数の失明”を克服するためのトリックは、”入力”（すなわち、それらのべき乗10）の観点から数を書くことです。 この小さなスケール（0から100）は、把握する方がはるかに簡単です:

  • 電力の0 = $10^0$ = 1 (単品)
  • 電力の1 = $10^1$ = 10
  • 電力の3=$10^3$=千
  • 電力の6=$10^6$=百万
  • 電力の9=$10^9$=億
  • 電12=$10^12$=兆
  • 電23=$10^23$=数の分子が数十グラムの炭素
  • 電力の80=$10^80$=数の分子宇宙

対数は乗算をステップとしてカウントします

対数は乗算の点で変化を記述します：上記の例では、各ステップは10倍大きくなります。 自然対数では、各ステップは”e”(2.71828…）倍以上。

一連の乗算を扱うとき、対数は効果が追加されたときの加算カウントと同じように、それらを”カウント”するのに役立ちます。

私に数学を表示

肉のための時間：対数が現れる場所を見てみましょう！

6桁の給与または2桁の経費

数字を数字で記述しています。 彼らが持っている10の力の数（彼らは数十、数百、数千、数万などにありますか？). 数字を追加することは、”10を掛ける”ことを意味します。

\テキスト{1\テキスト{}\cdot10\cdot10\cdot10\cdot10\cdot10\テキスト{}\cdot10\cdot10\cdot10\テキスト{}{} = 10^5 = 100,000}

対数は加算された乗算の数を数えるので、1（1桁）から始めてさらに5桁（1 10^5$）を追加し、100,000は6桁の結果を得ます。 「10万」の代わりに「6」について話すことは、対数の本質です。 それは細部に跳ばないでスケールの荒い感覚を与える。

ボーナス質問：あなたは500,000をどのように説明しますか？ 6-数字は、多くの場合、100,000に近い何かを意味するので、”6図”と言って誤解を招くことです。 “6.5図”は動作しますか？

そうではありません。 私たちの頭の中では、6.5は6と7の数字の間の”途中”を意味しますが、それは加算器の考え方です。 対数を使って”。5″は、乗算の途中、すなわち平方根（$9^。5πは、9-3の平方根が1から3と3から9であるため、乗算の途中であることを意味します）。

Log(500,000)を取ると、5.7が得られ、余分な数字に1を加算すると、”500,000は6です。背番号は”7″。 ここで試してみてください：

大きさの順

私たちオタクはこのフレーズが大好きです。 それはおおよそ”10倍の違い”を意味しますが、”1桁大きい”よりも涼しい音だけです。

すべてがビット（1または0）でカウントされるコンピュータでは、各ビットは倍加効果を持ちます（10倍ではありません）。 したがって、8から16ビットになると、”8桁”または$2^8=256times倍になります。 （この場合の「大きい」とは、アドレス指定できるメモリの量を指します。）16から32ビットになることは、余分な16桁、つまりaddressed2^16~〜65,536倍のメモリを意味します。

金利

成長率をどのように把握するのですか？ 国は年間8.56％で成長するつもりはありません。 あなたは1年のGDPと次のGDPを見て、対数を取って暗黙の成長率を見つけます。

自然対数（ln（x））の私の2つのお気に入りの解釈、すなわちの自然対数1.5:

  • 100％の成長を仮定すると、1.5に到達するためにどのくらい成長する必要がありますか？ (.405、時間の半分以下）
  • 1単位の時間を仮定すると、1.5に達するためにどれくらい速く成長する必要がありますか？ (40.年間5％、継続的に配合)

対数は、私たちが成長しているどのくらいの速さを把握する方法です。

測定スケール：Google PageRank

Googleは、ウェブ上のすべてのページに権限/重要性の大まかな尺度であるスコア（PageRank）を与えます。 これは私の頭の中で”PageRankはあなたのスコアの桁数を数える”ことを意味する対数スケールです。

だから、pagerank2（”2桁”）を持つサイトは、PageRank1サイトよりも10倍人気があります。 私のサイトはPageRank5であり、CNNにはPageRank9があるので、4桁の違いがあります($10^4$ = 10,000).

大まかに言えば、私は約7000訪問/日を取得します。 私の封筒の数学を使って、私はCNNが約7000*10,000=7000万回の訪問/日を得ると推測することができます。 （どうやってやったんですか？ 私の頭の中で、私はthink7k*10k=70*k*k=70*M Mと思います）。 彼らはそれよりも数倍（100M、200M）を持っているかもしれませんが、おそらく700Mまではありません。

Googleは非常に大まかなスケール（1-10）で多くの情報を伝えます。

測定スケール：リヒター、デシベルなど

ため息。 私たちは典型的な”現実世界の対数”の例にいます：リヒタースケールとデシベル。 アイデアは、小さな範囲（通常は1から10）で単一のスケールで大幅に変化する可能性のあるイベント（地震）を置くことです。 ちょうどPageRankのように、各1ポイントの増加は力の10倍の改善である。 人間が記録した最大の地震は9.5であり、恐竜を絶滅させた可能性が高いユカタン半島の影響は13であった。

デシベルは似ていますが、負になる可能性があります。 音は激しく静か（ピンドロップ）から非常に騒々しい（飛行機）に行くことができ、私たちの脳はそれをすべて処理することができます。 実際には、飛行機のエンジンの音は、ピンドロップよりも数百万（数十億、数兆）倍強力であり、1から数十億になるスケールを持つことは不便です。 ログはすべてを合理的な規模に保ちます。

対数グラフ

多くの場合、”対数スケール”でプロットされた項目が表示されます。 私の頭の中では、これは片側が値自体ではなく「桁数」または「乗算数」を数えていることを意味します。 繰り返しますが、これは1つのスケールで乱暴に変化するイベントを表示するのに役立ちます（1から10まで、1から数十億までではありません）。

ムーアの法則は良い例です: 私たちは18ヶ月ごとにトランジスタの数を倍増させます（画像提供Wikipedia）。

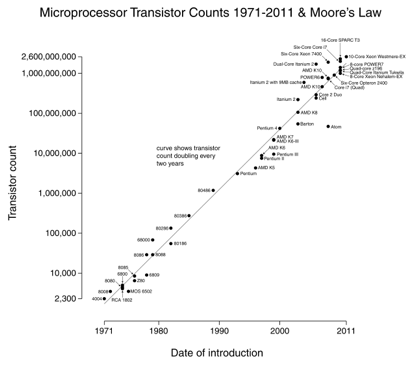
ムーアの法則

対数スケールグラフについてのきちんとしたことは、指数関数的変化（プロセッサ速度）が直線として現れることです。 年間10倍の成長は、あなたが着実に”数字”のスケールを行進していることを意味します。

以降と上向き

概念はよく知られているが、よく愛されていない場合、それは我々が我々の直感を構築する必要があることを意味します。 働く類推を見つけ、教科書が小走りするslopのために解決してはいけない。 私の頭の中で:

  • 対数は、効果の根本原因を見つける（成長、金利を見つける参照）
  • それらは、部分カウントのボーナスで乗算または桁を数えるのに役立ちます（500kは6.7桁の数)

幸せな数学。

このシリーズの他の投稿

  1. 指数関数への直感的なガイド&e
  2. 自然対数（ln）を分かりやすくする
  3. 単純、複合、連続金利への視覚的なガイド
  4. Eの一般的な定義（色付け）
  5. 理解指数（なぜ0^0=1なのですか？
  6. 実際の世界で対数を使う
  7. 指数と対数で考える方法
  8. 離散的な成長と連続的な成長の理解
  9. 指数は本当に何を意味しますか？
  10. Q:なぜeは特別なのですか？ (2.718…、2、3.7または別の番号ではありませんか？)