疫学の基礎
この章を読んだ後、次のことを行うことができます:
- 交絡因子と効果修飾子を区別する
- 層別分析を行い、効果修飾子がデータに存在するかどうかを判断します
前の章では、交絡について議論しました。 交絡因子は、適切に制御されていない場合、関連性の偏った推定につながる第三の変数です。 効果の変更には、第3の変数(露出ではなく、結果ではない)も含まれますが、この場合、絶対にそれを制御したくありません。 むしろ、効果修正の存在自体が興味深い発見であり、我々はそれを強調する。
効果修正(交互作用とも呼ばれます)が存在する場合、3番目の変数(共変数とも呼ばれます)のレベルごとに異なる結果が得られます。 たとえば、ある期間にわたってオレゴン州立大学(OSU)の学生の睡眠量とGPAに関するコホート研究を行うと、これらのデータを収集する可能性があります:
| GPA | |||
| < 3.0 | ≥ 3.0 | ||
| 睡眠の量 | < 8 時間 | 25 | 25 |
| > 8 時間 | 25 | 25 | |
これはコホート研究であったため、リスク比(RR)を計算します。:
睡眠量とその後のGPAとの間には関連性はありません。
これはコホート研究のリスク比であるため、時間枠を含める必要があります—私は”用語を終了する”と言っていました。 交絡の場合と同様に、これを未調整または粗RRと呼びます。
しかし、学生と話すことから、性別が重要な共変可能性であるかどうか疑問に思います。 交絡と同様に、我々は効果の修正をチェックするために層別分析を行うだろう。 繰り返しますが、同じ露出(睡眠)と結果(GPA)で2×2のテーブルを描画しますが、男性と女性のために別々のテーブルを描画します(性別は共変です)。 これを行うには、生データを振り返って、上記のA(E+、D+)セルの25人のうち、男性と女性の数を把握します。 <8時間を報告し、GPA<3を持っていた25人のうちとしましょう。0人、11人が男性、14人が女性であった。 次に、同様にB、C、およびDセルから参加者を分割し、層固有の2×2テーブルを作成します:
| 男性 | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| 睡眠の量 | < 8 時間 | 11 | 14 |
| 8+ 時間 | 17 | 9 | |
| 女性 | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| 睡眠の量 | < 8 時間 | 14 | 11 |
| 8+ 時間 | 8 | 16 | |
RRmen=\frac{(\frac{(\frac{(\frac{({11}{25})}{(\frac{17}{26})} = 0.68
RRwomen=\frac{(\frac{(\frac{(\frac{(\frac{{14}{25})}{(\frac{8}{24})} = 1.7
解釈:
男子学生のうち、一晩8時間未満の睡眠をとった人は、GPA<3の0.68倍のリスクを持っていました。期間の終わりに0、8時間以上を報告した人と比較して。
女子学生のうち、1泊8時間未満の睡眠をとった人は、学期末にGPA<3.0を発症するリスクが8時間以上報告された人と比較して1.7倍であった。
これらの仮説的なデータでは、8時間未満の睡眠は男子学生の間でGPAが高い(「結果」はGPAが低いため、1未満のRRは露出した個人がgpaが低い可能性が低いこ
この場合の性別は効果修飾子として機能しています:睡眠とGPAとの関連は共変量の地層によって異なります。 次のようにして、層別分析を行うときに効果の変更を見つけることができます:
- 関連の地層固有の措置が互いに異なっている
- 原油は、それらの間に落ちる
あなたが効果修正を持っている場合は、次のステップは、地層固有の措置 私たちは調整された尺度を計算しません(それは原油と同様に1.0近くになります); ここで興味深いのは、男性と女性が異なる睡眠に反応することです。 エフェクトの変更は、結果で強調したいものであり、調整するものではありません。
粗から調整されたものへの10%の変化が交絡のための受け入れられた定義である交絡のためのものとは異なり、層固有の尺度が何かを効果修飾子と呼 一度効果修飾子を宣言すると、その後、共変可能なレベルごとに結果を別々に報告する義務があるため、しきい値はおそらく交絡因子を宣言するのに必要なものよりも高くなければなりません。 したがって、疫学では、文献で報告された効果修正の証拠はめったに見られません。 長い話を短くすると、効果の変更のための十分な”異なる”は”明白に異なっています。”
記事を読むとき、効果の変更は時々相互作用と呼ばれるか、著者は層別分析を報告していると言うかもしれません。 これらの3つのフレーズのいずれかが、効果修飾子として機能する変数があるという手がかりです。
効果修正例II
2008年の住宅バブル景気後退(これが暴露)に続いて、米国経済は多くの雇用を失った。 ここでは、不況の前、中、および後に働いていた人々の数(結果)を示すグラフです。 結果は性別(共変量)によって階層化されて提示されており、分析者は性別が効果修飾子として機能している可能性があると疑っていることを意味し 実際、結果はわずかに異なります:男性(青)は雇用の割合が大きくなり、2014年の時点ではまだ景気後退前のレベルに回復していませんでしたが、女性(赤)は

ソース: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs
私たちも年齢別に層別にするとどうなりますか? まず、ここでは、不況が55歳以上の人々の仕事にどのように影響を与えたかを示すグラフがあります:
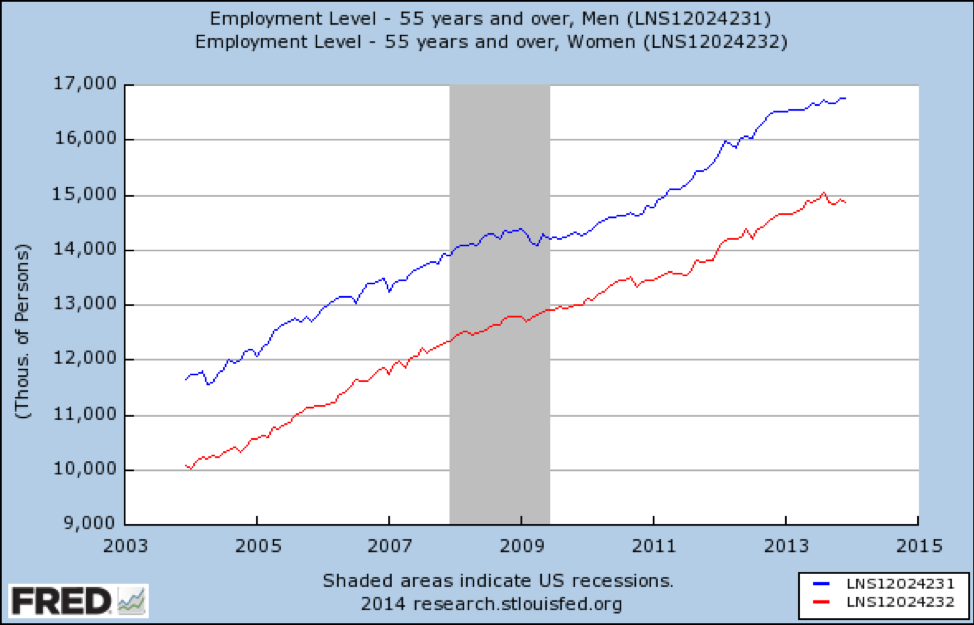
ソース: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt
景気後退は、古い働くアメリカ人にはまったく影響しませんでした。 また、性別による影響の修正も見られません—2つの線はほぼ平行です。
若い大人はどうですか?
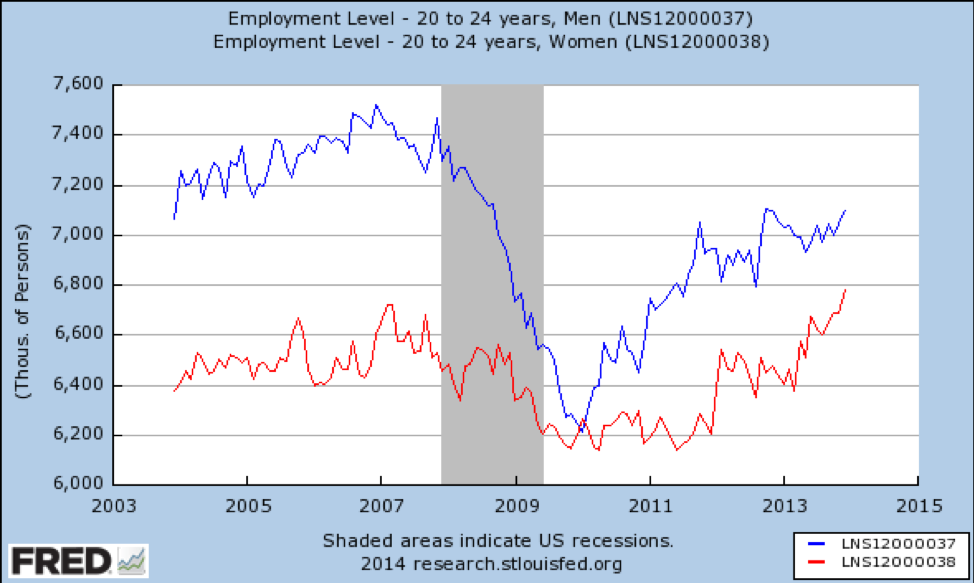
ソース: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv
ここでは、ジェンダーによる大きな影響の変更を持っている—若い男性は、利用可能な仕事の巨大な割合を失い、2014年の時点で完全に回復していませんでした。 不況は主に住宅バブルによって引き起こされ、建設労働者は主に若い男性であるため、これは驚くべきことではありません。 対照的に、若い女性は仕事のわずかな割合を失い、すぐに前職よりも優れたレベルに回復しました。
最後に、25歳から54歳までの求人を見てみましょう:
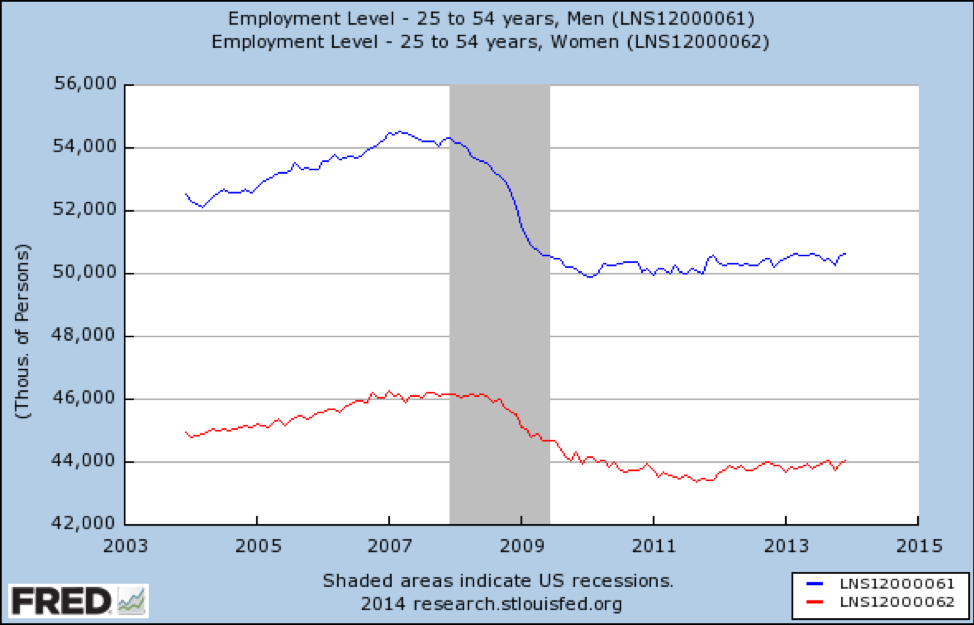
ソース: https://fred.stlouisfed.org/graph/?id=LNS12000061
ここでは、非常に荒涼とした写真を参照してください。 この年齢層では、女性よりも男性の方が仕事が失われ、2014の時点ではまったく回復していませんでした。
したがって、2008年の景気後退に対する雇用市場の対応を調べると、年齢による実質的な影響の変化(雇用の回復は年齢によって大幅に変化した)と、いくつかの年齢カテゴリー内では、性別による影響の変化の証拠も見られる。 雇用に対する景気後退の影響は、年齢や性別の異なる人々にとって異なっていた。
これは、政策の意味が非常に異なるため、重要です。 あなたが連邦政府の一員として働いていて、景気刺激策や回復策を設計しようとしていたと想像してください。 あなたが最初のグラフから来た唯一のデータで、年齢の内訳がない場合、潜在的な政策解決策は、年齢別の層別分析にもアクセスできる場合とは非常に異
交絡では、交絡因子がグループ間で均等に分散されていないため、最初は間違った答えを得ています。 これは、あなたが計算する関連付けの尺度を歪ませます(覚えておいてください:足を大きくすることは、学年レベルによって交絡するためにのみ読 そのため、代わりに、関連付けの尺度を再計算する必要があります。
効果修正では、最初は間違った答えを得ていますが、今回はサンプルに暴露/疾患関連が異なる少なくとも2つのサブグループが含まれているためです。 この場合、これらのサブグループを永続的に分離し、結果を報告する必要があります(これは他の共変数によって混同される場合とされない場合があ: この場合、睡眠が少ない男性は、睡眠が多い男性よりも高いGPAsを持っていますが、同時に、睡眠が多い女性は睡眠が少ない女性よりも高いGPAsを持ってい
ここでは、潜在的な交絡因子と効果修飾子を扱うためのプロセスを示す要約表です。 プロセスの多くは、あなたが持っている共変量のタイプに関係なく同じです(すべての場合において、あなたはあなたの研究中に共変量を測定し、そ). 差の領域は赤で示されています。
| 交絡 | 効果修正 | |
| 研究を計画する前に | 研究中の曝露/疾患プロセスについて知っていることに基づいて、どの変数が交絡因子として作用するかを考えてください。 | 研究中の曝露/疾患プロセスについて知っていることに基づいて、どの変数が効果修飾子として作用するかを考えてみてください。 |
| 研究中に | 潜在的な共変量に関するデータを収集する—共変量に関するデータなしでは成層/調整された分析を行うことはできません! | 潜在的な共変可能性に関するデータを収集する—共変可能性に関するデータなしでは、層別/調整された分析は実行できません! |
| 分析:ステップ1 | 関連性の粗測定値を計算します(共変量は無視します)。 | 関連性の粗測度を計算します(共変数は無視します)。 |
| 分析: ステップ2 | 共変数の各レベルが独自の2×2テーブルを持つように、関連の階層固有の尺度を計算します。 | 共変数の各レベルが独自の2×2テーブルを持つように、関連の階層固有の尺度を計算します。 |
| 分析:ステップ3 | 層固有の尺度が互いに類似しており、原油と少なくとも10%異なる場合(それらの間に収まらない)、共変数は交絡因子です。 | 層固有の測度が互いに異なり、粗値がそれらの間にある場合、共変量は効果修飾子になります。 |
| 書き込み結果 | 交絡因子を制御する関連付けの調整された尺度を報告します。 | 協会の層別対策を報告する。 |
高齢者の身体活動と認知症の横断的研究を行い、調整されていないオッズ比(OR)2.0を計算するとします。 婚姻状況は重要な共変量かもしれないと思うので、「現在結婚している」と「現在結婚していない」(結婚していない、離婚していない、未亡人を含む)で階層化し 現在結婚している人のORは3.1であり、現在結婚していない人のORは3.24です。 この場合、婚姻状況は交絡因子として機能しており、調整されたORを報告します(これは3.18程度になります)。
妊娠中の女性の早産を防ぐために、地中海の食事療法の無作為化試験を行うことを想像してみてください。 あなたは試行を行い、0.90のRRを計算します。 おそらくパリティは重要な共変可能性があると思うので、層別分析を行います。 未経産省のうち、RRは0.60であり、多経省のうち、RRは1.15である。 これらはお互いに異なっており、原油はそれらの間にあります。 この場合、パリティは効果修飾子として機能しているため、2つの層固有のRrを別々に報告します。
メラノーマおよび前の日焼けのベッドの使用の場合制御調査をしていることを想像しなさい。 原油ORは3.5ですが、おそらく性別は重要な共変です。 層別分析では、男性では3.45、女性では3.56のORが得られます。 この場合、共変数(性別)は交絡因子でも効果修飾子でもありません。 私たちは、(1)原油は2つの層固有の推定値の間にあるだけでなく、(2)層固有の推定値は原油と10%以下であるため、交絡因子ではないと言います。 私たちは、3.45と3.56はそれほど違いはないので、それは効果修飾子ではないと言います—どちらの場合も、実質的な効果(約3.5倍の高さ)があります。 性別の影響を説明するために調整も層別化も必要ないため、協会の粗見積もりを報告します。
はい! 通常、問題の共変数が連続変数であり、効果の変更を確認する目的で二分されている場合にこれが表示されます。 たとえば、年齢が効果修飾子であると思われる場合は、層別分析のためにサンプルを「古い」と「若い」に分割するかもしれません—たとえば、50歳以上対50歳以 51歳は70歳のようではないという程度に、我々は結果にいくつかの重要なニュアンスを欠場するかもしれません,おそらくデータに存在するため、より多 さらなる詳細はこの本の範囲を超えていますが、同じ共変数が理論的には交絡因子と効果修飾子の両方として機能することを知っていますが、実際にはこれを見ることはめったにありません。
結論
交絡とは異なり、その効果は我々の分析で取り除きたいが、効果の修正はそれ自体興味深い発見であり、我々はそれを報告する。 効果の修正を確認するには、層別分析を行います。 関連の層固有の尺度が互いに異なり、それらの間に粗雑なものがある場合、問題の変数が効果修飾子として機能している可能性があります。 共変量の層ごとに結果を個別に報告します。
一つの最後の、プット*イット*オール一緒にテーブル:
| これらがあなたのORs/Rrであれば: | ||||
| 層 | 層 | そして、共変は… | そして、あなたは報告するでしょう… | |
| 2.0 | 1.0 | 3.2 | 効果修飾子 | 関連の2つの層固有の措置 |
| 2.0 | 3.5 | 3.6 | 交絡計 | 調整された測度 |
| 2.0 | 1.9 | 2.0 | 何も面白くない | 原油メジャー |
研究における系統誤差(一部の人々はそれをバイアスと呼んでいます;私はしたくありません)は、曝露と疾患の関係を妨げる第三の変数によって引き起こ
暴露と結果との関係が第三の変数に基づいて変化するシナリオを指します。 例えば、おそらくヨガは女性ではなく、男性のACL傷害を防ぐことができます。 そのシナリオでのセックスは効果修飾子です。 効果の変更は交絡と同じではありません。
あなたの研究がそこにある何かを見つける確率。 Power=1-β;betaはタイプIIの誤り率です。 小規模な研究、またはまれなイベントの研究は、通常、電源が不足しています。
女性が何人の子供を持っていたか。 未経産女性(別名nuliparas)はまだ彼らの最初の子供を持っていない(彼らは妊娠しているかもしれないが、まだ子供を持っていない)、とparous女性は、少なくとも一つの前の子を持っていました。 多足類は少なくとも2人の前の子供を持っていた;初足類は1人の前の子供を持っていた。
これは女性の最初の妊娠です。
この女性には他の子供がいました。