隠されたマルコフモデル：単純な定義と概要

BY admin
|
上で共有

統計定義>

隠れマルコフモデル(HMM)は、順次データをモデル化する比較的簡単な方法です。 非表示のマルコフモデルは、データの基礎となるマルコフモデルが非表示または不明であることを意味します。 より具体的には、あなたは観測データだけを知っていて、状態に関する情報は知っていません。 言い換えれば、データを生成する特定のタイプのモデル（マルコフモデル）がありますが、どのプロセスがそれを生成しているのかわかりません。 基本的には、マルコフモデルの知識を使用して、モデルの構造についての教育を受けた推測を行います。

マルコフモデルとは何ですか？

隠されたマルコフモデルを明らかにするためには、まずマルコフモデルがそもそも何であるかを理解する必要があります。 サイコロと色のボールの袋：ここで私は確率で非常に精通している二つの項目を使用して簡単な例を作成します。


ランダムモデルの作成に使用するモデルコンポーネントは次のとおりです:

  • 六面赤ダイ。
  • 十面黒ダイ。
  • 十玉の赤い袋。 九つのボールは赤、一つは黒です。
  • 二十玉の黒い袋。 一つのボールは赤、十九は黒です。

“「黒」と「赤」は、このモデルの2つの状態です（つまり、黒にすることも、赤にすることもできます）。
次の手順でモデルを作成します。
隠しマルコフモデル

  1. 放出ステップ:ダイスを転がして下さい。 出てくる番号に注意してください。 これが発光です。 上の図では、私は（任意の—私は黒を選択している可能性があります）を開始するには、赤のダイを選択し、2をロールバックしました。
  2. 移行ステップ：ステップ1でロールしたダイスと一致する色のボールをバッグからランダムに選択します。 私は赤いダイスを転がしたので、私は赤い袋からボールを選ぶつもりです。 私は黒いボールを引き出したので、私は次の発光のために黒いダイに移行するつもりです。

その後、これらの手順を一定数の排出量まで繰り返すことができます。 たとえば、この一連のステップを10回繰り返すと、{2,3,6,1,1,4,5,3,4,1}というセットが得られます。 ある状態から次の状態に移行するプロセスは、マルコフプロセスと呼ばれます。


赤から黒または黒から赤への移行は、袋に黒と赤のボールの数が異なるため、異なる確率を運びます。 次の図は、2つの状態(黒と赤)を持つこの特定のモデルの確率を示しています):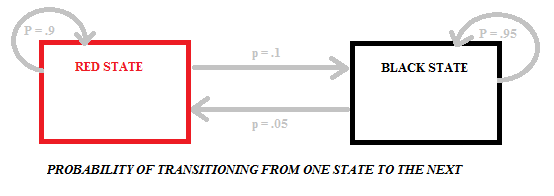

隠れマルコフモデル表記

ε=(A,B,ε)は、HMMの省略表記です。 隠れマルコフモデルでは、他の表記法が使用されています:

  • A=状態遷移確率(aij)
  • B=観測確率行列(bj(k))
  • N=モデル{1,2…N}内の状態の数または時間t→stの状態
  • M=状態ごとの異なる観測シンボルの数
  • Q={1,2…N}内の状態の数
  • Q={1,2…N}内の状態の数
  • Q={1,2…N}内の状態の数
  • Q={1,2…N}内の状態の数
  • Q={1,2…N}内の状態の数q0,q1,. . . ,qN−1}=マルコフ過程の異なる状態
  • T=観測シーケンスの長さ
  • V={0,1,. . . ,M-1}=可能な観測値のセット
  • O=(O0,O1,. . . 1)=観測シーケンス
  • λ=初期状態分布(ni)
  • s=状態または状態シーケンス(s1,s2…sn)
  • xk=隠れ状態
  • zk=観測。

三つの基本的な問題

三つの基本的な問題は、隠されたマルコフモデルで解決することができます:

  1. 隠れマルコフモデルΜ=(A,B,μ)と一連の観測値Oが与えられた場合、観測値P(O|μ)の確率を求めます。 これは評価問題と呼ばれることもあります。
  2. 隠れマルコフモデルΕ=(A,B,ε)と観測列Oが与えられたとき、最も可能性の高い状態列(s1,s2…sn)を求めます。 これは復号化問題と呼ばれることもあります。
  3. Oの確率を最大化する観測列(O1,O2…Onおよび隠れマルコフモデルμ=(A,B,μ)を求めます。

Rabiner,L.R.”a tutorial on hidden Markov models and selected applications in speech recognition”,Proceedings of THE IEEE,vol.77,pp.257-286,Feb. 1989.
Stamp,M.(2013). 隠されたマルコフモデルへの明らかな紹介。 取得8/6/2013から: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

“隠れマルコフモデル：単純な定義&の概要”からStatisticsHowTo.com：私たちの残りの部分のための基本的な統計！ https://www.statisticshowto.com/hidden-markov-model/

——————————————————————————

宿題やテストの質問の助けが必要ですか？ Cheggの調査を使うと、分野の専門家からのあなたの質問に段階的な解決を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です！