IIRフィルタとFIRフィルタの違い:実用的な設計ガイド

BY admin

| 10月 26, 2021

デジタルフィルタは、関心のある情報を抽出し、不要な情報を削除するために、デジタルデータセット(センサーデータなど)を操作する数学的アルゴリズムです。このタイプの技術の適用は、センサーデータからグリッチを取除くか、またはより容易なデータ分析のための測定された信号の騒音をきれいにするこしかし私達はいかに私達の適用のための最もよいタイプのデジタルフィルターを選ぶか。 IIRフィルタとFIRフィルタの違いは何ですか？

デジタルフィルタは、次の二つのカテゴリに分類されます:

無限インパルス応答(IIR)
有限インパルス応答(FIR)
有限インパルス応答(FIR))

名前が示すように、各タイプのフィルタは、そのインパルス応答の長さによって分類されます。ただし、詳細な数学的分析を開始する前に、各タイプのフィルターの性能と特性の違いを理解することをお勧めします。

例

IIRとFIRの違いを説明するために、14次のFIR(実線)と4次のチェビシェフI IIR(破線)の周波数応答を図1に示します。振幅スペクトルは同じ程度の減衰を持ちますが、IIRフィルターの位相スペクトルは通過帯域(\(\small0\rightarrow7.5Hz\))では非線形であり、カットオフ周波数\(\small f_c=7.5Hz\)では非常に非線形になることに注意してください。また、FIRでは、IIRの減衰特性に一致するために、より多くの係数（IIRの15対10）が必要であることにも注意してください。

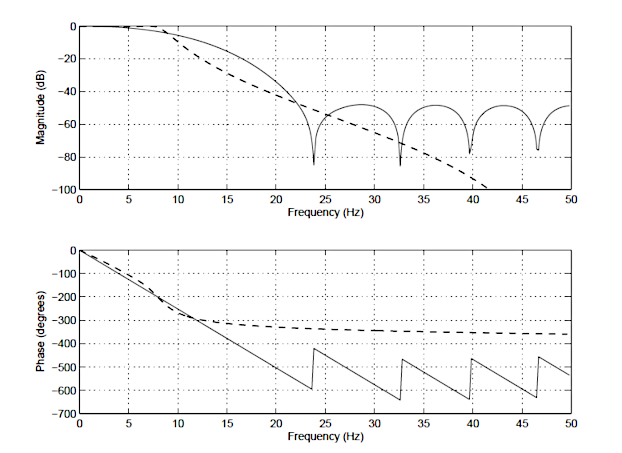
これらは、フィルタの二つのタイプの違いのほんの一部です。各タイプのフィルタの主な長所と短所の詳細な要約が次に続きます。

IIRフィルタ

IIR(infinite impulse response)フィルタは、一般的に線形位相があまり重要ではなく、メモリが制限されているアプリケーションに選択されます。それらは可聴周波等化、生物医学的なセンサーの信号処理、IoT/IIoTのスマートなセンサーおよび高速テレコミュニケーション/RFの適用で広く配置された。

利点

低実装コスト: 同様の仕様、すなわちカットオフ周波数と阻止帯域減衰を満たすために、FIRフィルタよりも少ない係数とメモリを必要とします。
低レイテンシ:係数の数が少ないため、リアルタイム制御および非常に高速なRFアプリケーションに適しています。
アナログ相当：s-z平面マッピング変換を使用してアナログフィルタの特性を模倣するために使用することができます。

非線形位相特性: ＩＩＲフィルタの位相特性は一般に非線形であり，特にカットオフ周波数付近では非線形である。通過帯域位相特性を改善するために、全通過等化フィルタを使用することができます。
より詳細な解析:固定小数点で実装すると、より多くのスケーリングと数値オーバーフロー解析が必要です。直接形態IIフィルター構造はquantisationの効果に特に敏感で、設計段階の間に特別な心配を要求する。
: フィードバック経路のために、それらのFIR（有限インパルス応答）の対応物よりも数値的に安定ではありません。

FIRフィルタ

fir(finite impulse response)フィルタは、一般に線形位相が重要であり、まともな量のメモリと計算性能が利用可能なアプリケーションに選択されます。それらに可聴周波および生物医学的な信号の強化の適用で広く配置されてがある。それらの全ゼロ構造（後述）は、いかなるタイプの入力信号に対しても不安定になることがないことを保証し、IIRよりも明確な利点を提供します。

利点

線形位相：Firは線形位相を持つように簡単に設計できます。これは、すべての周波数が同じ量だけ時間的にシフトされるため、フィルタリングされる信号に位相歪みが導入されないことを意味し、そのため、それらの相対的な高調波関係(すなわち、一定のグループと位相遅延)を維持します。これは、非線形位相特性を有するIIRフィルタでは確かに当てはまりません。
安定性：Firは現在の出力を計算するために以前の出力値を使用しないため、彼らはフィードバックを持っていない、彼らは彼らにIIRフィルタ上の明確な利点を与えるである入力信号の任意のタイプのために不安定になるこ
任意の周波数応答:Parks-McClellanおよびASN FilterScriptのfirarb()関数は、任意の振幅応答を持つFIRの設計を可能にします。これは、FIRをIIRよりも簡単にカスタマイズできることを意味します。
固定小数点性能:定量化の影響はIIRの影響よりも深刻ではありません。

: FIRsは通常、IIRの対応するものよりも鋭いカットオフを達成するために多くの係数を必要とします。その結果、はるかに多くのメモリと、より多くのMAC（複数および累積）操作が大幅に必要になることになります。しかし、ArmのCortex-Mコアをベースとした最新のマイクロコントローラアーキテクチャには、SIMD（信号命令、複数データ）を介したDSPハードウェアサポートが含まれており、フィル
より高いレイテンシ: 係数の数が多いほど、一般にFIRは高速で高スループットのアプリケーションにはIIRよりも適していません。これは、FIRフィルタがループ安定性を達成するには群遅延が多すぎる可能性があるリアルタイムの閉ループ制御アプリケーションで問題になります。
同等のアナログなし:双線形の整合z変換(s-zマッピング)を使用すると、アナログフィルタを同等のIIRフィルタに簡単に変換できます。ただし、同等のアナログを持たないため、これはFIRでは不可能です。

数学的定義

はじめに説明したように、IIRとFIRという名前は、各タイプのフィルタの数学的定義に由来しています。,

\(\displaystyle sum_{k=0}h{\infty}h(k)x(n-k)=\sum_{k=0}h{\infty}h(k)x(n-k)=\sum_{k=0}h{\infty}h(k)x(n-k)
\)

有限インパルス応答によって分類されるFIR,

\(\sum sum_{k=0}h{N-1}h(k)x(n-k)=\sum_{k=0}h{N-1}h(k)x(n-k)=\sum_{k=0}h{N-1}h(k)x(n-k)
\)

次に、各タイプのフィルタの数学的特性を順番に分析します。

IIRの定義

上記のように、IIRフィルタは理論的に無限のインパルス応答によって分類されます,

\(\実際には、この方程式を使用してIIRの出力を計算することはできません。\sum_{k=0}.{\infty}h（k）x（n-k）\）

したがって、方程式は、次のように与えられる線形定数係数差分方程式によって定義されるように、有限個の極\（\small p\）と零点\（\small q\）によって書き直すことがで:Y sum_{k=0}b{q}b_k x（n-k）-\sum_{k=1}a{p}a_ky（n-k）=\sum_{k=1}p{p}a_ky（n-k）=\sum_{k=1}p{p}a_ky（n-k）=\sum_{k=1}p{p}a_ky（n-k）=\sum_{k=1}q{p}a_ky（n-k）=\sum_{k=1)
\)

ここで、\(\small a_k\)と\(\small b_k\)は、フィルターの分母と分子の多項式係数であり、根はそれぞれフィルターの極と零点に等しくなります。したがって、差分方程式とｚ変換（伝達関数）との間の関係は、したがって、次のようなｚ変換遅延特性を使用することによって定義され得る。,

\(\displaystyle
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^{1+\sum\limits_{k=1}^p a_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^}}
\)

このように、伝達関数はフィルタの周波数領域表現です。また、出力データには極が作用し、入力データには零点が作用することにも注意してください。極は出力データに作用し、安定性に影響するため、BIBO（bounded input、bounded output）の安定性のために、その半径が単位円（つまり<1）の内側にとどまることが不可欠です。ゼロの半径はフィルターの安定性に影響しないため、あまり重要ではありません。これが、すべてゼロのFIR（有限インパルス応答）フィルタが常に安定している主な理由です。

BIBO安定性

線形時不変（LTI）システム（デジタルフィルタなど）は、すべての有界入力が有界出力を生じさせる場合、有界入力、有界出力安定、またはBIBO安定であると言われています。

\displaystyle\sum_{k=0}/{\infty}\left|h(k)\right|<\infty\)

ここで、\(\SMALL H(k)\)はltiシステムのインパルス応答です。この方程式を分析すると、システムのROC（収束領域）には単位円が含まれている必要があるため、システムの極が単位円の内側にある場合にのみ、BIBO安定性規準が満たされることが明らかになるはずです。したがって、すべての極が単位円の内側にある場合、有界入力信号は常に有界出力信号を生成すると言えば十分です。

一方、ゼロはこの要件によって制約されず、結果としてz平面上の任意の場所にある可能性があります。したがって、システム安定性解析は、最初に伝達関数の根（すなわち、分子多項式と分母多項式の根）を計算し、次に対応する極と零点をz平面上にプロットすることによって行うことができる。

システムは安定でも不安定でもないので、わずかに安定であると言われているので、単位円上にある極があれば興味深い状況が発生します。わずかに安定したシステムはBIBO安定ではありませんが、インパルス応答が正弦波を生成する簡単な方法を提供するため、デジタル発振器設計者によ

Biquad IIR filters

ここで説明するIIRフィルタの実装は、図2に示すように2つの極と2つの零点を持つため、biquadと呼ばれます。 Biquadの実装は、量子化と数値安定性の影響が最小限に抑えられるため、固定小数点の実装に特に便利です。ただし、biquad実装の全体的な成功は、利用可能な数精度に依存します。

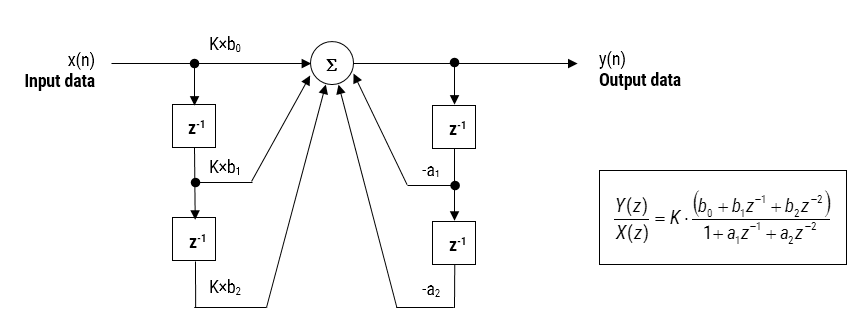
ダイレクトフォームI(biquad)IIRフィルタの実現と伝達関数。;ダイレクトフォーム;ビクワッドフィルター

図2:Direct Form I(biquad)IIRフィルタの実現と伝達関数

図2を分析すると、biquad構造は実際には2つのフィードバックパス（\(\small a_1\)と\(\small a_2\)でスケーリング）、3つのフィードフォワードパス（\(\small b_0,b_1\)と\(\small b_2\)でスケーリング）とセクショしたがって、図1のフィルタリング操作は、次の簡単な再帰式によって要約することができます:Displaystyle y（n）=K\times\Big–a_1y（n-1）-a_2y（n）yとすると、y a_1y（n-1）=A_2y（n-1）Kとなります。-2)\)

式を分析すると、biquadの実装に必要なのは4つの加算（アキュムレータを1つだけ必要とする）と5つの乗算だけで、どのCortex-Mマイクロコントローラでも簡単にセクションゲイン\(\small K\)は、実装前に順方向経路係数と事前に乗算することもできます。

Biquadフィルターのコレクションは、以下に示すようにBiquadカスケードと呼ばれます。

ASNフィルターデザイナーは、最大50個のbiquads(Professional editionのみ)のカスケードを設計および実装できます。

浮動小数点の実装

浮動小数点でフィルタを実装する場合(つまり、倍精度演算または単精度演算を使用する場合)、直接フォームII構造体は、直接フォームI構造体よりも優れた選択であると考えられています。直接形II転置構造は、差分方程式を分析することによって見られるように、数値スワンピングの望ましくない影響が最小限に抑えられるため、浮動小数点実装に最も数値的に正確であると考えられている。

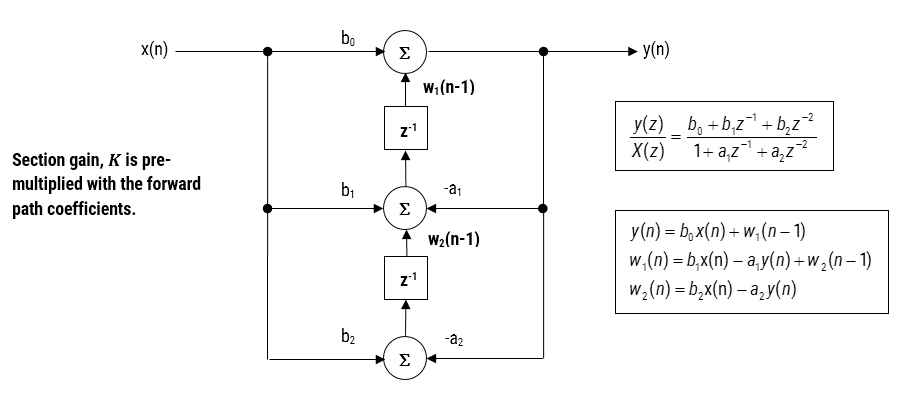
直接形II転置構造体、伝達関数および差分方程式;IIRフィルタ; ビクワッドフィルター

図3-Direct Form II Transposed strucutre,transfer function and difference equations

フィルタの概要(図4に示す)は、設計者に、技術仕様の詳細な概要とフィルタ係数を含む設計フィルタの詳細な概要を提供します。

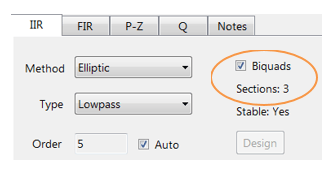
ASNフィルターデザイナーは、シングルセクションとBiquad(デフォルト設定)IIRフィルターの両方の設計と実装をサポートします。

図4:詳細な仕様。1246>

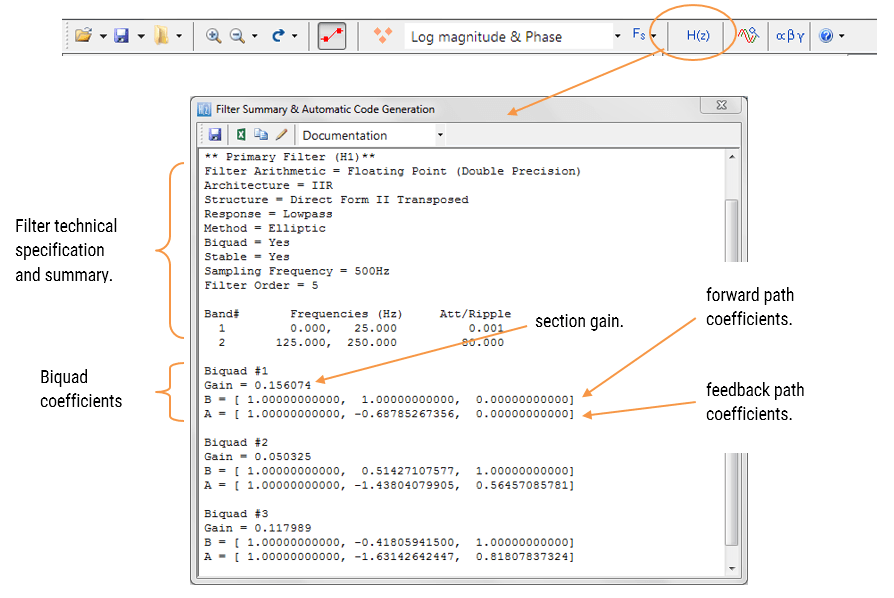
FIRの定義

IIRの線形定数係数差分方程式を返す、すなわち

\displaystyle
y(n)=\sum_{k=0}b{q}b_kx(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\sum_{k=1}a{p}a_ky(n-k)-\)
\)

\(\small a_k\)係数（すなわちフィードバック）をゼロに設定すると、定義は元のFIRフィルター定義に縮小されます。:Sum sum_{k=0}sum{q}b_kx（n-k）=\sum_{k=0}sum{q}b_kx（n-k）=\sum_{k=0}y{q}b_kx（n-k）=\sum_{k=0}y{q}b_kx（n-k）=\sum_{k=0})
\)

実装

FIRsのためのいくつかの実用的な実装が存在しますが、直接フォーム構造とその転置されたいとこがおそらく最も一般的に使用されており、そのため、すべての設計されたフィルタ係数は、直接フォーム構造での実装を意図しています。

直接形式の構造と関連する差分方程式を以下に示します。単一アキュムレータの概念によって固定小数点の実装のための直接形式が提唱されています。Y y（n）=b_0x（n）+b_1x（n-1）+b_2x（n-2）+……yとすると、y y（n）=b_0x（n）+b_1x（n-1）+b_2x（n-2）+……yとなります。 +b_qx(n-q) \)

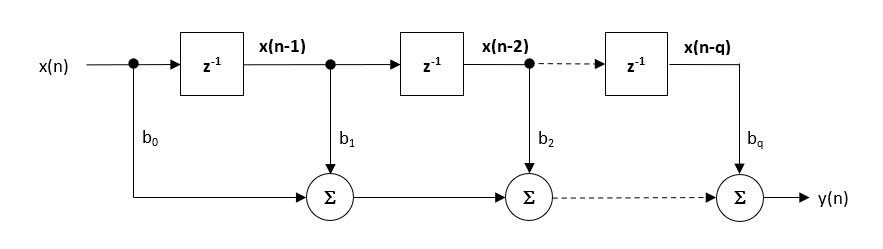
ASNフィルターデザイナー内で推奨される(デフォルトの)構造体はdirect Form Transposed構造体です。これは、浮動小数点加算が同様の大きさの数に対して実行されるため、数値スワンピングの望ましくない影響が最小限に抑えられるため、以下の差分方程式を分析することによって容易に見ることができます（実装に使用されます）。1922>

\(\displaystyle\begin{eqnarray}y(n)&=&b_0x(n)&+&w_1(n-1)\w_1(n)&=&b_1x(n)&+&w_2(n-1)\w_2(n)&=&b_1x(n)&+&w_2(n-1)\w_2(n)&=&b_1x(n)&+&w_2(n-1)\w_2(n)&=&b_1x(n)&+&B_2X（N）&+&W_3（N-1）\vdots\クワッド&=&\クワッド\vdots&+&\クワッド\vdots\W_Q（n）&=&B_QX（n）\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\end{eqnarray}\)

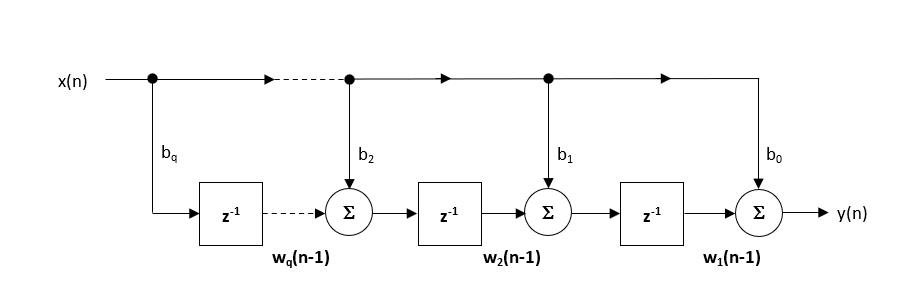
私たちは何を学んだのですか？