부트 스트랩 에 아르 자형

부트 스트랩은 샘플 데이터를 사용하여 모집단에 대한 추론 방법입니다.브래들리 에프론이 처음 소개했습니다.1979 년 종이.부트 스트랩은 샘플 데이터에서 대체 샘플링에 의존합니다. 이 기술은 통계의 표준 오차를 추정하는 데 사용할 수 있으며 신뢰 구간을 얻을 수 있습니다. 부트스트랩은 폐쇄된 폼이 없거나 매우 복잡한 폼이 있을 때 특히 유용합니다.

샘플이 있다고 가정 엔 요소:엑스={엑스 1,엑스 2,…,엑스 엔}그리고 우리는 씨에 대한 통계 티=티(엑스). 부트 스트랩 프레임 워크는 간단합니다. 우리는 단지 반복 아르 자형 시간 다음과 같은 계획:나는-번째 반복을 위해,대체 샘플 엔 사용 가능한 샘플에서 요소(그들 중 일부는 두 번 이상 선택 될 것입니다). 이 예제에서는 새 샘플이 부트스트랩 샘플이 아닌 부트스트랩 샘플이 아닌 부트스트랩 샘플이 아닌 부트스트랩 샘플이 아닌 부트스트랩 샘플이 아닌 부트스트랩 샘플을 호출할 수 있습니다.이 경우 통계 값은 다음과 같습니다. 우리는 그들을 호출 부트 스트랩 실현 의 티 또는 부트 스트랩 분포 의 티.그것을 기반으로,우리는 계산할 수 있습니다 씨…에 대한 티.이 작업을 수행하는 방법에는 여러 가지가 있습니다. 백분위 수를 취하는 것이 가장 쉬운 것 같습니다.

동작 중 부트 스트랩

잘 알려진iris데이터 세트를(다시 한번)사용합시다. 첫 번째 몇 행을 살펴보십시오.

중앙값Sepal.Length,중앙값Sepal.Width및 이들 사이의 스피어 맨의 순위 상관 계수에 대한 시스를 찾으려한다고 가정합니다. 우리는R의boot패키지와 호출 된 함수를 사용할 것입니다… boot. 그 힘을 사용하여 우리는 리샘플링 된 데이터에서 우리의 통계적(들)을 계산하는 함수를 만들어야합니다. dataset과 부트스트랩 샘플을 만들기 위해 선택한 데이터 집합의indices요소를 포함하는 벡터가 두 개 이상 있어야 합니다.

한 번에 둘 이상의 통계에 대해 시스를 계산하려면 함수를 단일 벡터로 반환해야 합니다.

예를 들어 다음과 같이 보일 수 있습니다:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo data에서 원하는 요소(숫자가indices에 저장되어 있음)를 선택하고 처음 두 열의 상관 계수를 계산합니다(method='s'은 스피어 맨의 순위 계수를 선택하는 데 사용되며method='p'은 피어슨의 계수로 발생합니다)및 중앙값.

몇 가지 추가 인수를 추가 할 수도 있습니다. 사용자가 유형 오드 상관 계수를 선택하게하십시오:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

이 자습서를보다 일반적으로 만들려면foo의 후자 버전을 사용합니다.

이제boot기능을 사용할 수 있습니다. 우리는 이름 오다 타셋,우리가 방금 만든 함수,반복 횟수(R)및 함수의 추가 인수(cor.type과 같은)를 제공해야합니다. 이하,이 예제의 재현성을 위해set.seed를 사용한다.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot 함수는 호출 된 클래스의 객체를 반환… (예,당신 말이 맞아!)boot. 두 가지 흥미로운 요소가 있습니다. $t부트스트랩 프로 시저(부트스트랩 실현)에 의해 생성 된 우리의 통계적 값을 포함합니다.):

$t0 원본,전체 데이터 집합에 통계 값을 포함합니다:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

콘솔에boot개체를 인쇄하면 몇 가지 추가 정보가 제공됩니다:

original $t0과 같습니다. bias은 부트 스트랩 실현($t의 평균)의 차이입니다.

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error 는 부트 스트랩 추정치의 표준 오류입니다.부트 스트랩 실현의 표준 편차와 같습니다.부트스트랩 구현의 배포를 살펴볼만한 가치가 있습니다. 우리는plot함수를 사용할 수 있으며index는foo에서 계산 된 통계 중 어느 것을보고 싶은지 알려줍니다. 여기서index=1는 양측 길이와 너비 사이의 창공의 상관 계수이고,index=2은 외경 꽃받침 길이의 중앙값이고,index=3는 외경 꽃받침 너비의 중앙값이다.

plot(myBootstrap, index=1)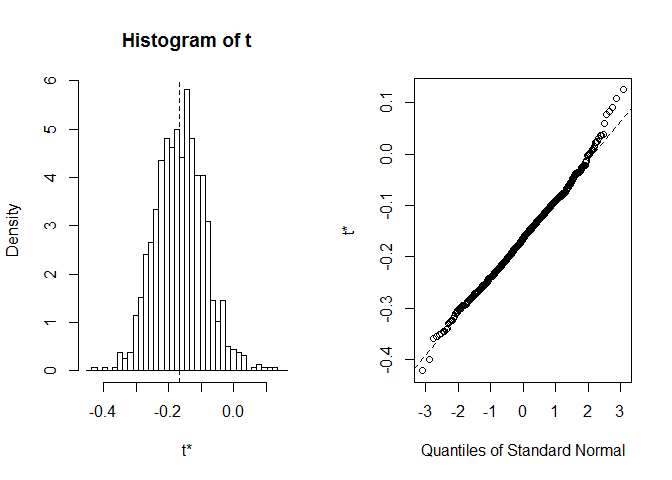

부트 스트랩 상관 계수의 분포는 꽤 보인다.정상적인 것과 같습니다. 그것을 위해 시를 찾아 보자. 우리는boot.ci을 사용할 수 있습니다. 하지만conf매개 변수를 사용하여 변경할 수 있습니다.

boot.ci5 가지 유형의 부트 스트랩 시스를 제공합니다. 그들 중 하나,학생간접,독특합니다. 부트 스트랩 분산을 추정해야합니다. 경고:bootstrap variances needed for studentized intervals를 인쇄합니다. 변형은 두 번째 수준의 부트 스트랩 또는(더 쉽게)잭 나이프 기술로 얻을 수 있습니다. 이 튜토리얼의 범위를 넘어 어떻게 든,그래서 부트 스트랩 시스의 나머지 네 가지 유형에 초점을 맞출 수 있습니다.

모두 보고 싶지 않으면type인수에서 관련 항목을 선택할 수 있습니다. 가능한 값은 다음과 같습니다norm, basic, stud, perc, bca 오라 이들의 벡터.

boot.ci함수는 클래스의 객체를 만듭니다… (예,당신은 짐작했습니다!)bootci. 그 요소는type인수에 사용되는 씨의 유형과 마찬가지로 호출됩니다. $norm은 신뢰 수준을 포함하는 3 요소 벡터입니다.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc 그리고$bca는 또한 계산하는 데 사용되는 백분위 수를 포함하는 5 요소 벡터입니다.):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

약간의 표기법(죄송합니다!(

)

(9347)

(9347)

(9347)

(9804) 그래서,하자:

• t 을 통한 수 bootstrap 견적(평균의 bootstraprealizations),
• t0 가치의 우리의 통계에서 원본 데이터 집합,
• se 통한 표준 오류의 부트스트랩 추정,
• b 것 바이어스의 부트스트랩 estimateb=t 적−t0
• α 신뢰 수준,일반적으로 α=0.95,
• za 수$1-\frac\알파 2$-quantile 의 standardnormal 배포,
• θα 수 α-백분율의 배급의 bootstraprealizations.1293>

백분위수 씨

위의 표기법으로 백분위수 씨입니다.:

(θ(1−α)/2,θ1−(1−α)/2)

그래서 이 다만 관련된 백분위. 아무것도 더.이 두 가지 주요 기능은 다음과 같습니다:

⋆

그러나 부트 스트랩의 경우,우리는 편견을 위해 그것을 수정해야합니다. 이 예제에서는 다음과 같이 설명됩니다.

$$티 0-티\\오후 알파\\\스타$$

기본 씨

백분위수 씨 일반적으로 수행이 좋지 않기 때문에 권장되지 않습니다.이상한 꼬리 분포에 관해서. 기본 씨(또한피부 또는 경험적 씨)는 이것에 훨씬 더 강력합니다. 각 부트스트랩 복제 및 티 0 사이의 차이를 계산하고 해당 분포의 백분위수를 사용하는 것이 합리적입니다. 8248>

(2 조−1 조−1 조)/2 조−1 조(1 조−1 조)/2 조−1 조(1 조-1 조)/2 조-1 조(1 조-1 조)/2 조-1 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조)/3 조(1 조))/2)

이 경우,상기 제 1 항은 제 2 항 및 제 2 항에서 제 2 항을 참조한다. 그만큼 공식 그것은 매우 복잡하지는 않지만 다소 직관적이지 않으므로 건너 뛸 것입니다.토마스 제이의 기사를 참조하십시오. 당신이 만약’세부 사항에 관심이 있다면.

메서드 이름에 언급 된 가속은 부트 스트랩 실현의 특정 비율을 사용해야합니다. 때로는 일어날 수 있습니다.이들은 극단적 인 백분위 수,아마도 이상치 일 것입니다.이러한 경우 비아그라가 불안정 할 수 있습니다.

꽃잎 너비 중앙값에 대해 살펴 보겠습니다. 원래 데이터 세트에서 이 중앙값은 정확히 3 입니다.우리는 2.9,2.9 를 얻습니다. 이상하지만 운 좋게도R은extreme order statistics used as endpoints라고 경고했습니다. 여기서 정확히 무슨 일이 일어 났는지 보자:

plot(myBootstrap, index=3)

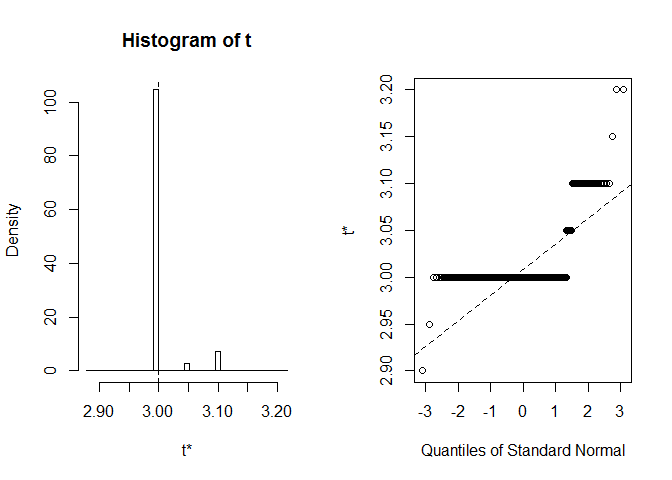
부트스트랩 실현의 분포는 드문 경우입니다. 그들 중 대다수(90%이상)는 3 초입니다.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

결과 복제

때때로 부트 스트랩 복제를 다시 작성해야합니다. 우리가 그것을 위해R을 사용할 수 있다면,이것은 문제가되지 않습니다. set.seed기능이 문제를 해결합니다.다른 소프트웨어에서 부트 스트랩 복제를 다시 만드는 것은 훨씬 더 어려울 것입니다. 또한 큰 연구의 경우R의 재 계산도 옵션이 될 수 없습니다(예:시간 부족으로 인해).

우리는 각각의 부트 스트랩 샘플을 형성 원본 데이터 세트의 요소의 인덱스를 저장,이 문제를 처리 할 수 있습니다. 이것은boot.array함수(indices=T인수 포함)가 수행하는 것입니다.

tableOfIndices<-boot.array(myBootstrap, indices=T)

각 행은 하나의 부트스트랩 샘플입니다. 예.,우리의 첫 번째 샘플은 다음과 같은 요소를 포함

설정indices=F(기본값),우리는 질문에 대한 답을 얻을 것이다”어떻게원래 데이터 세트의 각 요소는 각 부트 스트랩 샘플에 등장 여러 번?”. 예를 들어,첫 번째 샘플에서: 데이터 세트의 첫 번째 요소가 나타 났을 때 두 번째 요소가 전혀 나타나지 않았고 세 번째 요소가 한 번,네 번째 요소가 두 번 나타났습니다.

이와 같은 테이블을 사용하면R외부에서 부트 스트랩 실현을 다시 만들 수 있습니다.또는R자체에서set.seed를 사용하고 모든 계산을 다시 한 번하고 싶지 않을 때.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

결과가 동일한지 확인해 봅시다:

예,그렇습니다!

머신러닝에 대해 더 알고 싶으시다면,데이터캠프의 머신러닝 툴박스 과정을 수강하세요.