Bootstrap I R
Bootstrap er en metode for slutning om en populasjon ved hjelp av eksempeldata.Bradley Efron introduserte det først i dettepapir i 1979.Bootstrap er avhengig av prøvetaking med erstatning fra eksempeldata. Denne teknikken kan brukes til å estimere standardfeilen til enhver statistikk og toobtain et konfidensintervall (KI) for det. Bootstrap er spesielt nyttignår CI ikke har en lukket form, eller den har en svært komplisert.
Anta at vi har et utvalg av n-elementer: X = {x1, x2,…, xn} og weare interessert I CI for noen statistikk T = t (X). Bootstrapframework er grei. Vi gjentar Bare r ganger følgendeordningen: for i-th repetisjon, prøve med erstatning n elementer fratilgjengelig prøve (noen av dem vil bli plukket mer enn en gang). Kall thisnew sample i-th bootstrap sample, Xi, og calculatedesired statistikk Ti = T (Xi).
som et resultat får Vi r-verdier av vår statistikk: T1, T2,…, TR. Vi kaller dembootstrap realiseringer Av T eller en bootstrap distribusjon Av T. Basert på det, kan vi beregne CI For T. det er flere måter å gjøre dette på. Å ta prosentiler synes å være den enkleste.
Bootstrap i aksjon
La oss bruke (igjen) kjente iris datasett . Ta en titt på en første rad:
Anta at vi vil finne CIs for median Sepal.Length, median Sepal.Width og Spearmans rangkorrelasjonskoeffisient mellom thesetwo. Vi bruker R‘s boot pakke og en funksjon kalt… boot. For å bruke sin kraft må vi lage en funksjon som beregner ourstatistic (s) ut av resampled data. Den skal ha minst toargumenter: en dataset og en vektor som inneholder indices elementer fra et datasett som ble plukket for å lage en bootstrap-prøve.
hvis Vi ønsker å beregne CIs for mer enn en statistikk samtidig, må ourfunction returnere dem som en enkelt vektor.
for vårt eksempel kan det se slik ut:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo velger ønskede elementer (hvilke tall er lagret i indices) fra data og beregner korrelasjonskoeffisient av de to første kolonnene (method='s' brukes til å velge Spearmans rangkoeffisient,method='p' vil resultere med Pearsons koeffisient) og deres medianer.
Vi kan også legge til noen ekstra argumenter, f.eks. la brukeren velge type odcorrelation coefficient:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )} For å gjøre denne opplæringen mer generell, bruker jeg den siste versjonen avfoo.
nå kan vi bruke boot – funksjonen. Vi må levere det med et navn oddataset, funksjon som vi nettopp har opprettet, antall repetisjoner (R) og eventuelle ekstra argumenter for vår funksjon(som cor.type). Nedenfor Bruker jeg set.seed for reproduserbarhet av dette eksemplet.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funksjonen returnerer et objekt av klassen som kalles… (ja, du har rett !)boot. Den har to interessante elementer. $t inneholder r verdier av ourstatistic (s) generert av bootstrap prosedyre (bootstrap realiseringer ofte):
$t0 inneholder verdier av vår statistikk (er) i original, full, datasett:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000Utskrift boot objekt til konsollen gir ytterligere informasjon:
original er det samme som $t0. bias er en forskjell mellom gjennomsnittet av bootstrap realiseringer (de fra $t), kalt en bootstrap estimateof T Og verdi i opprinnelige datasett(den fra $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error er en standard feil av bootstrap estimat, som equalsstandard avvik av bootstrap realiseringer.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414Ulike typer bootstrap CIs
før VI begynner MED CI, er det alltid verdt å ta en titt pådistribusjon av bootstrap realiseringer. Vi kan bruke plot funksjon, medindex å fortelle hvilken statistikk beregnet i foo vi ønsker å se. Her er index=1 En Spearmans korrelasjonskoeffisient mellom sepal lengde og bredde, index=2 er en median od sepal lengde, ogindex=3 er en median od sepal bredde.
plot(myBootstrap, index=1)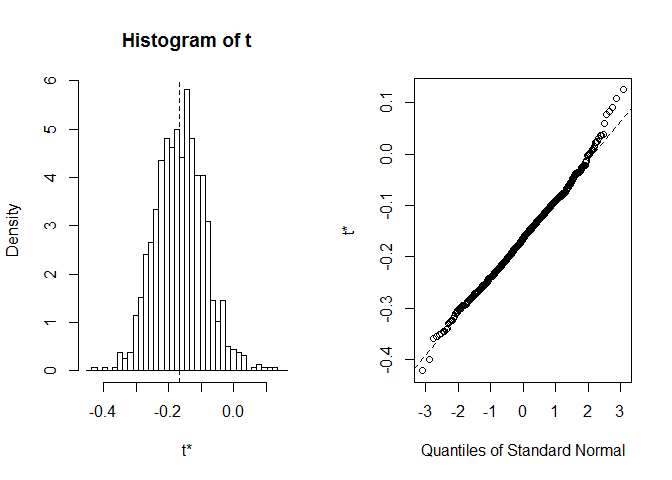
Fordelingen av bootstrap korrelasjonskoeffisienter virker ganskenormal-lignende. La OSS finne CI for det. Vi kan bruke boot.ci. Det standard to95 prosent CIs, men det kan endres med parameteren conf.
boot.ci gir 5 typer bootstrap CIs. En av dem, studentizedinterval, er unik. Den trenger et estimat av bootstrap varians. Vi gir det ikke, så R skriver ut en advarsel:bootstrap variances needed for studentized intervals. Varianceestimates kan fås med andre nivå bootstrap eller (enklere) withjackknife teknikk. Dette er liksom utenfor rammen av denne opplæringen, så la oss fokusere på de resterende fire typer bootstrap CIs.
hvis vi ikke vil se dem alle, kan vi velge relevante i type argument. Mulige verdier er norm, basic, stud, perc, bca ora vektor av disse.
funksjonen boot.ci oppretter objekt av klasse… (ja, du har gjettet!)bootci. Dens elementer kalles akkurat som TYPER CI brukt i typeargument. $norm er en 3-element vektor som inneholder confidence leveland CI grenser.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc og $bca er 5-elementvektorer som inneholderogså prosentiler som brukes til å beregne CI (vi kommer tilbake til dette senere):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178Litt av notasjon (Beklager!)
For å få en følelse av hva forskjellige TYPER CI er, må vi introdusere litt notasjon. Så, la:
- t⋆ være bootstrap-estimatet (gjennomsnitt av bootstraprealizations),
- t0 være en verdi av vår statistikk i det opprinnelige datasettet,
- se⋆ være en standard feil av bootstrap-estimatet
- b være en skjevhet av bootstrap estimateb = t⋆ − t0
- α være et konfidens nivå, vanligvis α = 0.95,
- za være en $1-\frac \alpha 2$-kvantil av standardnormal distribusjon,
- θα være en α-persentilen i fordelingen av bootstraprealizations.
Persentil KI
med ovennevnte notasjon er persentil KI:
så dette tar bare relevante prosentiler. Ikke noe mer.
Normal KI
et Typisk WALD KI ville være:
men i bootstrap-saken bør vi rette det for bias. Så blir det:
$$t_0 – b \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star $ $
Grunnleggende CI
Persentil CI anbefales vanligvis ikke fordi Det fungerer dårlignår det kommer til rare-tailed distribusjoner. Basic CI (også kaltpivotal eller empirisk CI) er mye mer robust til dette. Den rationalebak det er å beregne forskjeller mellom hver bootstrap replikasjonog t0 og bruke persentiler av deres distribusjon. Fullstendige detaljer kan bli funnet, for eksempel I L. Wassermans allestatistikk
Endelig formel for grunnleggende CI er:
BCa CI
BCa kommer fra bias-korrigert, akselerert. Formulafor det er ikke veldig komplisert, men litt unintuitive, så jeg hopper over det.Se Artikkel Av Thomas J. DiCiccio og BradleyEfron hvis du er interessert i detaljer.
Akselerasjon nevnt i metodens navn krever bruk av spesifikke percentiler av bootstrap-realiseringer. Noen ganger kan det skje thatthese ville være noen ekstreme persentiler, muligens uteliggere.BCa kan være ustabil i slike tilfeller.
La oss se På BCa CI for petal bredde median. Inoriginal datasett er denne medianen lik nøyaktig 3.
vi får BCa CI (2.9, 2.9). Det er rart ,men heldigvis Radvarte oss om det extreme order statistics used as endpoints. La oss sehva skjedde akkurat her:
plot(myBootstrap, index=3)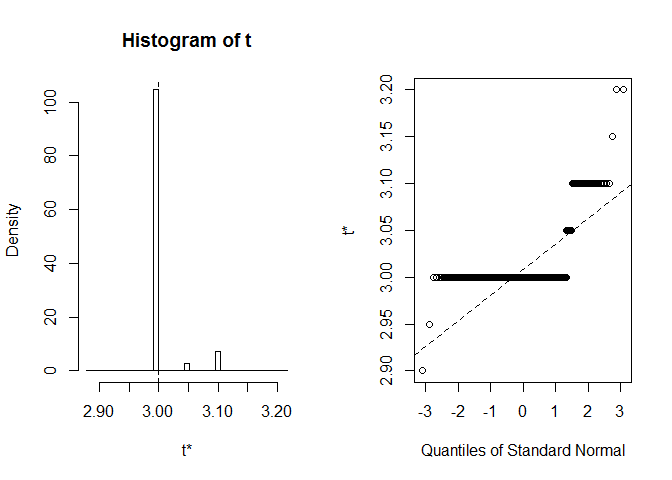
Distribusjon av bootstrap realiseringer er uvanlig. Et stort flertall av dem (over 90%) er 3s.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2Replikering av resultater
noen ganger må vi gjenskape bootstrap-replikasjoner. Hvis vi kan bruke Rfor det, er dette ikke et problem. set.seed funksjonen løser problemet.Å gjenskape bootstrap-replikasjoner i annen programvare ville være mye morecomplisert. Hva mer er, for stor R, kan omberegning i R ogsåikke være et alternativ (på grunn av mangel på tid, for eksempel).
Vi kan håndtere dette problemet, lagre indekser av elementer av originaldataset, som dannet hver bootstrap-prøve. Dette er hva boot.array funksjon (med indices=T argument) gjør.
tableOfIndices<-boot.array(myBootstrap, indices=T)Hver rad er en bootstrap-prøve. F. eks., vår første prøve inneholder følgende elementer:
Innstilling indices=F(en standard), vi får svar på spørsmålet «Howmany ganger hvert element av originalt datasett dukket opp i hver bootstrapsample?». For eksempel, i den første prøven: det 1ste elementet i datasettet dukket opp en gang, 2. element ble ikke vist i det hele tatt, 3. element dukket opp en gang, 4thtwice og så videre.
et bord som dette tillater oss å gjenskape bootstrap realisering utenfor R.Eller i R selv når vi ikke vil bruke set.seed og gjøre all thecomputation igjen.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')la oss sjekke om resultatene er de samme:
ja, det er de!
hvis Du ønsker Å lære Mer Om Maskinlæring I R, ta Datacamps Machine Learning Toolbox kurs.