Bruke Logaritmer I Den Virkelige Verden

Logaritmer er overalt. Noen gang bruke følgende setninger?

• 6 tall
• doble sifre
• størrelsesorden
• Rente

du beskriver tall i form av deres krefter på 10, en logaritme. Og en rente er logaritmen til veksten i en investering.

Overrasket over at logaritmer er så vanlige? Jeg også. De fleste forsøk På Matematikk I Den Virkelige Verden (TM) peker på logaritmer i noen arcane formel, eller late som om vi er geologer fascinert av Richters Skala. «Forskere bryr seg om logger, og du bør også. Også, kan du forestille deg en verden uten sink?»

Nei, nei, nei, nei, nei! (Mamma mia!)

Math uttrykker begreper med notasjon som » ln «eller » log». Å finne «matte i den virkelige verden» betyr å møte ideer i livet og se hvordan de kunne skrives med notasjon. Ikke se etter de bokstavelige symbolene! Når skrev du sist et skilt? Når var siste gang du hakket opp litt mat?

Ok, ok, vi får det: hva handler logaritmer om?

Logaritmer finner årsaken til en effekt, dvs.inngangen for noen utdata

en vanlig «effekt» ser noe vokse, som å gå fra \ $ 100 til \ $150 om 5 år. Hvordan skjedde dette? Vi er ikke sikre, men logaritmen finner en mulig årsak: en kontinuerlig avkastning på ln(150/100) / 5 = 8,1% vil utgjøre den endringen. Det kan ikke være den faktiske årsaken (skjedde all veksten i det siste året?), men det er et jevnt gjennomsnitt vi kan sammenligne med andre endringer.

forresten er begrepet «årsak og virkning» nyansert. Hvorfor er 1000 større enn 100?

• 100 er 10 som vokste av seg selv i 2 tidsperioder ($10 * 10$)
• 1000 er 10 som vokste av seg selv i 3 tidsperioder ($10 * 10 * 10$)

vi kan tenke på tall som utganger (1000 er «1000 utganger») og innganger («Hvor mange ganger trenger 10 å vokse for å lage disse utgangene?»). Så,

1000 outputs > 100 outputs

fordi

3 inputs > 2 inputs

Eller med andre ord:

log(1000) > log(100)

Hvorfor er dette nyttig?

Logaritmer setter tall på en menneskelig skala.

Store tall bryter hjernen vår. Millioner og billioner er «virkelig store» selv om en million sekunder er 12 dager og en trillion sekunder er 30.000 år. Det er forskjellen mellom En Amerikansk ferie år og helheten av menneskelig sivilisasjon.

trikset for å overvinne «stort tallblindhet» er å skrive tall i form av «innganger» (dvs.deres kraftbase 10). Denne mindre skalaen (0 til 100) er mye lettere å forstå:

• kraft av 0 = $10^0$ = 1 (enkelt element)
• strøm av 1 = $10^1$ = 10
• kraft på 3 = $10^3$ = tusen
• kraft på 6 = $10^6$ = millioner
• kraft på 9 = $10^9$ = milliarder
• kraft på 12 = $10^12$ = billioner
• kraft på 23 = $10^23$ = antall molekyler i et dusin gram karbon
• kraft på 80 = $10^80$ = antall molekyler i universet

en skala fra 0 til 80 tok oss fra et enkelt element til antall ting i universet. Ikke så shabby.

Logaritmer teller multiplikasjon som trinn

Logaritmer beskriver endringer i form av multiplikasjon: i eksemplene ovenfor er hvert trinn 10x større. Med den naturlige loggen er hvert trinn » e » (2.71828…) ganger mer.

når du arbeider med en rekke multiplikasjoner, logaritmer hjelpe «telle» dem, akkurat som tillegg teller for oss når effekter er lagt til.

Vis meg matematikken

tid for kjøttet: la oss se hvor logaritmer dukker opp!

Sekssifret lønn eller 2-sifret utgift

vi beskriver tall i form av deres sifre, dvs. hvor mange krefter på 10 har de (er de i tiere, hundrevis, tusenvis, titusener, etc.). Å legge til et siffer betyr «multiplikasjon med 10», dvs.

Logaritmer teller antall multiplikasjoner lagt til, så starter med 1 (et enkelt siffer) vi legger til 5 flere sifre ($10^5$) og 100 000 får et 6-talls resultat. Å snakke om » 6 «i stedet for» hundre tusen » er essensen av logaritmer. Det gir en grov følelse av skala uten å hoppe inn i detaljer.

Bonusspørsmål: Hvordan vil du beskrive 500 000? Å si «6 figur» er misvisende fordi 6-tall ofte innebærer noe nærmere 100.000. Ville» 6.5 figur » fungere?

Egentlig ikke. I hodene våre betyr 6,5 «halvveis» mellom 6 og 7 figurer, men det er en adder tankegang. Med logaritmer a».5 » betyr halvveis i form av multiplikasjon, dvs. kvadratroten ($9^.5$ betyr kvadratroten av 9-3 er halvveis i form av multiplikasjon fordi den er 1 til 3 og 3 til 9).

Ved å ta logg (500 000) får vi 5,7, legg til 1 for det ekstra sifferet, og vi kan si » 500 000 er en 6.7 figur nummer». Prøv det her:

størrelsesorden

vi geeks elsker denne setningen. Det betyr omtrent «10x forskjell», men høres bare kulere enn «1 siffer større».

i datamaskiner, hvor alt regnes med biter (1 eller 0), har hver bit en doblingseffekt (ikke 10x). Så går fra 8 til 16 biter er «8 størrelsesordener» eller $2^8 = 256$ ganger større. («Storre» i dette tilfellet refererer til mengden minne som kan adresseres.) Å gå fra 16 til 32 bits betyr en ekstra 16 størrelsesordener, eller $2^16 $ ~ 65 536 ganger mer minne som kan adresseres.

Renter

Hvordan finner vi vekstrater? Et land har ikke tenkt å vokse med 8,56% per år. Du ser PÅ BNP ett år OG BNP det neste, og ta logaritmen for å finne den implisitte vekstraten.

Mine to favorittfortolkninger av den naturlige logaritmen (ln (x)), dvs. 1.5:

• Forutsatt 100% vekst, hvor lenge trenger du å vokse for å komme til 1.5? (.405, mindre enn halvparten av tidsperioden)
• Forutsatt 1 tidsenhet, hvor fort trenger du å vokse for å komme til 1,5? (40.5% per år, kontinuerlig sammensatt)

Logaritmer er Hvordan vi finner ut hvor fort vi vokser.

Måleskala: Google PageRank

Google gir hver side på nettet en poengsum (PageRank) som er et grovt mål på autoritet / betydning. Dette er en logaritmisk skala, som i hodet mitt betyr «PageRank teller antall siffer i poengsummen din».

så et nettsted med pagerank 2 («2 siffer») er 10x mer populært enn Et PageRank 1-nettsted. Min side Er PageRank 5 OG CNN har PageRank 9, så det er en forskjell på 4 størrelsesordener ($10^4$ = 10,000).

Grovt sett får jeg omtrent 7000 besøk / dag. Ved hjelp av konvoluttmatningen kan JEG gjette AT CNN får ca 7000 * 10 000 = 70 millioner besøk / dag. (Hvordan gjorde jeg det? I hodet mitt tror jeg $7k * 10k = 70 * k * k = 70 * m$). De kan ha noen ganger mer enn DET (100M, 200M), men sannsynligvis ikke opp TIL 700M.

Google formidler mye informasjon med en svært grov skala (1-10).

Måleskala: Richter, Decibel, etc.

Sukk. Vi er på typiske «logaritmer i den virkelige verden» eksempel: Richters skala og Decibel. Tanken er å sette hendelser som kan variere drastisk (jordskjelv) på en enkelt skala med et lite område (vanligvis 1 til 10). Akkurat Som PageRank, er hver 1-punkts økning en 10x forbedring i kraft. Det største menneskeskapte jordskjelvet var 9,5; Yucatá – halvøya, som sannsynligvis gjorde dinosaurene utryddet, var 13.

Desibel er like, selv om Det kan være negativt. Lyder kan gå fra intenst stille (pindrop) til ekstremt høyt (fly) og hjernen vår kan behandle alt. I virkeligheten er lyden av en flymotor millioner (milliarder, trillioner) ganger kraftigere enn en pindrop, og det er ubeleilig å ha en skala som går fra 1 til en gazillion. Logger holder alt på en rimelig skala.

Logaritmiske Grafer

du vil ofte se elementer plottet på en «log scale». I hodet mitt betyr dette at den ene siden teller «antall sifre» eller «antall multiplikasjoner», ikke selve verdien. Igjen, dette bidrar til å vise vilt varierende hendelser på en enkelt skala(går fra 1 til 10, ikke 1 til milliarder).

Moores lov er et godt eksempel: vi dobler antall transistorer hver 18. måned (bilde høflighet Wikipedia).

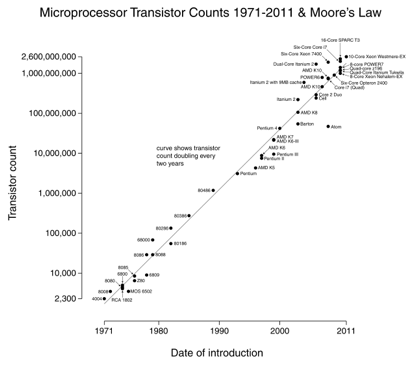
den fine tingen om log-skala grafer er eksponentielle endringer (prosessorhastighet) vises som en rett linje. Å vokse 10x per år betyr at du stadig marsjerer opp» sifre » skalaen.

Videre og oppover

hvis et konsept er kjent, men ikke elsket, betyr det at vi må bygge vår intuisjon. Finn analogier som fungerer, og ikke betale for slop en lærebok vil trave ut. I hodet mitt:

• Logaritmer finner grunnårsaken til en effekt (se vekst, finn rente)
• de hjelper med å telle multiplikasjoner eller sifre, med bonusen på delvise teller (500k er et 6,7 sifret tall)

Glad matte.

Andre Innlegg I Denne Serien

1. En Intuitiv Guide Til Eksponentielle Funksjoner & e
2. Demystifying Den Naturlige Logaritmen (ln)
3. En Visuell Guide Til Enkle, Sammensatte Og Kontinuerlige Renter
4. Vanlige Definisjoner av e (Farget)
5. forstå eksponenter (hvorfor betyr 0^0 = 1?)
6. Bruke Logaritmer I Den Virkelige Verden
7. Hvordan Tenke Med Eksponenter Og Logaritmer
8. Forstå Diskret vs. Kontinuerlig Vekst
9. hva betyr en eksponent egentlig?
10. Q: Hvorfor er e spesiell? (2.718…, ikke 2, 3,7 eller et annet nummer?)