En Sirkel er jevnt delt inn i seks like trekanter
Hei Marilynn,
Først vil jeg fortelle deg mine forutsetninger om hvordan bildet ditt ser ut:
- hver trekant har et toppunkt (hjørne) i midten av sirkelen
- Hver trekant har hjørner på omkretsen av sirkelen (så to sider av hver trekant er en radius)
- trianglene deler sider (det er ingen gapes mellom trekanter)
det overordnede bildet ser ut som en blomst – hver trekant er et kronblad.

det ukjente området er det som er igjen rundt utsiden av sirkelen, mellom omkretsen og utsiden av hver trekant. Dette ukjente området er delt inn i seks kongruente seksjoner(lik på alle måter – som trekantene er «like» på alle måter-inkludert område, lengde på side og buelengde). Det er ikke klart om du mener at arealet av en bue Er Pi (ikke egentlig delt Kake, selv om det er det samme), eller alle seks seksjonene sammen Er Pi. I det følgende vil jeg anta at en av de utvendige seksjonene har Et Område Av Pi, slik at arealet av alle seks seksjonene sammen er 6 Ganger Pi. Vi må finne radiusen til sirkelen, ring den r.
jeg vil også bruke P til Å stå For Pi(eller ca. 3.14). Nå er det mye informasjon vi kan garnere fra trekanter:
- vinklene i midten er alle 60 grader. Dette skyldes at de seks vinklene i midten er alle like, og en sirkel har 360 grader. Så gjør 360 edivided av 6.
- Hver trekant er Ensidig. Dette skyldes at to sider er like (sidene som er en radius).
- Hver trekant, er faktisk likesidet. Fordi det er iscoceles, er de to utvendige vinklene også like. Men det er 180 grader i en trekant, 60 er allerede brukt i midtvinkelen,og gir 180-60 = 120 grader for utvendige vinkler. Men 120 delt med 2 er 60 grader, så alle tre vinkler er like, så det er isoscles.
- Hver side i hver trekant er av lengde r. Dette skyldes at vi har 6 kongruente («like» på alle måter) like-sidige trekanter, og fordi to sider av hver trekant er en radius.
fra geometrien til trekantene må vi gjøre litt algebra. Fordi vi kjenner et område, og vi trenger en radius, trenger vi en formel (eller ligning) for radius når det gjelder område (i det som følger, hold målet med en formel i tankene). Arealet av sirkelen Er P*r2 (r2 betyr r kvadrat, og * betyr multipliser) arealet av de resterende seksjonene utenfor trekantene, men inne i sirkelen (et område vi allerede ikke er 6 * P), kan også bli funnet ved å trekke arealet av trekantene fra sirkelområdet. Vi må finne et område av en av de like-sidige trekanter.
Metode 1 for å beregne et område av en trekant
arealet av en trekant er b * h / 2 Det er her noe trigonometri er nødvendig: Tegn en linje fra et toppunkt til en motsatt side som deler motsatt side i halv og er i rette vinkler. Dette deler den like-sidige trekanten i to kongruente rettvinklede trekanter, og den nye siden er høyden, kaller den h. vi må finne h.
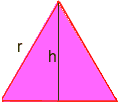
Ved å Bruke trig i en av de rette vinklede trekanter har vi sin60 = h/r, men sin60 = sqr(3)/2, hvor sqr (3) betyr kvadratroten av tre så sqr(3)/2 = h/r multipliser begge sider med r for å få h = r*sqr (3)/2 R Nå er arealet av en like-sidig trekant b*h/2 = (r)*(r * sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6 * sqr(3)/4)) Bruk rekkefølgen av operasjoner for å beregne på en kalkulator (Med P=3,14): r= 5,896… Så er radiusen til sirkelen ca. 5.9. Paul