Forskjellen Mellom IIR og FIR filtre: en praktisk design guide

et digitalt filter er en matematisk algoritme som opererer på et digitalt datasett (f. eks sensordata) for å trekke ut informasjon av interesse og fjerne uønsket informasjon. Anvendelser av denne typen teknologi, inkluderer å fjerne glitches fra sensordata eller til og med rydde opp støy på et målt signal for enklere dataanalyse. Men hvordan velger vi den beste typen digitalt filter for vår søknad? Hva er forskjellen mellom ET IIR-filter og ET FIR-filter?

Digitale filtre er delt inn i følgende to kategorier:

• Uendelig impulsrespons (IIR)
• Endelig impulsrespons (FIR)

som navnene antyder, er hver type filter kategorisert etter lengden på impulsresponsen. Men før du begynner med en detaljert matematisk analyse, er det forsiktig å sette pris på forskjellene i ytelse og egenskaper for hver type filter.

Eksempel

for å illustrere forskjellene mellom EN IIR og GRAN, er frekvensresponsen til en 14. ordens GRAN (heltrukket linje) og en 4.ordens Chebyshev type I IIR (stiplet linje) vist nedenfor i Figur 1. Legg merke til at selv om størrelsesspektrene har en lignende grad av demping, er fasespektret til IIR-filteret ikke-lineært i passbåndet (\(\small 0 \ rightarrow7. 5Hz\)), og blir veldig ikke-lineært ved avskjæringsfrekvensen, \(\small f_c=7.5 Hz\). Legg også merke til AT FIR krever et høyere antall koeffisienter (15 vs IIRS 10) for å matche dempningsegenskapene til IIR.

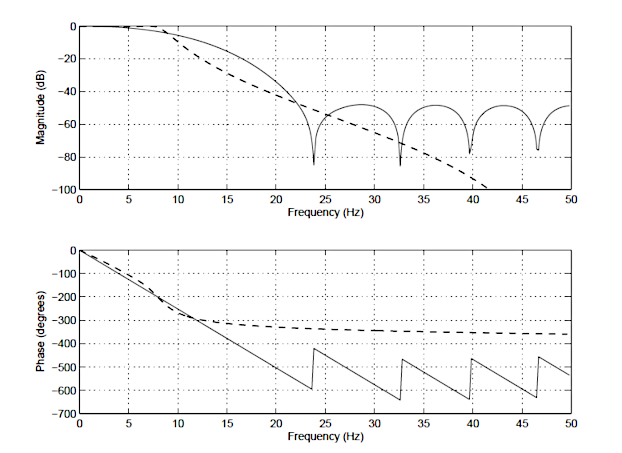
Dette er bare noen av forskjellene mellom de to typer filtre. En detaljert oppsummering av de viktigste fordelene og ulempene ved hver type filter vil nå følge.

iir-filtre

iir (infinite impulse response) – filtre er vanligvis valgt for applikasjoner der lineær fase ikke er for viktig og minnet er begrenset. De har vært mye brukt i lydutjevning, biomedisinsk sensorsignalbehandling,iot / iiot smarte sensorer og høyhastighets telekommunikasjon/RF-applikasjoner.

Fordeler

• Lav implementeringskostnad: krever mindre koeffisienter og minne enn FIR filtre for å tilfredsstille et lignende sett med spesifikasjoner, dvs. cut-off frekvens og stopband demping.
• Lav latens: egnet for sanntidskontroll OG SVÆRT høyhastighets RF-applikasjoner i kraft av det lave antallet koeffisienter.
• Analog ekvivalent: Kan brukes Til å etterligne egenskapene til analoge filtre ved hjelp av s – z plane mapping transforms.

Ulemper

• ikke-lineære faseegenskaper: Fase charactersitics av EN IIR filter er generelt ikke-lineære, spesielt nær cut – off frekvenser. All-pass utjevningsfiltre kan brukes for å forbedre passbåndets faseegenskaper.
• Mer detaljert analyse: Krever mer skalering og numerisk overflyt analyse når implementert i fast punkt. Direct form II-filterstrukturen er spesielt følsom for effekten av kvantisering, og krever spesiell forsiktighet i designfasen.
• Numerisk stabilitet: Mindre numerisk stabil enn DERES FIR (finite impulse response) kolleger, på grunn av tilbakemeldingsbanene.

FIR filtre

FIR (finite impulse response) filtre er vanligvis valgt for applikasjoner der lineær fase er viktig og en anstendig mengde minne og beregningsytelse er tilgjengelig. De har en utbredt bruk i lyd-og biomedisinske signalforbedringsprogrammer. Deres null-struktur (diskutert nedenfor) sikrer at de aldri blir ustabile for noen form for inngangssignal, noe som gir dem en klar fordel over IIR.

Fordeler

• Lineær fase: FIRs kan enkelt utformes for å ha lineær fase. Dette betyr at ingen faseforvrengning innføres i signalet som skal filtreres, da alle frekvenser forskyves i tid med samme mengde – og dermed opprettholder deres relative harmoniske forhold (dvs.konstant gruppe og faseforsinkelse). Dette er absolutt ikke tilfelle med iir-filtre, som har en ikke-lineær fasekarakteristikk.
• Stabilitet: Som FIRs bruker ikke tidligere utdataverdier til å beregne deres nåværende utgang, dvs. de har ingen tilbakemelding, de kan aldri bli ustabile for alle typer inngangssignal, noe som gir dem en klar fordel over IIR-filtre.
• Vilkårlig frekvensrespons: Parks-McClellan Og ASN Filterscripts firarb () – funksjon tillater utformingen av EN GRAN med en vilkårlig størrelsesrespons. DETTE betyr at EN GRAN kan tilpasses lettere enn EN IIR.
• Fast punktytelse: effektene av kvantisering er mindre alvorlige enn for EN IIR.

Ulemper

• høy beregnings-og minnekrav: FIRs krever vanligvis mange flere koeffisienter for å oppnå en skarp cut-off enn sine iir-kolleger. Konsekvensen av dette er at de krever mye mer minne og betydelig en høyere MENGDE MAC (flere og akkumulere) operasjoner. Men moderne mikrokontrollerarkitekturer basert på Arms Cortex-M-kjerner inkluderer NÅ dsp-maskinvarestøtte via SIMD (signal instruction, multiple data) som fremskynder filtreringsoperasjonen betydelig.
• Høyere latens: jo høyere antall koeffisienter, betyr at GENERELT EN GRAN er mindre egnet enn EN IIR for rask høy gjennomstrømning applikasjoner. Dette blir problematisk for sanntids lukket-loop kontroll programmer, der EN FIR filter kan ha for mye gruppe forsinkelse for å oppnå loop stabilitet.
• ingen analog ekvivalent: Ved Hjelp Av Bilinær, matchet z-transform( s-z-kartlegging), kan et analogt filter enkelt omdannes til et tilsvarende iir-filter. Dette er imidlertid ikke mulig for EN GRAN som den ikke har noen analog ekvivalent.

Matematiske definisjoner

som omtalt i innledningen, kommer navnet IIR og FIR fra de matematiske definisjonene av hver type filter, dvs. et iir-filter er kategorisert ved sin teoretisk uendelige impulsrespons,

\(\displaystyle
y (n)=\sum_{k = 0}^{\infty}h (k)x (n-k)
\)

og EN GRAN kategorisert av sin endelige impulsrespons,

Vi vil nå analysere de matematiske egenskapene til hver type filter i sin tur.

iir-definisjon

som vist ovenfor er et iir-filter kategorisert ved sin teoretisk uendelige impulsrespons,

\(\displaystyle y (n)=\sum_{k=0}^{\infty}h (k) x (nk)\)

Praktisk talt er det ikke mulig å beregne utgangen av EN IIR ved hjelp av denne ligningen. Derfor kan ligningen skrives om i form av et endelig antall poler \(\liten p\) og nuller \(\liten q\), som definert av den lineære konstante koeffisientdifferansekvasjonen gitt av:

\(\displaystyle
y (n)= \ sum_{k = 0}^{q}b_k x(nk)-\sum_{k=1}^{p}a_ky (nk)
\)

hvor, \(\small a_k\) og \(\small b_k\) er filterets nevneren og teller polynom koeffisienter, som har røtter er lik filterets poler og nuller henholdsvis. Dermed kan et forhold mellom differanseligningen og z-transformasjonen (overføringsfunksjonen) derfor defineres ved å bruke z-transformasjonsforsinkelsesegenskapen slik at,

\(\displaystyle
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}}{1 + \ sum \ limits_{k=1}^p a_kz^{- k}}
\)

som sett er overføringsfunksjonen en frekvensdomenerepresentasjon av filteret. Legg også merke til at polene virker på utgangsdataene og nullene på inngangsdataene. Siden polene virker på utgangsdataene og påvirker stabiliteten, er det viktig at radiene forblir inne i enhetssirkelen (dvs. <1) for BIBO (begrenset inngang, begrenset utgang) stabilitet. Radiene til nullene er mindre kritiske, da de ikke påvirker filterstabiliteten. Dette er den primære grunnen til at all-zero FIR (finite impulse response) filtre alltid er stabile.

bibo stabilitet

et lineært tidsinvariant (lti) system (slik som et digitalt filter) sies å være avgrenset inngang, avgrenset utgang stabil, ELLER BIBO stabil, hvis hver avgrenset inngang gir opphav til en avgrenset utgang, som

\(\displaystyle \sum_{k=0}^{\infty}\venstre|h(k)\høyre|<\infty \)

hvor, \(\liten h(k)\) er LTI-systemets IMPULSRESPONS. Ved å analysere denne ligningen bør DET være klart AT BIBO stabilitetskriteriet bare vil bli oppfylt dersom systemets poler ligger inne i enhetssirkelen, siden systemets ROC (konvergensregion) må inkludere enhetssirkelen. Følgelig er det tilstrekkelig å si at et begrenset inngangssignal alltid vil produsere et begrenset utgangssignal hvis alle polene ligger inne i enhetssirkelen.

nullene derimot, er ikke begrenset av dette kravet, og som en konsekvens kan ligge hvor som helst på z-planet, siden de ikke direkte påvirker systemstabiliteten. Derfor kan en systemstabilitetsanalyse utføres ved først å beregne røttene til overføringsfunksjonen (dvs.røtter av teller-og nevnerpolynomene) og deretter plotte de tilsvarende polene og nullene på z-planet.

en interessant situasjon oppstår hvis noen poler ligger på enhetssirkelen, siden systemet sies å være marginalt stabilt, da det ikke er stabilt eller ustabilt. Selv om marginalt stabile systemer ikke ER BIBO stabile, har de blitt utnyttet av digitale oscillatordesignere, siden deres impulsrespons gir en enkel metode for å generere sinusbølger, som har vist seg å være uvurderlig innen telekommunikasjon.

Biquad IIR-filtre

iir-filterimplementeringen som er omtalt her, sies å være biquad, siden den har to poler og to nuller som illustrert nedenfor i Figur 2. Biquad-implementeringen er spesielt nyttig for faste punktimplementeringer, da effekten av kvantisering og numerisk stabilitet minimeres. Den samlede suksessen til enhver biquad-implementering er imidlertid avhengig av tilgjengelig tallpresisjon, som må være tilstrekkelig nok for å sikre at de kvantiserte polene alltid er inne i enhetssirkelen.

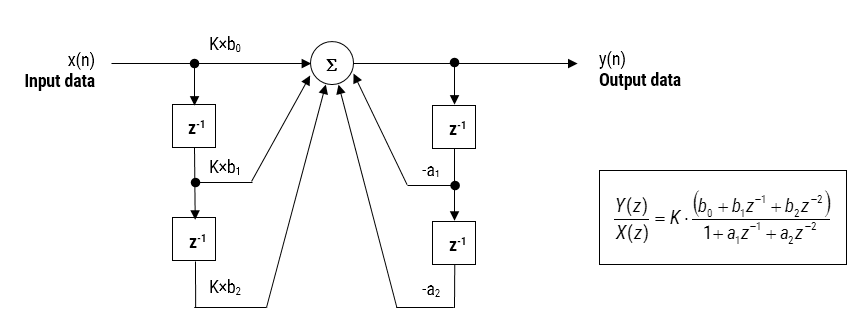
Figur 2: Direkte Form I (biquad) iir filter realisering og overføring funksjon.

Ved Å Analysere Figur 2 Kan man se at biquad-strukturen faktisk består av to tilbakemeldingsbaner (skalert med \(\small a_1\) og \(\small a_2\)), tre feed forward-baner (skalert med \(\small b_0, b_1\) og \(\small b_2\)) og en seksjonsgevinst, \(\small K\). Dermed kan filtreringsoperasjonen Av Figur 1 oppsummeres ved følgende enkle rekursive ligning:

\(\displaystyle y(n)=K\ganger\Stor – A_1 y(n-1) – a_2 y (n-2)\)

Analysere ligningen, legg merke til at biquad-implementeringen bare krever fire tillegg (krever bare en akkumulator) og fem multiplikasjoner, som lett kan innkvarteres på En Hvilken som Helst Cortex-m mikrokontroller. Seksjonsgevinsten, \(\liten K\) kan også forhåndsmultipliseres med fremoverbanekoeffisientene før implementering.

en samling av biquad filtre er referert til Som En Biquad Kaskade, som illustrert nedenfor.

ASN Filter Designer kan designe og implementere en kaskade på opptil 50 biquads (Kun Professional edition).

flyttallsimplementering

Ved implementering av et filter i flyttall (dvs. ved bruk av dobbel eller enkel presisjonsaritmetikk) Anses Direkte Form II-strukturer å være et bedre valg enn Direkte Form I-strukturen. Den Direkte Form II Transponerte strukturen anses som den mest numerisk nøyaktige for flyttallsimplementering, da uønskede effekter av numerisk swamping minimeres som sett ved å analysere differansekvasjonene.

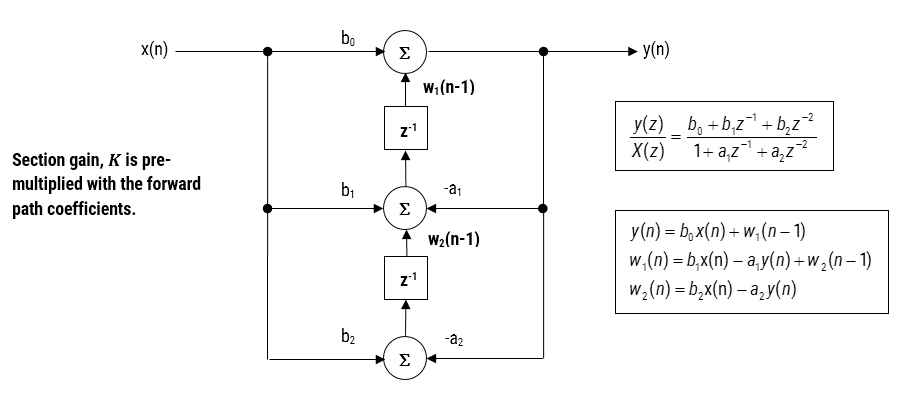
Figur 3-Direkte FORM II Transponert strucutre, overføring funksjon og forskjell ligninger

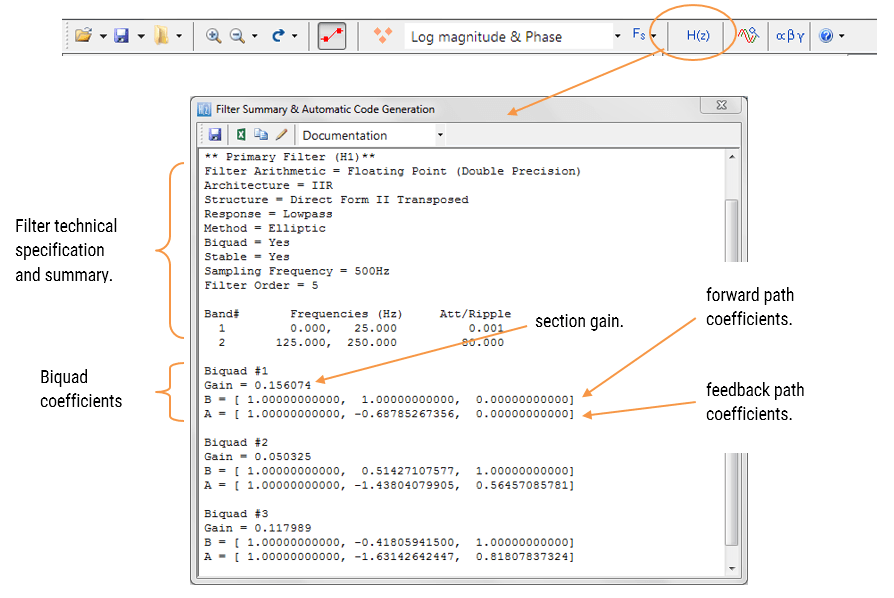
filteret sammendrag (vist i Figur 4) gir designeren med en detaljert oversikt over designet filteret, inkludert en detaljert oppsummering av de tekniske spesifikasjonene og filter koeffisienter, som presenterer en rask og enkel rute for å dokumentere design.

ASN Filter Designer støtter design og implementering av både enkelt seksjon OG Biquad (standardinnstilling) iir filtre.

Figur 4: detaljert spesifikasjon.

FIR definisjon

Returnerer IIRS lineære konstante koeffisientforskjellligning, dvs.

\(\displaystyle
y(n)=\sum_{k=0}^{q}b_kx(nk)-\sum_{k=1}^{p}a_ky (nk)
\)

legg merke til at når vi setter \(\small a_k\) koeffisientene (dvs. tilbakemeldingen) til null, reduserer definisjonen TIL vår opprinnelige FIR filterdefinisjonen, noe som betyr AT FIR-beregningen bare er basert på tidligere og nåværende inngangsverdier, nemlig:

\(\displaystyle
y (n)=\sum_{k = 0}^{q}b_kx(n-k)
\)

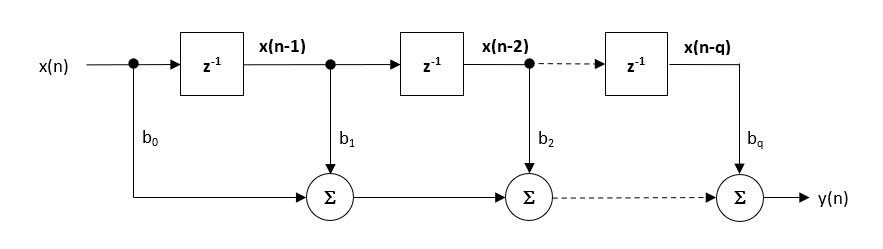
Implementering

Selv om flere praktiske implementeringer for FIRs eksisterer, er den direkte formstrukturen og dens transponerte fetter kanskje den mest brukte, og som sådan er alle utformede filterkoeffisienter ment for implementering I En Direkte formstruktur.

Den Direkte formstrukturen og tilhørende forskjell ligning er vist nedenfor. Den Direkte Formen er orde for fast punkt implementering i kraft av enkelt akkumulator konseptet.

\(\displaystyle y (n) = b_0x ( n) + b_1x (n-1) + b_2x (n-2)+…. +b_qx(n-q)) \)

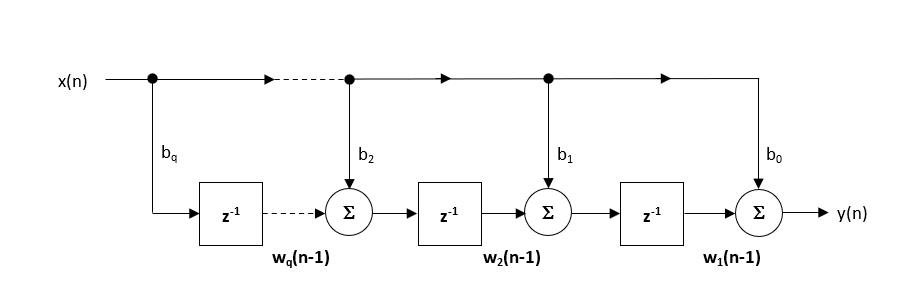
den anbefalte (standard) strukturen i ASN Filter Designer Er Direkte Form Transponert struktur, da dette gir overlegen numerisk nøyaktighet ved bruk av flyttall aritmetikk. Dette kan lett sees ved å analysere forskjellen ligninger nedenfor (brukt for implementering), som uønskede effekter av numerisk swamping er minimert, siden flyttall addisjon utføres på tall av tilsvarende størrelse.

\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)

Hva har vi lært?

Digitale filtre er delt inn i følgende to kategorier:

• Uendelig impulsrespons (IIR)
• Endelig impulsrespons (FIR)

iir (infinite impulse response) filtre er vanligvis valgt for applikasjoner der lineær fase ikke er for viktig og minne er begrenset. De har vært mye brukt i lydutjevning, biomedisinsk sensorsignalbehandling,iot / iiot smarte sensorer og høyhastighets telekommunikasjon/RF-applikasjoner.

FIR (finite impulse response) filtre er vanligvis valgt for applikasjoner der lineær fase er viktig og en anstendig mengde minne og beregningsytelse er tilgjengelig. De har en utbredt bruk i lyd-og biomedisinske signalforbedringsprogrammer.

ASN Filter Designer gir ingeniører med alt de trenger for å designe, eksperimentere og distribuere komplekse IIR og FIR digitale filtre for en rekke sensor måling programmer. Disse fordelene kombinert med automatisk dokumentasjon og kodegenereringsfunksjonalitet tillater ingeniører å designe og validere et iir/FIR digitalt filter i løpet av minutter i stedet for timer.