KDnuggets

Av Sydney Firmin, Alteryx.

«I Hovedsak er alle modeller feil, men noen modeller er nyttige.»- George Box

Dette berømte George Box-sitatet ble først registrert i 1976 i papiret «Science And Statistics», publisert I Journal Of American Statistical Association. Det er et viktig sitat til feltet av statistikk og analytiske modeller og kan pakkes ut i to deler.

Alle Modeller Er Feil

for å grave inn i denne uttalelsen må vi definere og undersøke hva en modell er.

for konteksten til denne artikkelen kan en modell betraktes som en forenklet representasjon av et system eller objekt. Statistiske modeller tilnærmer mønstre i et datasett ved å gjøre antagelser om dataene, samt miljøet det ble samlet inn og brukt på.

de tre brede kategoriene av antagelser gjort av statistiske modeller er fordelingsforutsetninger (antagelser om fordeling av verdier i en variabel eller fordelingen av observasjonsfeil), strukturelle forutsetninger (antagelser om det funksjonelle forholdet mellom variabler) og kryssvariasjonsforutsetninger (felles sannsynlighetsfordeling).

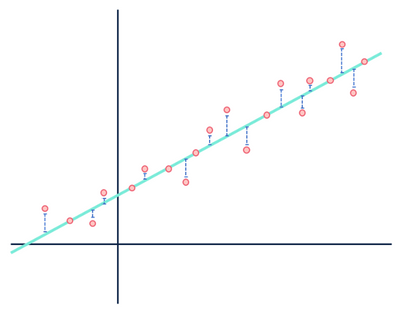
for eksempel antar en lineær regresjonsmodell at relasjonene mellom variabler i et datasett er lineære (og bare lineære). I øynene til en lineær modell er enhver avstand mellom observasjonene som utgjør datasettet og den modellerte linjen bare støy (dvs. tilfeldige eller uforklarlige svingninger i dataene) og kan til slutt ignoreres.

Betal ikke tankene til avstandene i blått.

George Box uttalte at alle modeller er feil spesielt i sammenheng med statistiske modeller. Fordi selve naturen til en modell er en forenklet og idealisert representasjon av noe, vil alle modeller være feil på en eller annen måte. Modeller vil aldri være «sannheten» hvis sannheten betyr helt representativ for virkeligheten. Det er svært viktig å vurdere forutsetningene i å generere en modell fordi modellene er bare virkelig nyttig når forutsetningene holdes opp.

Kart Og Miniatyrer

Lignende observasjoner Til Box ‘ s «all models are wrong» finnes på mange ulike felt.

Det er en aforisme som refererer til kartterritoriet, tilskrevet Alfred Korzybski:

et kart er ikke territoriet det representerer, men hvis det er riktig, har det en lignende struktur til territoriet, som står for bruken.

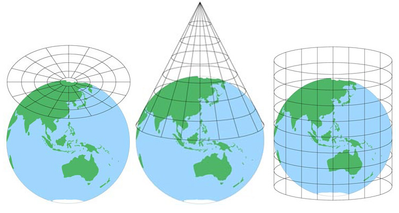
Kart er nyttige fordi De er abstraksjoner av et reelt objekt i en mer håndterlig skala, men de vil alltid utelukke noe detaljnivå. Avhengig av hvor mye område et kart inneholder, kan det også være noen forvrengning på grunn av projeksjonen av kartet (forårsaket av den vanskelige prosessen med å konvertere en sfærisk globus til en flat representasjon).

(Bildekilde.)

det eneste virkelig nøyaktige kartet ville være en 1: 1 replikering av territoriet det representerer. Men et kart som det ville ikke være mer nyttig enn å navigere selve territoriet.

Tenk på sitatet Fra poeten Paul Valery:

alt enkelt er falskt. Alt som er komplekst er ubrukelig.

Oppkalt etter En Stanford business professor, Beskriver Bonini Paradox utfordringen med å skape nyttige, komplette modeller eller simuleringer av komplekse systemer. Det er ofte en balansegang mellom kompleksitet og nøyaktighet i modellutvikling. Hvis målet med en modell er å gjøre et forhold eller system klarere, slår økt kompleksitet det formålet (selv om det kan gjøre modellen mer nøyaktig).

på et høyt nivå beskriver map-territory-relasjonen også forholdet mellom et objekt og en representasjon av objektet.

hvis du noen gang har tatt en filosofiklasse, har du kanskje kommet over arbeidet Forræderiet Av Bilder av surrealistiske kunstneren Rene Magritte.

teksten oversetter til » Dette er ikke et rør.»Og det er det ikke. Vi kan ikke kaste dette (digitale) bildet med tobakk og røyke det som det bare er en representasjon av et ekte objekt.

Modeller er abstraksjoner. Som kart, eller miniatyr arkitektoniske modeller eller skjemaer, kan de ikke fange opp alle detaljer i objektet eller systemet de er basert på, om bare fordi de ikke eksisterer i den virkelige verden og ikke fungerer på samme måte.

Hvis Alle Modeller Er Feil, Hvorfor Bry Deg?

George Box aforisme er ikke uten sine kritikere.

problemet mange statistikere har med dette sitatet synes å grovt faller inn i to kategorier:

1. Modeller som er feil er en åpenbar uttalelse. Selvfølgelig er alle modeller feil, de er modeller.
2. dette sitatet brukes som en unnskyldning for dårlige modeller.

Statistiker J. Michael Steele har vært kritisk til ordtaket (se dette personlige essayet). Steeles primære argument er at «feil» bare kommer inn i spill hvis modellen ikke svarer riktig på spørsmålet som den hevder å svare på (f. eks., at en bygning på et kart er mislabeled, ikke at bygningen er representert av et lite torg). Steele går videre til staten:

flertallet av publiserte statistiske metoder sult for en ærlig eksempel.

Steele hevder at statistiske modeller ofte ikke er opp til et tilstrekkelig treningsmål, og mange modeller utviklet av statistikere er ikke tilstrekkelige for deres tiltenkt bruk.

I artikkelen Statistikk Som Vitenskap, Ikke Kunst: The Way To Survive in Data Science, Mark van Der Laan (Statistikk VED Uc Berkeley) attributter boksen sitat som en medvirkende årsak til dårlige statistiske modeller og avviser det som «fullstendig tull.»Han fortsetter å skrive:

grunnlaget for statistikk (…) kunne ikke vært å vilkårlig velge en» praktisk » statistisk modell. Men det er nettopp det de fleste statistikere gjør, stolt med henvisning til sitatet, «Alle modeller er feil, men noen er nyttige.»På grunn av dette er modeller som er så urealistiske at de er indeksert av en endelig dimensjonal parameter fortsatt status quo, selv om alle er enige om at de er kjent for å være falske.

Som en løsning kaller Van Der Laan statistikere til å slutte å bruke Box sitat, og gjøre en forpliktelse til å ta data, statistikk og den vitenskapelige metoden på alvor. Han oppfordrer statistikere til å bruke tid på å lære hvordan data i et gitt datasett ble generert og forplikte seg til å utvikle realistiske statistiske modeller ved hjelp av maskinlæring og data-adaptive estimeringsteknikker over mer tradisjonelle parametriske modeller.

denne artikkelen har svar Fra Statistikere Michael Lavine Og Christopher Tong, samt et svar på svarene fra den opprinnelige forfatteren. De to motbevise statistikerne peker på eksempler der modeller er kjent for å være feil, men ofte er ansatt fordi de er nyttige og passer for et gitt problem. Deres eksempler inkluderer de tre forskjellige lysmodellene som finnes innen optikk (geometrisk optikk, fysisk optikk og kvanteoptikk; alle tre modellene representerer lys annerledes, er «feil» på en eller annen måte, og er fortsatt ansatt i dag), og det (nesten) lineære forholdet mellom loggen av karbonfluss og jordtemperatur funnet i data samlet i Harvard Forest.

i sin tur svarer Van Der Laan på disse eksemplene og andre kritikker av sin artikkel, spesielt hans konsept om å finne en «sann» modell. Svarbrevene er definitivt verdt a lese hvis du er interessert. Dette representerer et aktivt debattområde innen statistikk og datavitenskap.

Men Noen Modeller Er Nyttige

til tross for modellens begrensninger, kan mange modeller være svært nyttige. Fordi de er forenklet, er modeller ofte nyttige for å forstå en bestemt komponent eller fasett av et system.

i sammenheng med datavitenskap kan maskinlæring og statistiske modeller være nyttige for å estimere (forutsi) ukjente verdier. I mange sammenhenger, hvis modellens forutsetninger holder seg, kan et usikkert estimat gitt av en sterk statistisk modell fortsatt være svært nyttig for å ta beslutninger.

Den andre, mindre siterte halvparten Av George Box visdom er dette:

«det praktiske spørsmålet er hvor feil gjør (modeller) må være å ikke være nyttig.»- George Box

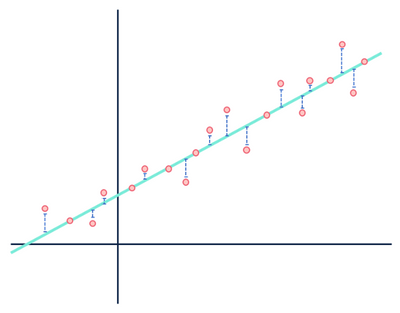
La oss ta en titt på vårt lineære regresjon eksempel:

For det meste brukte jeg for mye tid på dette bildet for å bruke det bare en gang.

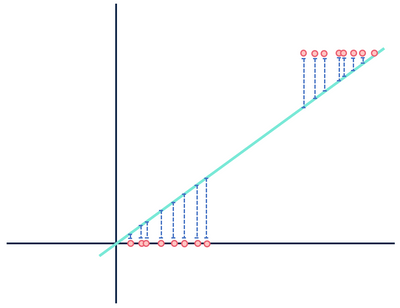
La Oss nå se på en annen teoretisk lineær regresjonsmodell som passer til et annet datasett.

Ikke Bry deg om avstandene … vent dette kan ikke være riktig.

begge tallene viser feil, men ett datasett viser et klart lineært forhold mens det andre er logistisk. Begge modellene er «feil», men man fanger tydelig et reelt forhold mellom variabler, mens den andre ikke gjør det, noe som gjør en nyttig og en ubrukelig. Å forkaste avstandene i blått som støy er rimelig hvis dataene har et lineært forhold, men denne antagelsen faller fra hverandre når forholdet har en annen funksjonell form enn den valgte modellen.

Å Lage Gode Modeller

det faktum at modeller er feil eller begrenset i omfanget av det de representerer, kan virke åpenbart for mange som jobber med modeller, men dessverre er det mange som ikke skjønner det eller tenker mye på det. Det er derfor jeg føler det er viktig å holde Ordene Til George Box i tankene når du utvikler en modell. Det bør ikke brukes som en unnskyldning for å bygge dårlige modeller.

For videre lesing Har Steele noen gode klassenotater: Gir Modellen Mening? Gir Modellen Mening? Del II: Utnyttelse Av Tilstrekkelighet. En annen stor ressurs er papiret ‘Alle modeller er feil…’: en introduksjon til modellusikkerhet fra et modellvalgsverksted holdt i 2011 I Groningen.

En annen interessant lesning Er Når Alle Modeller Er Feil Fra Problemer I Vitenskap og Teknologi, som kaller Box ord som en oppfordring til strengere åpenhet i vitenskapelige og statistiske modeller.

det viktigste å ta bort fra alt dette er å sørge for at du forstår hvilke aspekter av dataene dine som er fanget av modellen din, og hvilke aspekter som ikke er. Det er viktig å sjekke dine forutsetninger og utgangspunkt. Som statistiker eller datavitenskapsmann er det ditt ansvar å produsere strenge modeller, samt kjenne sine begrensninger. Rapporter alltid usikkerheten din, samt omfanget av modellen din. Med det i tankene, vil du være i stand til å lage modeller som, mens muligens feil, kan sikkert være nyttig.

Original. Reposted med tillatelse.

Bio: En geograf ved trening og en data geek på hjertet, Sydney mener sterkt at data og kunnskap er mest verdifulle når de kan være tydelig kommunisert og forstått. I sin nåværende rolle Som Senior Data Science Content Engineer, får hun tilbringe dagene med å gjøre det hun elsker best; forvandle teknisk kunnskap og forskning til engasjerende, kreativt og morsomt innhold for Alteryx-Samfunnet.

Relatert:

• De 3 Største Feilene ved Å Lære Datavitenskap
• 3 Store Problemer Med Store Data Og Hvordan Du Løser Dem
• Velge Mellom Modellkandidater