Rask G-Kode Arc Tutorial: Gjør G02 & G03 Lett, Unngå Feil
Sirkulær Interpolering Er Bevegelse Langs En Sirkelbue
Etter å ha nettopp ferdig med å diskutere lineær interpolering, eller bevegelse i en rett linje, kommer vi neste til sirkulær interpolering, som er bevegelse langs en sirkelbue. Annet enn den ganske eksotiske evnen til å følge en» NURBS » – bane, støtter de fleste g-kodekontrollere bare to typer bevegelser: lineær og sirkulær. Sirkulær interpolering er ganske mye mer krevende på maskinen din, da to akser må koordineres nøyaktig. Tegning av en komplett sirkel innebærer ikke bare koordinert bevegelse, men reversering av retning ved hvert av de 4 kvadrantpunktene. Disse vil være punktene som tilsvarer 0, 90, 180 og 270 grader. Hvis maskinen har noen tilbakeslag i det hele tatt, vil det være åpenbart ved disse reverseringene fordi det vil være en feil i kuttet der.
Sirkulær Bevegelse Er En Modus Initiert Via G02 Og G03
som lineær bevegelse (initiert Av G00 Og G01), sirkulær bevegelse er en modus initiert Via G02 Eller G03. G02 etablerer en modus for sirkelbuer med klokken. G03 etablerer en modus for mot klokka sirkulære buer.

Definere En Bue For CNC-Kontrolleren
når Enten G02-eller G03-modusen er etablert, defineres buer I G-Kode ved å identifisere deres 2 endepunkter og senteret som må være equi-fjernt fra hvert endepunkt, eller det vil oppstå en alarm. Endepunktene er enkle. Gjeldende kontrollpunkt, eller plassering når blokken er begynt etablerer ett endepunkt. DEN andre kan etableres VED XYZ koordinater. Senteret er litt mer komplekst.
Definere Senteret Via Ijk Relative Offsets
senteret identifiseres oftest ved å bruke I, J eller K for å etablere relative offsets fra startpunktet til buen til senteret. Her er en typisk med urviseren bue:

Definere en bues senter med IJK…
denne buen starter VED X0Y2 og avsluttes VED X2Y0. Det er sentrum er PÅ X0Y0. Vi kunne spesifisere det i g-kode som dette:
G02 (Sett opp med klokken bue modus)
X2Y0 I0J-2.0
I og J angir relative koordinater fra startpunktet til midten. Med andre ord, hvis vi legger til i-verdien til startpunktets X, Og j-verdien Til startpunktets Y, får Vi X Og Y for senteret.
Definere Senteret Via Radiusen Ved Hjelp Av»R»
Vi kan også definere senteret bare ved å angi radiusen til sirkelen. I dette tilfellet har sirkelen vår en radius på 2, så g-koden kan være ganske enkelt:
G02
X2Y0 R2
Mange av dere vil bestemme her og nå at Siden R er lettere å forstå og kortere å skrive, skal du bare bruke R og glemme IJK. MEN CNC-lærerne i verden vil foreslå at du bør foretrekke IJK. Deres argument er at når du bruker IJK, får du en dobbeltsjekk at buen din er riktig.
Hvorfor?
fordi kontrolleren får å beregne et faktisk sett med koordinater for senteret via ijk. Når det har senterets koordinater, kan det kontrollere at det er equa-fjernt fra begge endepunktene. Kontrollen av hver av disse to avstandene er dobbeltsjekken. I tilfelle av» R » – formatet har kontrolleren ingen slik dobbeltsjekk. Det må velge et senter som garanterer lik avstand.
Personlig vet Jeg Ikke om JEG er enig MED CNC-instruktørene om at dette gir ekstra kontroll eller ikke. Jeg sier gå med hvilken tilnærming som gir mening for din spesielle situasjon, men du bør definitivt være kjent og komfortabel med begge. Du må være komfortabel med relative koordinater uansett, da de er darned hendig. Kan like godt bli komfortabel nå.
Det er litt som å bli fortalt at du bare skal bruke 4-kjeve chucken på en dreiebenk når du først starter, slik at du blir veldig komfortabel å ringe den inn. Det er en god ferdighet å være god på som maskinist!
Variasjoner I Arc Syntaks For Forskjellige G-Kode Dialekter Og Moduser
Når IJK Ikke Er Inkrementell og Hva Med Å Ha Både Ijk og R? Plus, Andre Modale Shenanigans Og Buevariasjoner
Dette er et annet av de stedene hvor mange uklare ting skjer, og du trenger å vite hva kontrolleren din vil gjøre uten å anta noe. Generelt skal regelen være at hvis du har både ijk og R i samme blokk, Har R forrang og Ijk ignoreres. Men det er kontroller som ikke fungerer akkurat slik, så vær sikker på at du vet hva som skjer.
G-Wizard Editor lar deg angi flere parametere i Innlegget som bestemmer hvordan buer fungerer. Her er et skjermbilde av oppsettalternativene:
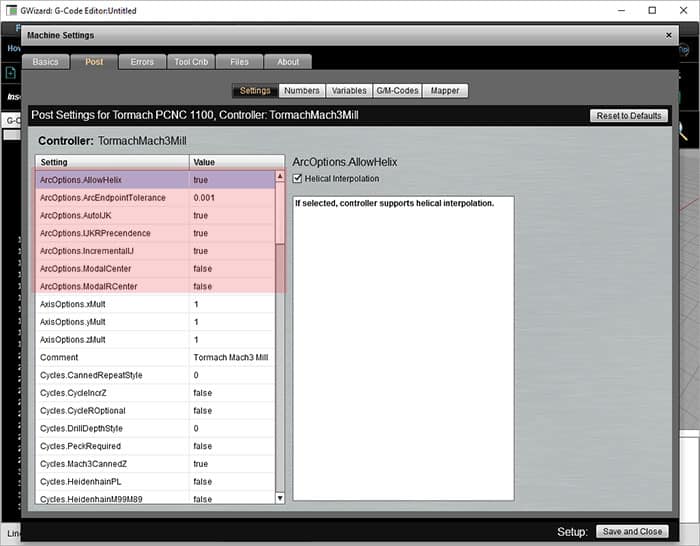
Arc Alternativer For G-Kode Simulering
La oss gå over disse alternativene:
– Inkrementell vs Absolutt Ijk:Vi har diskutert IJK som tilbyr koordinater i forhold til utgangspunktet for senteret. Legg I Til X, J Til Y, Og K Til Z på startpunktet og du får sentrum. Mange kontroller har også muligheten FOR IJK å være de absolutte koordinatene til senteret.
– Modale Ijk-Sentre: Når Ijk er absolutte senterkoordinater, vil noen kontrollere huske det siste senteret definert, derfor er ijk modal i så fall. Når du bruker en kontrolloppsett som dette, kan du bare fortsette å utstede XYZ-kommandoer for buer uten å måtte definere et nytt senter hver gang. Det er ikke klart at du vil spare mye skjønt-hvor ofte vil du gjøre en haug med buer med samme senter–
– Modal R Centers: En annen variant av modal center ideen er å tillate radius definert av » R » å være modal. Uansett hva Den siste r brukte var, husker kontrolleren og bruker den verdien igjen hvis Ingen R er gitt. Dette virker mer nyttig enn modal IJK. For eksempel kan en lomme ha buer for hjørnene som alle har samme radius.
– Gi R Forrang: som nevnt vil de fleste kontrollere bruke » R «når både» R «og» IJK » er gitt i samme blokk. Men dette alternativet lar deg endre den forrang TIL IJK hvis kontrolleren fungerer på den måten i stedet.
– Spiralformet Interp.: Dette alternativet styrer om kontrolleren tillater spiralformet interpolering.
Det Vanligste Problemet Med Å Konfigurere EN CAM-Post Eller CNC-Simulator: Absolutt vs Relativ IJK
Vi har alle hatt opplevelsen av å se på en backplot (eller verre, se det i selve verktøybevegelsen som er ganske skummelt) og se de gigantiske nesten komplette kretsene og ingen tegn på de kjente delbevegelsene vi forventet å se. Her er et typisk eksempel:
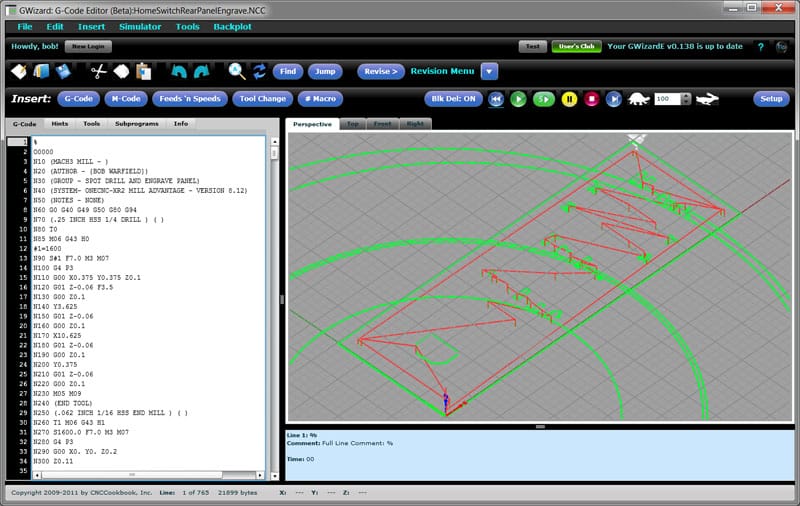
Graver fil med dårlige Innleggsinnstillinger For Buer…
hvis du ser den slags ting, er den første tingen å sjekke absolutt versus relativ ijk for buer. Innstillingen må samsvare mellom HVA KAMERAET produserer og hva kontrolleren eller simulatoren forventer.
Prøv Vår G-Kode Simulator Og Editor, Gratis
Fraksjoner Av En Sirkel, Kvadranter Og Kontrollere
det første med en bue er at det ikke er mulig å spesifisere mer enn en 360 graders bue. Det er noen unntak fra dette på noen kontroller for Spiralformet Interpolering (se nedenfor), bare fordi det kan være nyttig for helixer. Når en full sirkel er ønsket, sett start – og sluttpunktene lik hverandre:
G01 X3. 25 Y2.0
G02 X3.25 Y2.0 i-1.25 J0
Interessant, kan du ikke angi en full sirkel med «R» notasjon. Dette skyldes at det er et uendelig antall sirkler som starter og slutter på samme punkt av en bestemt radius, så kontrolleren har ingen anelse om hva den riktige sirkelen kan være.
det er mer morsom virksomhet fortsatt med » R » og større buer. For eksempel kan en bue fortsatt være av en bestemt radius og med urviseren (eller mot urviseren), men senteret er tvetydig hvis du reiser mer enn 90 grader. For eksempel:
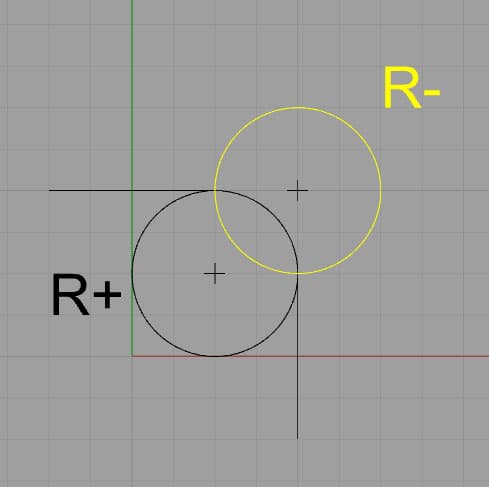
hvis R er negativ, tar den lengre banen (i gul). Positive får kortere vei.
gitt de to valgene som vises, velger kontrolleren banen basert på radiusens tegn. Negative krefter lengre bue, positive kortere. Det negative tegnet tvinger kontrolleren til å søke en levedyktig bue på mer enn 180 grader.
Noen kontrollere er touchier fortsatt og vil ikke programmere en bue som krysser en kvadrantlinje. Derfor er den største vinkelen en bue kan følge 90 grader, og den vinkelen må ikke krysse 0, 90, 180 eller 270 grader. For vinkler på 90 grader som krysser en kvadrantlinje, må de brytes i to stykker, med sammenføyningen mellom stykkene som ligger rett på kvadrantlinjen.
Fulle Sirkler Uten XYZ
Fulle sirkler oppstår når start-og endepunktene er identiske og senteret er spesifisert via IJK (husk, r fører til et uendelig antall sirkler). Gitt at du vil at start-og sluttpunktet skal være det samme, trenger du kanskje ikke å bry deg med å spesifisere sluttpunktet MED XYZ. Noen kontroller kan kreve det, men de fleste gjør det ikke. Her er et enkelt g-kodeprogram som produserer 3 sirkler på denne måten:
N45 G0 X-2. Y. 75
N46 G1 Z-.5 F10.
N47 Y. 5 F30. S2000
N48 G2 J-1,1
N49 G1 Y. 75
N50 Z. 2
N51 G0 X. 75 Y-3,4
N52 G1 Z-.5 F10.
N53 X. 5 F30.
N54 G2 I-1,1
N55 X. 75
N56 Z. 2
N57 G0 X-4,75 Y-3,4
N58 G1 Z -.5 F10.
N59 X-4,5 F30.
N60 G2 I1.1
N61 G1 X-4,75
N62 Z. 2
Og her er hva bakplottet ser ut:
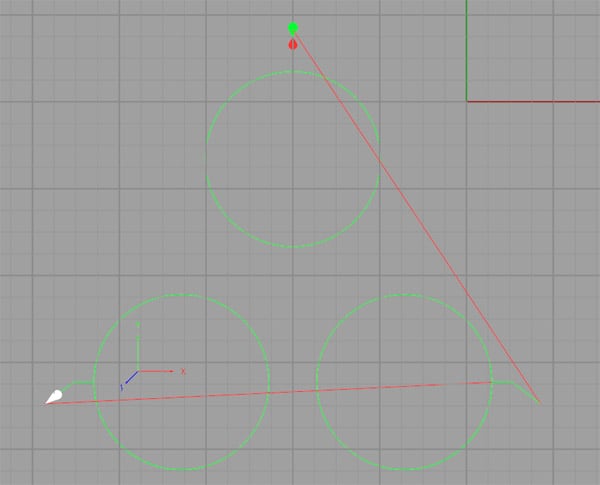
Tips For Å Gjøre Arc Programmering Enklere: Start Med Segmenter
når jeg legger ut en verktøysti, foretrekker jeg å forlate buene til sist. I stedet for hver bue legger jeg bare et linjesegment hvis endepunkter samsvarer med bueens endepunkter. Dette gjør det enkelt å få den grove skissen av verktøystien sammen raskt, og det ser ofte ut til å gjøre det lettere å gå tilbake og konvertere linjene til buer når grunnstrukturen allerede er på plass.
Spiralformet Interpolering
en helix er en bue som kontinuerlig beveger seg i en tredje dimensjon, som en skruegjeng. Med spiralformet interpolering spesifiserer vi en slik bue Med G02 / G03 for å flytte kutteren langs en helix. Dette kan gjøres for trådfresing, interpolering av et hull eller en rekke andre formål. Her er en backplot fra et 1 / 4″ NPT trådmølle program:
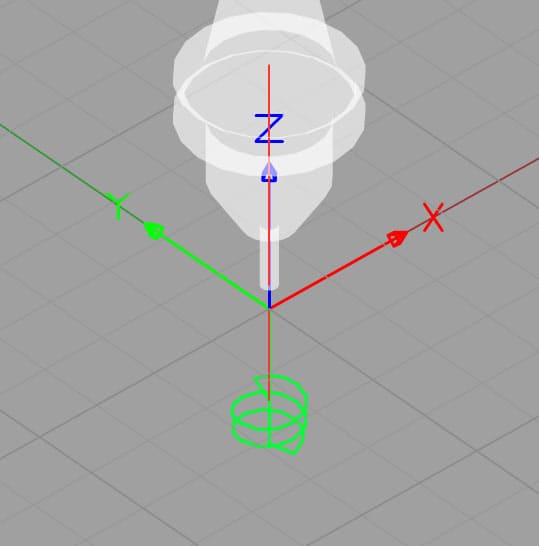
Helix for trådfresing…
her er et eksempel på koden fra trådfreseprogrammet:
G01 G91 Z-0,6533 F100.
G01 G42 D08 X0. 0235 Y-0,0939 F10.
G03 X0.0939 Y0.0939 Z0.0179 R0. 0939
G03 X-0,1179 Y0. 1179 Z0.0179 R0. 1179
G03 X-0,1185 Y-0,1185 Z0.0179 R0.1185
G03 X0.1191 Y-0,1191 Z0.0179 R0.1191 F16.
G03 X0.1196 Y0.1196 Z0.0179 R0. 1196
G03 X-0,1202 Y0.1202 Z0.0179 R0.1202 F26.
G03 X-0,1207 Y-0,1207 Z0.0179 R0.1207
G03 X0.1213 Y-0,1213 Z0.0179 R0.1213
G03 X0.1218 Y0.1218 Z0.0179 R0.1218
G03 X-0,0975 Y0.0975 Z0.0179 R0.0975
Dette er» R » (radius) format for buene, og merk at Det Er En Z-koordinat for å angi en dybdeendring for sluttpunktet til hver bue. Denne koden bruker relativ bevegelse (G91), slik at Hver «Z0.0179″ beveger kutteren 0.0179» dypere.
G-Wizard Editor gir noen virkelig nyttig informasjon for å hjelpe til med å forstå spiralformet interpolering. Her Er Hinten fra den tredje linjen (første bue flytte):

merk tråden banen her er beregnet som 0.1″
GWE vil måle og fortelle deg helix banen, som i dette tilfellet er 0.100″. Det kan være nyttig for å identifisere hva slags tråd som blir malt. Vi kan også se at denne spesielle buen går fra 270 grader til en scosh mer enn null (0,1 grader).
vi vil revidere trådfresing i mye mer detalj i et senere kapittel viet helt til emnet. For nå ville vi bare at du skulle være kjent med ideen om at du kan lage helixer så vel som flate todimensjonale buer.
Making Toolpaths Maskinen Din Vil Bli Lykkeligere Med
Når kutteren endrer retning, legger den til en viss mengde stress. Kutteren vil bite inn i materialet enten mer eller mindre enn det hadde vært, avhengig av om retningene endres mot arbeidsstykket (eller uklippet materiale) eller bort fra det. Maskinen din vil bli mye lykkeligere hvis du programmerer en bue i stedet for en brå rettlinjeskifte. Selv en bue med en svært liten radius vil tillate kontrolleren å unngå å endre retning umiddelbart, noe som kan gi et merke i finishen i beste fall og forårsake chatter eller andre problemer i verste fall. For små endringer i retning, kan det ikke være verdt det. Men jo mer brå endringen, med 90 grader er veldig brå, desto større er sannsynligheten for at du bør bruke en bue for å lette gjennom svingen.
Buer er også en nyttig måte å gå inn i kuttet, i stedet for å ha kutteren lekter rett inn. For informasjon om å skrive inn kuttet med en bue, se toolpath siden Fra Fresing Feeds Og Hastigheter Kurs.
Øvelser
1. Grav UT CNC-kontrollerhåndboken og gå gjennom arc-innstillingene for å sette OPP GWE for å matche kontrollens måte å operere på.
2. Gjør noen etch-a-skisse eksperimentering med GWE. Lag noen verktøystier som inkluderer buer til du er komfortabel med å lage dem.
Neste Artikkel: Kjører GWE G-Code Simulator
Prøv Gratis Prøveversjon Av G-Wizard G-Code Editor…