Skjult Markov-Modell: Enkel Definisjon Og Oversikt

Statistikk Definisjoner >

Hidden Markov-Modellen (HMM) er en relativt enkel måte å modellere sekvensielle data på. En skjult Markov-modell innebærer At Markov-Modellen som ligger til grunn for dataene, er skjult eller ukjent for deg. Nærmere bestemt vet du bare observasjonsdata og ikke informasjon om statene. Med andre ord er det en bestemt type modell som produserer dataene (En Markov-Modell), men du vet ikke hvilke prosesser som produserer den. Du bruker i utgangspunktet din kunnskap Om Markov-Modeller for å gjøre en utdannet gjetning om modellens struktur.

Hva Er En Markov-Modell?

for å avdekke Den Skjulte Markov-Modellen må du først forstå hva En Markov-Modell er i utgangspunktet. Her skal jeg lage et enkelt eksempel ved hjelp av to elementer som er veldig kjent i sannsynlighet: terninger og poser med fargede baller.

modellkomponentene, som du vil bruke til å lage den tilfeldige modellen, er:

• en seks-sidig rød dør.
• en ti-sidig svart dør.
• en rød pose med ti baller. Ni baller er røde, en er svart.
• en svart pose med tjue baller. En ball er rød, nitten er svart.

«Svart» Og » Rød » er de to statene i denne modellen(med andre ord, du kan være svart, eller du kan være rød).
opprett nå modellen Ved å følge disse trinnene:

1. UTSLIPPSTRINN: Rull en dør. Legg merke til nummeret som kommer opp. Dette er emisjonen. I grafikken ovenfor valgte jeg en rød dør for å starte (vilkårlig — jeg kunne ha valgt svart) og rullet 2.
2. OVERGANGSTRINN: Velg Tilfeldig en ball Fra posen med fargen som passer til terningen du rullet i trinn 1. Jeg rullet en rød dør, så jeg skal velge en ball fra den røde posen. Jeg trakk ut en svart ball, så jeg skal gå over til den svarte dør for neste utslipp.

du kan deretter gjenta disse trinnene til et visst antall utslipp. Hvis du for eksempel gjentar denne sekvensen av trinn 10 ganger, kan du få settet {2,3,6,1,1,4,5,3,4,1}. Prosessen med overgang fra en stat til den neste kalles En Markov-prosess.

Overgang fra rød til svart eller svart til rød har forskjellige sannsynligheter, da det er forskjellige antall svarte og røde baller i posene. Følgende diagram viser sannsynlighetene for denne modellen, som har to tilstander (svart og rødt):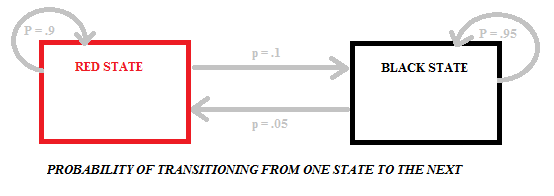

Skjult Markov Modellnotasjon

λ = (A,B,hryvnja), er kortnotasjon for EN HMM. Annen notasjon brukes I Skjulte Markov-Modeller:

• a = tilstandsovergangssannsynligheter (aij)
• B = observasjonssannsynlighetsmatrise (bj(k))
• N = antall tilstander i modellen {1,2…N} eller staten ved tidspunktet t →st
• M = antall distinkte observasjonssymboler per stat
• Q = {q0, q1, . . . , qN−1} = distinkte tilstander Av Markov-prosessen
• T = lengden av observasjonssekvensen
• V = {0, 1, . . . , M − 1} = sett med mulige observasjoner
• O = (O0, O1, . . . , OT -1) = observasjonssekvens
• π = opprinnelig tilstandsfordeling (ni)
• s = statlig eller tilstandssekvens (s1, s2… sn)
• xk = skjult tilstand
• zk = observasjon.

Tre Grunnleggende Problemer

Tre grunnleggende problemer kan løses Med Skjulte Markov-Modeller:

1. Gitt Den Skjulte Markov-Modellenλ = (A, B, π) Og en rekke observasjoner O, finn sannsynligheten For en observasjon P (O / λ). Dette kalles Noen Ganger Evalueringsproblemet.
2. Gitt Den Skjulte Markov-Modellenλ = (A, B, π) Og en observasjonssekvens O, finn den mest sannsynlige tilstandssekvensen (s1, s2 … sn). Dette kalles Noen Ganger Et Dekodingsproblem.
3. Finn en observasjonssekvens (O1, O2 … På Og Skjult Markov Modell λ = (A, B, π) som maksimerer sannsynligheten For O. Dette kalles Noen Ganger Et Læringsproblem eller Optimaliseringsproblem.

Rabiner, L. R. «en tutorial på skjulte Markov modeller og utvalgte programmer i talegjenkjenning», Proceedings of THE IEEE, vol.77, s.257-286, Feb. 1989.
Stempel, M. (2013). En Avslørende Introduksjon Til Skjulte Markov-Modeller. Hentet 8/6/2013 fra: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

Trenger du hjelp med lekser eller testspørsmål? Med Chegg Study kan du få trinnvise løsninger på dine spørsmål fra en ekspert på feltet. Din første 30 minutter med En Chegg veileder er gratis!