Solsystemet: Jorden Og Månen
planetene er titalls og hundrevis av millioner kilometer unna oss. For å unngå bruk av så store tall, er Den Astronomiske Enheten (AU) vedtatt som avstandsenhet, det vil si gjennomsnittlig avstand mellom Jorden og Solen, 149.600.000 km.Lys tar 8 minutter og 19 sekunder for å dekke denne avstanden.
Størrelsen på Solsystemet overskrider plutos bane ved 40 AU og er definert som en hvor solens tiltrekningskraft er lik tiltrekningskraften til stjernene nærmest oss. Dimensjonene Til Solsystemet vil da være i størrelsesorden 1, 5 105 AU. Åpenbart er disse dimensjonene svært små i forhold til dimensjonene til galaksen eller det synlige Universet. Enhetene som er tatt for å måle disse enorme avstandene, er lysåret og parsec som tilsvarer 206 265 AU eller 3, 26 lysår.
planetene i Solsystemet er delt inn i to grupper: den terrestriske gruppen dannet Av Merkur, Venus, Jorden Og Mars og giant planets gruppen dannet Av Jupiter, Saturn, Uranus og Neptun.
alle planeter unntatt Venus og Merkur har satellitter, hvorav de fleste tilhører kjempeplanetene. Jorden, Jupiter, Saturn Og Neptun har de største satellittene: Månen, satellittene Til Jupiter oppdaget Av Galileo (Io, Europa, Ganymede, Callisto), satellitt Titan Av Saturn Og Triton Av Neptun.
Asteroider okkuperer et stort ringformet område mellom banene Til Mars og Jupiter, med en gjennomsnittlig avstand på 2,75 AE FRA Solen. Den største asteroiden Er ceres som har en diameter på 1000 km.
Kometer, som har blitt katalogisert om 600, er delt inn i to grupper, kort periode (under 20 år) og lang periode (over 20 år). Det er flere hypoteser om kometenes opprinnelse, inkludert den nederlandske astronomen J. Oort.
i tillegg til kroppene nevnt i interplanetarisk rom, er det et stort antall partikler av forskjellige størrelser, hovedsakelig de med en masse tusendeler eller milliondeler av gram, som kalles meteorisk støv. Dannelsen av disse partiklene skyldes sannsynligvis kollisjonen av større legemer (asteroider) og deres suksessive fragmentering gjennom Solsystemets eksistens og utvikling.
Meteorisk støv er ansvarlig for fenomenet dyrekretsen, som observeres etter skumring eller før daggry, på grunn av spredning av lys av disse støvpartiklene. De fleste partikler fordamper når De kommer inn I jordens atmosfære (i høyder mellom 80 og 120 km), bare en liten andel når jordens overflate.
La oss nå se på noen data relatert til planeter Av Solsystemet
Første Av Solen
| himmellegeme | Radio | Masse |
|---|---|---|
| Sol | 6,96 * 108 m | 1,98 * 1030 kg |
deretter, ut Av Landet
| himmellegeme | store halvakse | Periode | Masse |
|---|---|---|---|
| Jord | 149,6·109 m | 1 år=365,26 dager | 5.98 * 1024 kg |
resten av planetene
| Planet | store halvakse (AU) | Eksentrisitet | Periode (år) | Masse |
|---|---|---|---|---|
| Merkur | 0.387 | 0.206 | 0.24 | 0.06 |
| Venus | 0.723 | 0.007 | 0.62 | 0.82 |
| Jorden | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturn | 9.539 | 0.056 | 29.46 | 95.1 |
| Uranus | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptuns | 30.058 | 0.009 | 164.8 | 17.2 |
i tabellen nedenfor er gitt som supplerende data:
- helling av planetens bane i forhold til ekliptikken (planet Av jordens bane)
- rotasjonsperioden rundt sin akse. Det har vært svært vanskelig å måle denne størrelsen for planeter Som Merkur og Venus. De gassformige skallene Til Jupiter, Saturn, Uranus og Neptun har egenskapen til differensial rotasjon, det vil si at deres rotasjonsperioder varierer i henhold til breddegrad.
- helling av rotasjonsaksen med hensyn til baneplanet. For Venus er det 177º som tilsvarer å si at hellingen til aksen er 3º, men rotasjonsretningen er omvendt. Det samme argumentet gjelder For Uranus, noe som indikerer At Rotasjonsaksen til Uranus er nesten i planet av sin bane.
| Planet | Inklinasjon i bane | rotasjonsperiode | Tetthet g/cm3 | radioekvator (km) | aksevinkel | Nei. av satellitter |
|---|---|---|---|---|---|---|
| Merkur | 7.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Venus | 3.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| Jorden | 0 | 23h.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1.8 | 24 timer.6 | 3.95 | 3 394 | 25º2 | 2 |
| Jupiter | 1.3 | 9h.9 | 1.33 | 71 398 | 3.1 | 16 |
| Saturn | 2.5 | 10t.2 | 0.69 | 60 000 | 26º4 | 17 |
| Uranus | 0º8 | 10t.8 | 1.26 | 25 400 | 98º | 5 |
| Neptun | 1.8 | 15h.8 | 1.67 | 24 750 | 29º | 2 |
Satellitter
Til Slutt gir Vi noen data om planets store satellitter. Jupiter og Saturn har mange satellitter som er mye større Enn Mars, men vi nevner bare de som er like i størrelse eller større enn Vår Måne.
| Planet | Satellitter | Tetthet g / cm3 | gjennomsnittlig Radius (km) | radiobane (103 km) | Periode (dager) |
|---|---|---|---|---|---|
| Jorden | Måne | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturn | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptun | Newt | 2 200 | 394.7 | 5.84 |
Aktiviteter
- Bestem Massen Av planeten Jupiter fra radiodataene og revolusjonsperioden for en av satellittene.
- Bestem radiusen til bane av en satellitt På Planeten Jupiter fra massen av den planeten og revolusjonsperioden for satellitten.
- Bestem intensiteten av gravitasjonsfeltet g på overflaten av planeter og noen satellitter, fra dataene av deres masse M Og deres radius R eller deres tetthet ρ og deres radius.
eksempel: bestem Massen Til Planeten Jupiter, vel vitende om at Radien til Ios bane er 421 600 km og at dens revolusjonsperiode er 1 769 dager. Fakta: konstanten G er 6,67 * 10-11 Nm2/kg2
Eksempel: Beregn radiusen til bane av satellitten Callisto å vite at revolusjonsperioden er 16.689 dager og Massen Av Planeten Jupiter er 1.901·1027 kg. Data: konstanten G er 6,67 * 10-11 Nm2 / kg2
g=G M R 2 = 4π 3 GpR
Data: konstanten G er 6.67 * 10-11 Nm2 / kg2
Månen
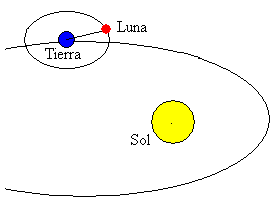
Månen er en av De største kroppene i Solsystemet. Dens bane er nesten sirkulær (eksentrisitet ε=0,05) og planet av sin bane er tilbøyelig 5º med hensyn Til planet Av Jordens bane.
gjennomsnittlig avstand mellom sentrum Av Jorden og Månen er 384.400 km.Rotasjonsperioden rundt Jorden er 27.322 dager. Endringen Av månens posisjon i forhold Til Solen gir opphav til månens faser.
Månen presenterer alltid det samme ansiktet til den terrestriske observatøren, på grunn av effekten Av tidevannskreftene Som Jorden utøver på Månen. Hvilket betyr At rotasjonsperioden for Månen rundt sin akse sammenfaller med tiden det tar å fullføre en bane rundt Jorden.
Månen Er det himmelske objektet som har mest fascinert den menneskelige arten. Det tidligere Sovjetunionen sendte først et automatisk skip som landet På Overflaten Av Månen i 1959. Den 20. juli 1969 Var Neil Armstrong ledsaget Av Edwin Aldrin de første mennene som gikk på Overflaten av Månen som En Del Av Apollo 11-oppdraget. Det siste besøket Av Amerikanske astronauter til Månen fant sted i 1972.
Månens opprinnelse virker usikker, det er flere teorier:
-
Det ble dannet Samtidig Jorden Med materialet fra en nebula
-
en himmellegeme er delt inn i to deler, noe som gir opphav Til Jorden og Månen
-
At Månen dannet andre steder og ble fanget av Jorden
-
At Jorden kolliderte med et himmellegeme av stor størrelse (omtrent På Størrelse Med Mars eller større), Og At Månen ble dannet med materialet utvist fra denne kollisjonen.
sistnevnte teori synes for øyeblikket den mest aksepterte av det vitenskapelige samfunn.
Månebane
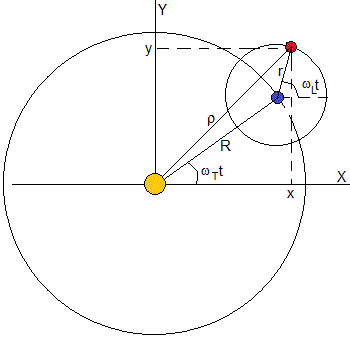
Tenk på en planet og dens satellitt. Planeten beskriver en sirkulær bane med radius R rundt sin stjerne med konstant vinkelhastighet wT=2π / PT, MED PT er perioden eller tiden som fører til en fullstendig sving. Den satellitt beskriver en sirkulær bane coplanaria med radius r med konstant angular velocity wL=2π/PL, blir PL perioden, eller tiden det tar å gjøre en fullstendig revolusjon
posisjon, satellitt-med hensyn til en referanse system hvis opprinnelse er stjernen, er
x=Rcos( ω T )+rcos( ω L t ) y=Risiko( ω T )+risiko( ω L t )
Er α=wT/wL
{ x=Rcos( α ω L t )+rcos( ω L t ) y=Risiko( α ω L t )+risiko( ω L i t t ) { x=Rcos( α 2π S L t )+rcos( 2π S L t ) y=Risiko( α 2π S L t )+risiko( 2π S L t )
vi vil Kalle τ=t/PL
x R =cos( α·2πτ )+ r-R cos( 2πτ ) og R =sin( α·2πτ )+ r-r sin( 2πτ )
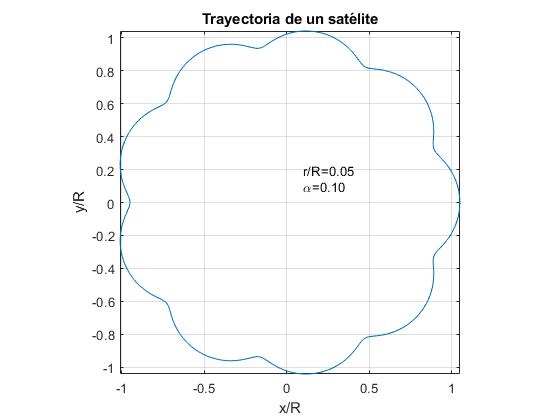
vi Representerer banen til en satellitt for α=0.1 og for tre verdier av forholdet r/R.
- r/R<α. Eksempel, r / R=0.05
- r / R=α. Eksempel, r / R=0,1
- r/r > α. Eksempel, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
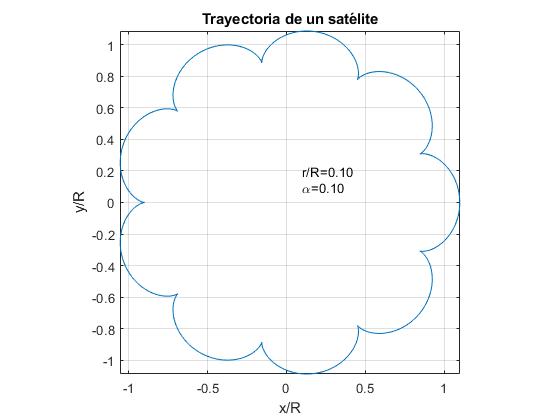
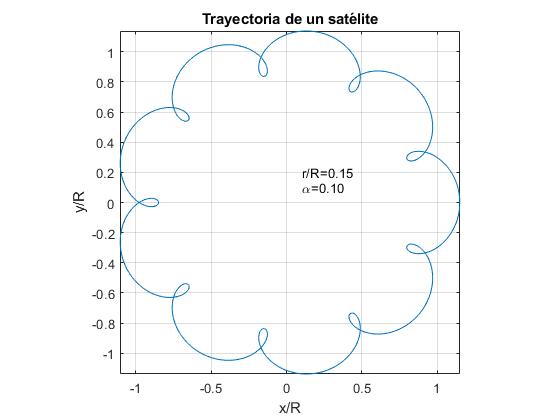
For Tilfellet Av Jorden og Månen er dataene:
- radius Av månens bane: r=384.4·106 m,periode PL = 27.32 d
- radius Av jordens bane: R = 149.6 * 109 m, periode PT = 365.26 d
α=wT/wL=PL/PT=0.0748. r / R=0.0026
månens bane vil ligne Den første figuren. I den grafiske fremstillingen av banen til Månen for disse verdier av α og r/R ikke setter pris på svingninger i den radielle avstanden mellom Solen og Månen
Akselerasjon av Månen
avstanden ρ mellom Solen og Månen, er
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )
vi Beregne den rektangulære komponenter av akselerasjon
{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L i t t ) { a x d = 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L t )
radiell komponent av akselerasjon
for å ρ = a → · ρ → ρ = a x x+ y x 2 + y 2 =− ω T 2 R 2 + ω L 2 l 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2 rr cos( ( ω L − ω T )t )
minimum og maksimum verdier er oppnådd når cos((wL-wT)t)=±1
en maks =− ω T 2 R 2 + ω L 2 l 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 l 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
Månen er den eneste satellitten i Solsystemet, hvis radiale komponent av akselerasjonen er negativ, det sies at ‘Månen faller mot Solen’,
månens faser
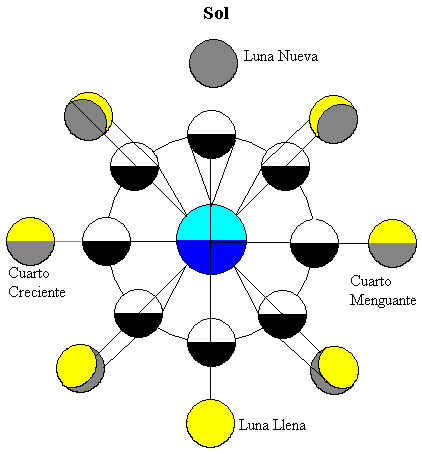
figuren viser Månen i forskjellige posisjoner i sin bane rundt Jorden. Solen er langt unna og belyser begge himmellegemene (øverst på figuren)
Halvparten av Månen er opplyst Av Solen (i hvit farge) og halvparten av Månen nærmest Jorden er synlig av terrestrisk observatør. Når Månen beveger Seg rundt Jorden, ser vi forskjellige fraksjoner av delen opplyst Av Solen (de gule områdene).
-
Når Månen er mellom Jorden og Solen, er Delen av Månen nærmest Jorden mørk, så Vi kan ikke se Månen, denne fasen kalles Nymåne.
-
Når Jorden er mellom Solen og Månen, er Den Delen Av Månen nærmest Jorden den opplyste halvdelen, denne fasen kalles Fullmåne.
-
Når Månen er i mellomposisjoner, er bare halvparten av Den nærmeste Delen Av Jorden opplyst. Derfor ser vi bare en fjerdedel Av Månen, disse to faser kalles Kvartaler, Øker eller Avtar avhengig av om den opplyste delen som er synlig Fra Jorden, har en tendens til å vokse eller redusere.
Merk: Dette interaktive programmet forsøker å forklare månens faser, men det er en trofast representasjon Av månens bane, som danner en vinkel på 5 ° med ekliptikkens plan (Jordens bane rundt Solen), eller orienteringen Av jordens akse som er omtrent 23º med det normale til ekliptikkens plan.
en rød linje er trukket over Månen, slik at leseren kan sette pris på tilfeldigheten av månens rotasjonsperiode rundt sin akse og tiden det tar å fullføre en bane rundt Jorden, Og Derfor Har Månen alltid samme ansikt til Jorden.
Formørkelser Av Månen
måneformørkelser forekommer når Månen er I full fase og Når Solen, Jorden og Månen er i en rett linje. Da Er Månen i skyggen produsert Av Jorden som vist på figuren.
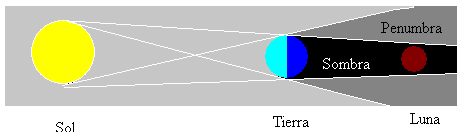
det finnes andre typer måneformørkelse, som avhenger av justeringen av de tre himmellegemene. Månen kan være i et ubelyst område (skygge) eller delvis opplyst (penumbra).
Solformørkelsen oppstår når Månen står mellom Solen og Jorden, Månen er I En Ny fase. Månen er 400 ganger mindre Enn Solen, Men Månen er 400 ganger nærmere Jorden, så den tilsynelatende størrelsen på begge legemer sett fra Jorden er nesten den samme. Månen kan dermed produsere en total solformørkelse, hvis observert i skyggesonen projisert Av Månen på Jorden.
Månedata
| Masse (kg) | 7.349·1022 |
| Radius (km) | 1737. 4 |
| Gjennomsnittlig tetthet (g/cm3) | 3.34 |
| gjennomsnittlig Avstand Til Jorden (km) | 384 000 |
| periode av bane (dager) | 27.32166 |
| Akselerasjon av tyngdekraften ved ekvator (m / s2) | 1.62 |
| Eksentrisitet av bane | 0.0549 |
| Helling av bane (grader) | 5.1454 |
-
Beregn radiusen til månens sirkulære bane rundt Jorden og vite at perioden er 27,32 dager. Beregn også månens hastighet. Data: G =6,67 * 10-11 Nm2 / kg2, jordens masse Er M = 5,98 * 1024 kg.
-
Beregn akselerasjonen av tyngdekraften g på Overflaten Av Månen.
-
Beregn kvotienten mellom solens diameter og Månens diameter. Beregn forholdet mellom gjennomsnittlig avstand Mellom Solen Og Jorden, Og Månen og Jorden. Data: Solens radius 6,96 * 108 m, midgard-Solens avstand 1,49·1011 m
-
Beregn posisjonen til massesenteret Til Jordmånesystemet, målt fra sentrum Av Jorden.
-
Beregn jordens tiltrekningskraft på Månen, sammenlign den med solens tiltrekningskraft på Månen. Dato: Solmasse, 1,98 * 1030 kg
Referanser
M. Marov. Planeter Av Solsystemet. Forlag Mir.
Lær mer Om planeter I Hvor mange planeter er det i Vårt Solsystem?. ComofuncionaQue.com
for seksjonen ‘Bane Av Månen’
David C. Johnston. Sykloidale baner i fysikk som superposisjoner av translasjonelle og rotasjonsbevegelser. Er. J. Phys.87 (10), oktober 2019, s. 808-810
Månen Svinger Alltid Mot Solen. Matte sider.