Bootstrap in R

Bootstrap is een methode om een populatie af te leiden met behulp van voorbeeldgegevens.Bradley Efron introduceerde het voor het eerst in dit papier in 1979.Bootstrap vertrouwt op sampling met vervanging van sample data. Deze techniek kan worden gebruikt om de standaardfout van een statistiek te schatten en er een betrouwbaarheidsinterval (CI) voor vast te stellen. Bootstrap is vooral handig wanneer CI geen gesloten vorm heeft, of het heeft een zeer ingewikkelde.

stel dat we een steekproef van n elementen hebben:X = {x1, x2, …, xn} en we zijn geïnteresseerd in CI voor een aantal statistieken T = t(X). Bootstrapframework is eenvoudig. We herhalen gewoon R keer het volgende schema: voor i-de herhaling, sample met vervangende n elementen uit de beschikbare sample (sommige van hen zullen meer dan eens worden geplukt). Noem dit nieuwe sample i-th bootstrap sample, Xi, en calculatedesired statistische Ti = t (Xi).

als gevolg hiervan krijgen We R-waarden van onze statistiek: T1, T2,…, TR. We noemen thembootstrap realisaties van T of een bootstrap distributie van T. gebaseerd op het, kunnen we CI berekenen voor T. er zijn verschillende manieren om dit te doen. Percentielen nemen lijkt de makkelijkste.

Bootstrap in actie

laten we (nogmaals) de bekende iris dataset gebruiken. Kijk eens naar een eerste paar rijen:

stel dat we CIs willen vinden voor mediaan Sepal.Length, mediaanSepal.Width EN Spearman ‘ s rank correlatiecoëfficiënt tussen deze twee. We gebruiken R ‘ s boot pakket en een functie genaamd… boot. Gebruik zijn kracht die we hebben om een functie te creëren die onze statistieken berekent (s) uit resampled data. Het moet ten minste twee argumenten hebben: een dataset en een vector met indices elementen uit een dataset die zijn gekozen om een bootstrap-sample te maken.

als we CIs voor meer dan één statistiek tegelijk willen berekenen, moet onze functie ze als een enkele vector retourneren.

voor ons voorbeeld kan het er zo uitzien:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo kiest gewenste elementen (welke getallen zijn opgeslagen in indices)uit data en berekent de correlatiecoëfficiënt van de eerste twee kolommen (method='s' wordt gebruikt om de rangcoëfficiënt van Spearman te kiezen,method='p' zal resulteren met de coëfficiënt van Pearson) en hun medianen.

we kunnen ook enkele extra argumenten toevoegen, bijvoorbeeld. laat de gebruiker het type odcorrelatiecoëfficiënt kiezen:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

om deze tutorial meer algemeen te maken, gebruik ik de laatste versie vanfoo.

nu kunnen we de functie boot gebruiken. We moeten het voorzien van een naam oddataset, functie die we zojuist hebben gemaakt, aantal herhalingen (R) en eventuele extra argumenten van onze functie (zoals cor.type). Gebruik set.seed voor de reproduceerbaarheid van dit voorbeeld.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot functie geeft een object van de aangeroepen klasse terug… (ja, je hebt gelijk!)boot. Het heeft twee interessante elementen. $t bevat R-waarden van onze statistieken gegenereerd door de bootstrap-procedure (bootstrap-realisaties ofT):

$t0 bevat waarden van onze statistiek (s) in originele, volledige dataset:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

boot object afdrukken op de console geeft meer informatie:

original is gelijk aan $t0. bias is een verschil tussen het gemiddelde van Bootstrap-realisaties (die van $t), een bootstrap estimateof T genoemd, en de waarde in de oorspronkelijke dataset (die van $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error is een standaardfout van bootstrap schatting, die gelijk is aanstandaarddeviatie van bootstrap realisaties.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

verschillende types bootstrap CIs

voordat we beginnen met CI, is het altijd de moeite waard om eens te kijken naar de verdeling van bootstrap realisaties. We kunnen de functie plot gebruiken, waarbijindex aangeeft op welke van de statistieken berekend in foo we willen kijken. Hier is index=1 een Spearman ‘ s correlatiecoëfficiënt tussen EPALE lengte en breedte, index=2 is een mediane od sepal lengte enindex=3is een mediane od sepal breedte.

plot(myBootstrap, index=1)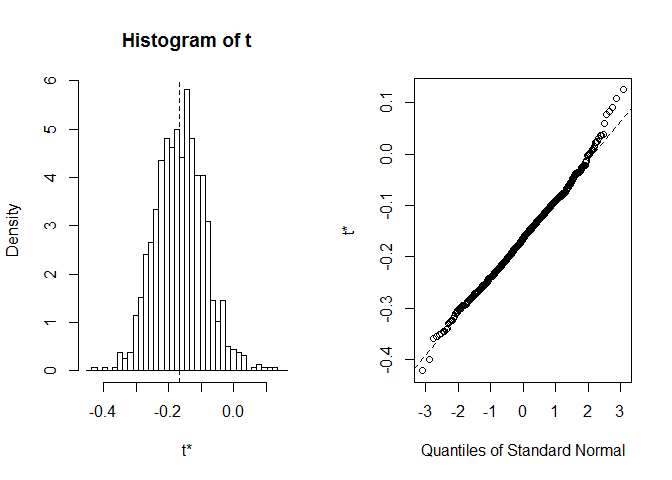

verdeling van bootstrap correlatiecoëfficiënten lijkt quitenormal-achtige. Laten we er CI voor vinden. We kunnen boot.cigebruiken. Het is standaard 95 procent CIs, maar het kan worden gewijzigd met de conf parameter.

boot.ci biedt 5 soorten bootstrap CIs. Een van hen, studentizedinterval, is uniek. Het moet een schatting van bootstrap variantie. We hebben het niet opgegeven, dus R geeft een waarschuwing af:bootstrap variances needed for studentized intervals. Variantieschattingen kunnen worden verkregen met tweede niveau bootstrap of (gemakkelijker) met Jackknife techniek. Dit valt op de een of andere manier buiten het bereik van deze tutorial,dus laten we ons richten op de resterende vier soorten bootstrap CIs.

als we ze niet allemaal willen zien, kunnen we relevante degenen kiezen in typeargument. Mogelijke waarden zijn norm, basic, stud, perc, bca of een vector van deze.

de functie boot.ci maakt object van klasse… (ja, je hebt het geraden!)bootci. De elementen ervan worden net zo genoemd als de typen CI die gebruikt worden in het typeargument. $norm is een 3-elementen vector die confidence leveland CI grenzen bevat.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc en $bca zijn 5-elementvectoren die ook percentielen bevatten die worden gebruikt om CI te berekenen (we komen hier later op terug):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

een beetje notatie (Sorry!)

om een idee te krijgen van wat verschillende typen CI zijn, moeten we enige notatie invoeren. Dus, laat:

• t⋆ worden de bootstrap schatting (gemiddelde van bootstraprealizations),
• t0 een waarde van onze statistiek in de oorspronkelijke dataset,
• se⋆ een standaard fout van de bootstrap schatting,
• b een afwijking van de bootstrap estimateb = t⋆ − t0
• α een mate van zelfvertrouwen meestal α = 0.95,
• za een $1-\frac \alpha 2$-quantile van standardnormal distributie,
• θα een α-percentiel van de verdeling van de bootstraprealizations.

percentiel BI

met bovenstaande notatie is percentiel BI:

(θ (1-α) / 2, θ1 − (1-α)/2)

dus dit neemt alleen relevante percentielen. Niets meer.

normale CI

een typische Wald CI zou zijn:

t0 ± za ⋅ se⋆

maar in bootstrap geval, moeten we het corrigeren voor vooringenomenheid. Zo wordt het:

$$ t_0-b \ pm z_ \ alpha \ cdot se^ \ star \ \ 2t_0-t^\star \pm z_\alpha \cdot se^\star$$

Basic CI

percentiel CI wordt over het algemeen niet aanbevolen omdat het slecht presteert wanneer het gaat om weird-tailed distributies. Basic CI (ook wel dpivotal of empirische CI genoemd) is hiervoor veel robuuster. De reden hiervoor is om verschillen te berekenen tussen elke bootstrap replicatie en t0 en percentielen van hun distributie te gebruiken. Volledige details zijn bijvoorbeeld te vinden in L. Wasserman ‘ s All ofStatistics

definitieve formule voor basis-CI is:

(2t0-θ1 − (1-α) / 2, 2t0-θ (1-α))/2)

BCA CI

BCa komt van bias-gecorrigeerd, versneld. De formulafor het is niet erg ingewikkeld maar enigszins onintuã tief, dus Ik zal het overslaan.Zie artikel van Thomas J. DiCiccio en BradleyEfron als je geïnteresseerd bent in details.

versnelling genoemd in de naam van de methode vereist het gebruik van specificpercentielen van bootstrap realisaties. Soms kan het gebeuren dat dit extreme percentielen zouden zijn, mogelijk uitschieters.BCa kan in dergelijke gevallen onstabiel zijn.

laten we eens kijken naar BCa CI voor de mediaan van de bloemblaadbreedte. In de oorspronkelijke dataset is deze mediaan gelijk aan precies 3.

we krijgen BCA CI (2,9, 2,9). Dat is vreemd, maar gelukkig waarschuwde Rons dat extreme order statistics used as endpoints. Laten we eens kijken wat hier precies gebeurd is.:

plot(myBootstrap, index=3)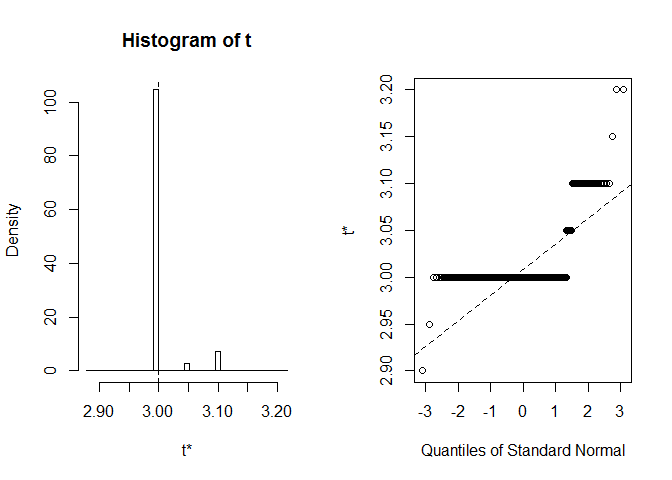

distributie van bootstrap realisaties is ongebruikelijk. Een overgrote meerderheid van hen (meer dan 90%) zijn 3s.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

replicatie van resultaten

soms moeten bootstrap-replicaties opnieuw worden gemaakt. Als we Rhiervoor kunnen gebruiken, is dit geen probleem. set.seed functie lost het probleem op.Bootstrap-replicaties opnieuw maken in andere software zou veel ingewikkelder zijn. Bovendien kan herberekening in R voor grote R ook geen optie zijn (bijvoorbeeld wegens tijdgebrek).

we kunnen dit probleem oplossen door indices op te slaan van elementen van de originaldataset, die elk bootstrap-Monster vormden. Dit is wat boot.arrayfunctie (met indices=T argument) doet.

tableOfIndices<-boot.array(myBootstrap, indices=T)

elke rij is één bootstrap-voorbeeld. Bijvoorbeeld., ons eerste voorbeeld bevat de volgende elementen:

instelling indices=F (een standaard), krijgen we een antwoord op de vraag “hoe vaak elk element van de originele dataset verscheen in elke bootstrapsample?”. Bijvoorbeeld, in de eerste steekproef: het 1ste element van de dataset verscheen op het moment dat het 2de element helemaal niet verscheen, 3de element verscheen eenmaal, 4thtwice en ga zo maar door.

een tabel als deze stelt ons in staat om bootstrap-realisatie buiten Ropnieuw te maken.Of in R zelf als we set.seed niet willen gebruiken en alle berekeningen opnieuw uitvoeren.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

laten we controleren of de resultaten hetzelfde zijn:

Ja, dat zijn ze!

als u meer wilt weten over Machine Learning in R, volg dan de Machine Learning Toolbox cursus van DataCamp.