Een Cirkel is gelijkmatig verdeeld in zes gelijke driehoeken
Hi Marilynn,
ten Eerste, ik zal je vertellen mijn aannames over hoe je foto eruit ziet:
- Elke driehoek is een hoek (hoek) in het midden van de cirkel
- Elke driehoek heeft hoeken op de omtrek van de cirkel (dus twee kanten van elke driehoek is een straal)
- De driehoeken delen zijden (er zijn geen gaapt tussen driehoeken)
Het algemene beeld lijkt op een bloem – elke driehoek is een bloemblaadje.

het onbekende gebied is wat overblijft rond de buitenkant van de cirkel, tussen de omtrek en de buitenkant van elke driehoek. Dit onbekende gebied is verdeeld in zes congruente secties (gelijk in elke manier – zoals de driehoeken zijn “gelijk” in elke manier – inclusief oppervlakte, lengte van de zijde en lengte van de boog). Het is niet duidelijk of je bedoelt dat de oppervlakte van een boog Pi is (eigenlijk niet split Pie, hoewel pronouced hetzelfde), of alle zes secties samen Pi is. In wat volgt, zal ik aannemen dat een van de buitenste secties een oppervlakte van Pi heeft, zodat de oppervlakte van alle zes secties samen 6 keer Pi is. We moeten de straal van de cirkel vinden, noem het r.
Ik zal ook P gebruiken om Pi (of CA. 3.14). Er is veel informatie die we kunnen garneren uit de driehoeken.:
- de hoeken in het midden zijn allemaal 60 graden. Dit komt omdat de zes hoeken in het centrum allemaal gelijk zijn, en een cirkel heeft 360 graden. Zo doen 360 edelen door 6.
- elke driehoek is gelijkbenig. Dit komt omdat twee zijden gelijk zijn (de zijden die een straal hebben).
- elke driehoek is in feite gelijkzijdig. Omdat het iscoceles, de twee buitenste hoeken zijn ook gelijk. Maar er is 180 graden in een driehoek, 60 zijn al gebruikt in de middenhoek, waardoor 180-60=120 graden voor de buitenhoeken. Maar 120 gedeeld door 2 is 60 graden, dus alle drie de hoeken zijn gelijk, dus het zijn isoscles.
- elke zijde in elke driehoek heeft Lengte r. Dit is omdat we 6 congruente (“gelijk” in alle opzichten) gelijkzijdige driehoeken hebben, en omdat twee zijden van elke driehoek een straal is.
vanuit de meetkunde van de driehoeken moeten we wat algebra doen. Omdat we een gebied kennen, en we hebben een straal nodig, hebben we een formule (of vergelijking) nodig voor straal in termen van oppervlakte (in wat volgt, houd het doel van een formule in gedachten). De oppervlakte van de cirkel is P * r2 (r2 betekent r kwadraat, en * betekent vermenigvuldigen) de oppervlakte van de overgebleven secties buiten de driehoeken, maar binnen de cirkel (een gebied dat we al niet 6*P zijn), kan ook worden gevonden door de oppervlakte van de driehoeken af te trekken van de oppervlakte van de cirkel. We moeten een gebied van één van de gelijkzijdige driehoeken vinden.
Methode 1 Voor het berekenen van een oppervlakte van een driehoek
is de oppervlakte van een driehoek b*h/2 Dit is waar enige trigonometrie nodig is: teken een lijn van een hoekpunt naar een tegenoverliggende zijde die de tegenoverliggende zijde in tweeën deelt en loodrecht is. Dit verdeelt de gelijkzijdige driehoek in twee gelijke rechthoekige driehoeken, en de nieuwe zijde is de hoogte, noem het h. We moeten zoeken naar h.
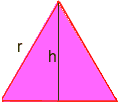
met Behulp van trigonometrie in één van de rechthoekige driehoeken, we hebben sin60 = h/r, Maar sin60 = sqr(3)/2, waar sqr(3): de wortel van drie sqr(3)/2 = h/r vermenigvuldig beide zijden door r om h = r*sqr(3)/2 r Nu, de oppervlakte van een gelijkzijdige driehoek is b*h/2 = (r)*(r*sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6*sqr(3)/4)) Gebruik de volgorde van bewerkingen te berekenen op een rekenmachine (met P=3.14): r= 5.896… De straal van de cirkel is dus ca. 5.9. Paul