Het zonnestelsel: de Aarde En De Maan
de planeten zijn tientallen en honderden miljoenen kilometers van ons verwijderd. Om het gebruik van zulke grote aantallen te vermijden, wordt de astronomische eenheid (AU) aangenomen als de eenheid van afstand, dat wil zeggen, De gemiddelde afstand tussen de aarde en de zon, 149.600.000 km.Licht duurt 8 minuten en 19 seconden om deze afstand af te leggen.
de grootte van het zonnestelsel overschrijdt de baan van Pluto op 40 AE en wordt gedefinieerd als een baan waarin de aantrekkingskracht van de zon gelijk is aan de aantrekkingskracht van de sterren die het dichtst bij ons staan. De afmetingen van het zonnestelsel zou dan in de Orde van 1.5 105 ae. Het is duidelijk dat deze dimensies erg klein zijn in vergelijking met de dimensies van het sterrenstelsel of het zichtbare universum. De eenheden die worden genomen om deze enorme afstanden te meten zijn de lichtjaar en de parsec die gelijk is aan 206 265 AU of 3,26 lichtjaar.De planeten van het zonnestelsel zijn verdeeld in twee groepen: de aardse groep gevormd door Mercurius, Venus, Aarde en Mars en de reuzenplaneten groep gevormd door Jupiter, Saturnus, Uranus en Neptunus.
alle planeten behalve Venus en Mercurius hebben satellieten, waarvan de meeste tot de reuzenplaneten behoren. De aarde, Jupiter, Saturnus en Neptunus hebben de grootste satellieten: de maan, de satellieten van Jupiter ontdekt door Galileo (Io, Europa, Ganymedes, Callisto), de satelliet Titan van Saturnus en Triton van Neptunus. Asteroïden bezetten een groot ringvormig gebied tussen de banen van Mars en Jupiter, op een gemiddelde afstand van 2,75 AE van de zon. De grootste asteroïde is Ceres met een diameter van 1000 km.
kometen, die ongeveer 600 zijn gecatalogiseerd, zijn onderverdeeld in twee groepen: korte periode (minder dan 20 jaar) en lange periode (meer dan 20 jaar). Er zijn verschillende hypothesen over de oorsprong van kometen, waaronder die van de Nederlandse astronoom J. Oort.
naast de in de interplanetaire ruimte genoemde lichamen is er een groot aantal deeltjes van verschillende grootte, voornamelijk die met een massa van duizendsten of miljoensten van een gram, die meteorisch stof worden genoemd. De vorming van deze deeltjes is waarschijnlijk te wijten aan de botsing van grotere lichamen (asteroïden) en hun opeenvolgende fragmentatie gedurende het bestaan en de evolutie van het zonnestelsel.
Meteorisch stof is verantwoordelijk voor het verschijnsel van zodiakaal licht, dat wordt waargenomen na zonsondergang of voor dageraad, als gevolg van de verspreiding van licht door deze stofdeeltjes. De meeste deeltjes verdampen wanneer ze de atmosfeer van de aarde binnenkomen (op hoogtes tussen 80 en 120 km), waarbij slechts een klein deel het aardoppervlak bereikt.
Laten we nu eens kijken naar enkele gegevens in verband met de planeten van het zonnestelsel
Eerste van de Zon
| hemellichaam | Radio | Massa |
|---|---|---|
| Zon | 6.96·108 m | 1.98·1030 kg |
Dan, uit het Land
| hemellichaam | semi-grote-as | Periode | Massa |
|---|---|---|---|
| Aarde | 149.6·109 m | 1 jaar=365.26 dagen | 5.98·1024 kg |
en de rest van de planeten
| Planeet | halve lange as (AU) | Excentriciteit | Periode (jaar) | Massa |
|---|---|---|---|---|
| Kwik | 0.387 | 0.206 | 0.24 | 0.06 |
| Venus | 0.723 | 0.007 | 0.62 | 0.82 |
| Aarde | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturnus | 9.539 | 0.056 | 29.46 | 95.1 |
| Uranus | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptunus | 30.058 | 0.009 | 164.8 | 17.2 |
In de volgende tabel zijn bedoeld als aanvullende gegevens:
- de helling van het vlak van de baan van de planeet ten opzichte van de ecliptica (vlak van de baan van de aarde))
- de rotatieperiode rond zijn as. Het was erg moeilijk om deze magnitude te meten voor planeten als Mercurius en Venus. De gasvormige schillen van Jupiter, Saturnus, Uranus en Neptunus bezitten de eigenschap van differentiële rotatie, dat wil zeggen dat hun rotatieperioden variëren afhankelijk van de breedtegraad.
- de helling van de draaias ten opzichte van het vlak van de baan. In het geval van Venus is het 177º wat gelijk staat aan het zeggen dat de helling van de as 3º is, maar de draairichting is omgekeerd. Hetzelfde argument geldt voor Uranus, wat aangeeft dat de rotatieas van Uranus zich bijna in het vlak van zijn baan bevindt.
| planeet | hellingshoek van de baan | draaiperiode | dichtheid g / cm3 | Radio-evenaar (km) | ashoek | No. van satellieten |
|---|---|---|---|---|---|---|
| kwik | 7e.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Venus | 3rd.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| Aarde | 0 | 23u.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1st. 8 | 24h.6 | 3.95 | 3 394 | 25º.2 | 2 |
| Jupiter | 1st. 3 | 9h.9 | 1.33 | 71 398 | derde.1 | 16 |
| Saturnus | 2nd.5 | 10h.2 | 0.69 | 60 000 | 26º.4 | 17 |
| Uranus | 0º.8 | 10u.8 | 1.26 | 25 400 | 98º | 5 |
| Neptunus | 1e.8 | 15u.8 | 1.67 | 24 750 | 29º | 2 |
satellieten
ten slotte verschaffen wij enkele gegevens over de belangrijkste satellieten van de planeten. Jupiter en Saturnus hebben veel satellieten die veel groter zijn dan die van Mars, maar we noemen alleen die die vergelijkbaar zijn in grootte of groter dan onze maan.
| Planeet | Satellieten | Dichtheid g/cm3 | Straal (km) | Radio baan (103 km) | Periode (dagen) |
|---|---|---|---|---|---|
| Aarde | Maan | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturnus | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptunus | Newt | 2 200 | 394.7 | 5.84 |
activiteiten
- bepalen de massa van de planeet Jupiter aan de hand van de radiogegevens en de omwentelingsperiode van een van zijn satellieten.
- Bepaal de straal van de baan van een satelliet van de planeet Jupiter uit de massa van die planeet en de omwentelingsperiode van de satelliet.
- Bepaal de intensiteit van het zwaartekrachtveld g op het oppervlak van de planeten en sommige satellieten, aan de hand van de gegevens van hun massa M en hun straal R of hun dichtheid ρ en hun straal.
voorbeeld: bepaal de massa van de planeet Jupiter in de wetenschap dat de straal van Io ‘ s Baan 421.600 km is en dat de omwentelingsperiode 1.769 dagen bedraagt. Feit: de constante G is 6,67 * 10-11 Nm2 / kg2
voorbeeld: Bereken de straal van de baan van de satelliet Callisto wetende dat de omwentelingsperiode is 16.689 dagen en de massa van de planeet Jupiter is 1.901·1027 kg. Gegevens: de constante G is 6,67 * 10-11 Nm2 / kg2
G = G M R 2 = 4π 3 GPR
gegevens: de constante G is 6.67 * 10-11 Nm2 / kg2
de maan
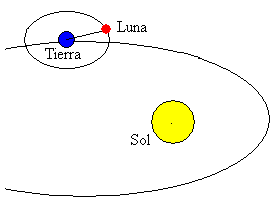
de maan is een van de grootste hemellichamen in het zonnestelsel. Zijn baan is bijna cirkelvormig (excentriciteit ε = 0,05) en het vlak van zijn baan is 5º hellend ten opzichte van het vlak van de baan van de aarde.De gemiddelde afstand tussen het centrum van de aarde en de maan is 384.400 km.De rotatieperiode rond de aarde is 27.322 dagen. De verandering van de positie van de maan ten opzichte van de zon geeft aanleiding tot de fasen van de maan.
de maan presenteert altijd hetzelfde gezicht aan de aardse waarnemer, vanwege het effect van de getijdekrachten die de aarde uitoefent op de maan. Dat betekent dat de rotatieperiode van de maan om zijn as samenvalt met de tijd die nodig is om een baan rond de aarde te voltooien.
de maan is het hemellichaam dat de mens het meest heeft gefascineerd. De voormalige Sovjet-Unie stuurde voor het eerst een automatisch schip dat in 1959 op het maanoppervlak landde. Op 20 juli 1969 waren Neil Armstrong en Edwin Aldrin de eerste mannen die op het maanoppervlak liepen als onderdeel van de Apollo 11-missie. Het Laatste bezoek van Amerikaanse astronauten aan de maan vond plaats in 1972.
de oorsprong van de maan lijkt onzeker, er zijn verschillende theorieën:
-
het werd gevormd op hetzelfde moment de aarde met het materiaal van een nevel
-
een hemellichaam is verdeeld in twee delen, waardoor de aarde en de maan ontstaan
-
dat de maan elders werd gevormd en door de aarde werd gevangen
-
dat de aarde botste met een hemellichaam van grote omvang (ongeveer ter grootte van Mars of groter), en dat de maan werd gevormd met het materiaal dat uit deze botsing werd verdreven.
deze laatste theorie lijkt op dit moment de meest geaccepteerde door de wetenschappelijke gemeenschap.
maanpad
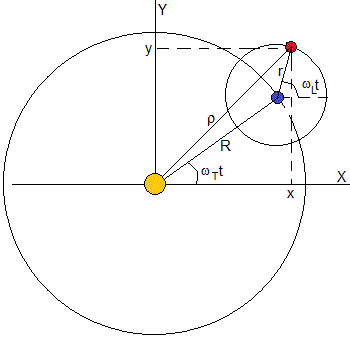
denk aan een planeet en zijn satelliet. De planeet beschrijft een cirkelbaan van straal R rond zijn ster met constante hoeksnelheid wT=2π/PT, waarbij PT de periode of tijd is die tot een volledige draai leidt. De satelliet beschrijft een cirkelvormige baan coplanaria van straal r met constante hoeksnelheid wL=2π/PL, PL wordt de periode of de tijd die het kost om een complete revolutie
de positie van de satelliet met betrekking tot een referentie-systeem waarvan de oorsprong is van de ster, is
x=Rcos( ω T )+rcos( ω L, t ) y=Risiko( ω T )+risiko( ω L, t )
α=wT/wL
{ x=Rcos( α ω L, t )+rcos( ω L, t ) y=Risiko( α ω L, t )+risiko( ω L, t ) { x=Rcos( α 2π P L t )+rcos( 2π P L t ) y=Risiko( α 2π P L t )+risiko( 2π P L t )
wij Bellen τ=t/PL
x R = cos( α·2πτ )+ r R cos( 2πτ ) en R =sin( α·2πτ )+ r r sin (2πτ )
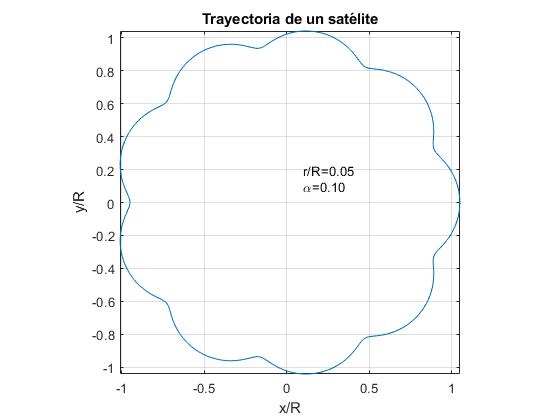
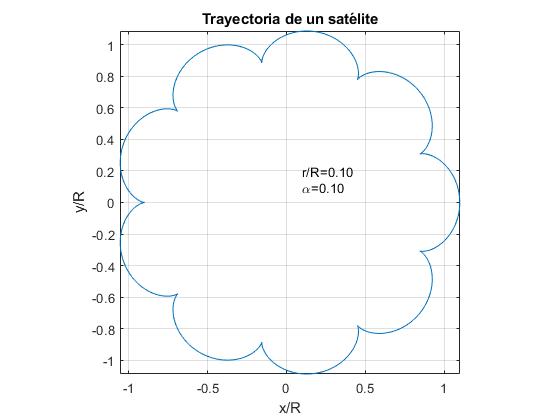
Wij vertegenwoordigen de baan van een satelliet Voor α=0,1 en voor drie waarden van de verhouding r/R.
- r/r<α. Voorbeeld: r / R = 0,05
- r/R = α. Voorbeeld: r / R = 0,1
- r / R > α. Voorbeeld, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
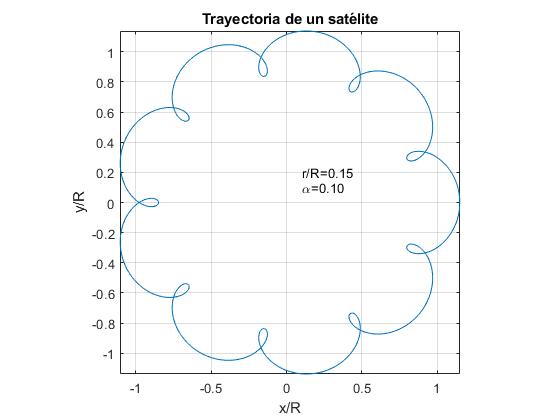
voor het geval van de aarde en de maan zijn de gegevens:
- straal van de baan van de maan: r = 384,4 * 106 m, periode PL = 27.32 d
- straal van de baan van de aarde: R = 149,6 * 109 m, periode PT = 365,26 d
α = wT / wL=PL / PT = 0,0748. r / R=0,0026
de baan van de maan zal op het eerste cijfer lijken. In de grafische voorstelling van de baan van de Maan voor deze waarden van α en r/R niet genieten van de oscillaties van de radiale afstand tussen de Zon en de Maan
Versnelling van de Maan
De afstand ρ van de Zon naar de Maan, is
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )
wij Berekenen de rechthoekige componenten van de versnelling
{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L, t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L, t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L, t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L, t )
de radiale component van De versnelling
te ρ = a → · ρ → ρ = a x x+ y x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2 rr cos ( ω L − ω T )t )
De minimale en maximale waarden worden verkregen wanneer cos((wL-wT)t)=±1
een max = ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
de maan is de enige satelliet in het zonnestelsel, waarvan de radiale component van de versnelling negatief is, er wordt gezegd dat ‘de maan naar de zon valt,’
fasen van de maan
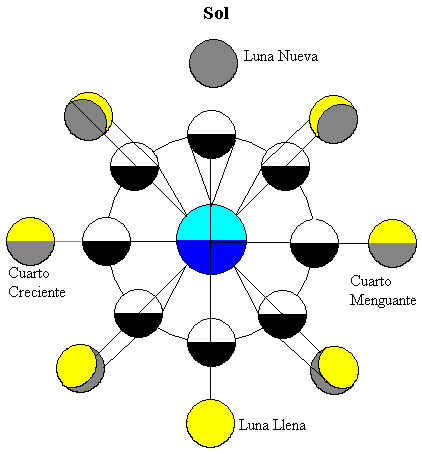
de figuur toont de Maan in verschillende posities in zijn baan rond de aarde. De zon is ver weg en verlicht beide hemellichamen (bovenaan de figuur)
de helft van de maan wordt verlicht door de zon (in witte kleur) en de helft van de maan die het dichtst bij de Aarde staat is zichtbaar voor aardse waarnemers. Als de maan rond de aarde beweegt zien we verschillende fracties van het deel verlicht door de zon (de gele gebieden).
-
wanneer de maan tussen de aarde en de zon staat, is het gedeelte van de maan dat het dichtst bij de Aarde staat donker, dus we kunnen de maan niet zien, deze fase wordt de nieuwe maan genoemd.
-
wanneer de aarde zich tussen de zon en de Maan bevindt, is het deel van de maan dat het dichtst bij de Aarde staat de verlichte helft, deze fase wordt volle maan genoemd.
-
wanneer de Maan in tussenstand staat, wordt slechts de helft van het dichtstbijzijnde deel van de aarde verlicht. Daarom zien we slechts een kwart van de Maan, deze twee fasen worden kwartalen genoemd, die toenemen of afnemen afhankelijk van de vraag of het verlichte deel dat zichtbaar is vanaf de aarde de neiging heeft te groeien of af te nemen.
opmerking: Dit interactieve programma probeert de fasen van de maan te verklaren, maar het is een getrouwe weergave van de baan van de maan, die een hoek van 5 ° vormt met het vlak van de ecliptica (de baan van de aarde rond de zon), of de oriëntatie van de as van de aarde die ongeveer 23º is met het normale vlak ten opzichte van het vlak van de ecliptica.
er is een rode lijn over de maan getrokken, zodat de lezer het samenvallen van de rotatieperiode van de maan rond zijn as en de tijd die nodig is om een baan rond de aarde te voltooien, kan begrijpen.
maansverduisteringen
maansverduisteringen treden op wanneer de Maan in volle fase is en wanneer de zon, de aarde en de Maan in een rechte lijn staan. Dan is de Maan in de schaduw geproduceerd door de aarde zoals weergegeven in de figuur.
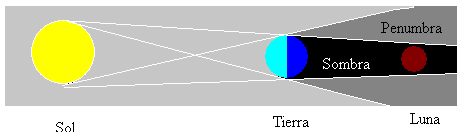
er zijn andere soorten maansverduisteringen, die afhankelijk zijn van de uitlijning van de drie hemellichamen. De maan kan in een onverlichte zone (schaduw) of gedeeltelijk verlicht zijn (penumbra).
de zonsverduistering treedt op wanneer de maan tussen de zon en de Aarde staat, de maan is in een nieuwe fase. De maan is 400 keer kleiner dan de zon maar de maan is 400 keer dichter bij de aarde, dus de schijnbare grootte van beide lichamen gezien vanaf de aarde is bijna hetzelfde. De maan kan aldus een totale zonsverduistering veroorzaken, indien waargenomen in de schaduwzone die door de Maan op aarde wordt geprojecteerd.
Maangegevens
| massa (kg)) | 7.349·1022 |
| straal (km) | 1737. 4 |
| gemiddelde dichtheid (g / cm3) | 3.34 |
| gemiddelde Afstand tot de Aarde (km) | 384 000 |
| Periode van baan (dagen) | 27.32166 |
| Versnelling van de zwaartekracht aan de evenaar (m/s2) | 1.62 |
| Eccentriciteit van de baan | 0.0549 |
| Hellingshoek van de baan (graden) | 5.1454 |
-
Bereken de straal van de cirkelvormige baan van de Maan rond de Aarde in de wetenschap dat de periode is 27.32 dagen. Bereken ook de snelheid van de maan. Gegevens: G = 6,67 * 10-11 Nm2 / kg2, de massa van de aarde is M = 5,98 * 1024 kg.
-
Bereken de versnelling van zwaartekracht g op het oppervlak van de maan.
-
Bereken het quotiënt tussen de diameter van de zon en de diameter van de maan. Bereken de verhouding tussen de gemiddelde afstand tussen de zon en de Aarde, En De Maan en de aarde. Gegevens: zonradius 6,96 * 108 m, Midden aarde-Zonafstand 1,49 * 1011 m
-
Bereken de positie van het middelpunt van de massa van het Aarde-Maansysteem, gemeten vanaf het centrum van de aarde.
-
Bereken de aantrekkingskracht van de aarde op de maan, vergelijk het met de aantrekkingskracht van de zon op de maan. Datum: zon massa, 1.98 * 1030 kg
referenties
M. Marov. Planeten van het zonnestelsel. Uitgeverij Mir.
meer informatie over planeten in hoeveel planeten zijn er in ons zonnestelsel?. ComofuncionaQue.com
voor het gedeelte ‘baan van de maan’
David C. Johnston. Cycloïdale paden in de fysica als superposities van translationele en rotatiebewegingen. Is. J. Phys.87 (10), oktober 2019, PP.808-810
de maan draait altijd naar de zon. Wiskundepagina ‘ s.