logaritmen gebruiken in de echte wereld
logaritmen zijn overal. Gebruik je ooit de volgende zinnen?
- 6 cijfers
- dubbele cijfers
- orde van grootte
- rente
u beschrijft getallen in termen van hun bevoegdheden van 10, een logaritme. En een rente is de logaritme van de groei van een investering.
verrast dat logaritmen zo vaak voorkomen? Ik ook. De meeste pogingen tot wiskunde in de echte wereld (TM) wijzen op logaritmen in een geheimzinnige formule, of doen alsof we geologen zijn die gefascineerd zijn door de schaal van Richter. “Wetenschappers geven om houtblokken, en dat zou jij ook moeten doen. Kun je je een wereld zonder zink voorstellen?”
nee, nee, nee, nee nee, nee nee! (Mama mia!)
Math drukt concepten uit met notatie zoals “ln”of ” log”. Het vinden van “wiskunde in de echte wereld” betekent het ontmoeten van ideeën in het leven en zien hoe ze kunnen worden geschreven met notatie. Kijk niet naar de letterlijke symbolen! Wanneer heb je voor het laatst een division teken geschreven? Wanneer heb je voor het laatst wat eten gehakt?
Ok, ok, we snappen het: waar gaan logaritmen over?
logaritmen vinden de oorzaak voor een effect, dat wil zeggen de invoer voor sommige uitvoer
een veel voorkomend “effect” is het zien van iets groeien, zoals van \$100 naar \$150 in 5 jaar. Hoe is dit gebeurd? We weten het niet zeker, maar de logaritme vindt een mogelijke oorzaak: een continue return van ln(150/100) / 5 = 8,1% zou verantwoordelijk zijn voor die verandering. Het is misschien niet de werkelijke oorzaak (is alle groei gebeurd in het laatste jaar?), maar het is een glad gemiddelde dat we kunnen vergelijken met andere veranderingen.
tussen haakjes, het begrip “oorzaak en gevolg” is genuanceerd. Waarom is 1000 groter dan 100?
- 100 is 10 die door zichzelf groeide gedurende 2 tijdsperioden ($10 * 10$)
- 1000 is 10 die door zichzelf groeide gedurende 3 tijdsperioden ($10 * 10 * 10$)
we kunnen getallen zien als uitgangen (1000 is “1000 uitgangen”) en ingangen (“hoe vaak moet 10 groeien om die uitgangen te maken?”). Dus,
1000 outputs > 100 outputsomdat
3 inputs > 2 inputsof met andere woorden:
log(1000) > log(100)Waarom is dit nuttig?
logaritmen zetten getallen op een menselijke schaal.
grote aantallen breken onze hersenen. Miljoenen en biljoenen zijn” echt groot ” ook al is een miljoen seconden 12 dagen en een biljoen seconden is 30.000 jaar. Het is het verschil tussen een Amerikaans vakantiejaar en de hele menselijke beschaving.
de truc om “enorme getalblindheid” te overwinnen is om getallen te schrijven in termen van “inputs” (d.w.z. hun machtsbasis 10). Deze kleinere schaal (0 tot 100) is veel gemakkelijker te begrijpen:
- power van 0 = $10^0$ = 1 (één item)
- power van 1 = $10^1$ = 10
- macht 3 = $10^3$ = duizend
- voeding 6 = $10^6$ = eur
- kracht van 9 = $10^9$ = miljard
- macht 12 = $10^12$ = biljoen
- macht 23 = $10^23$ = aantal moleculen in een dozijn gram koolstof
- power van 80 = $10^80$ = aantal moleculen in het heelal
Een 0-80 schaal bracht ons van een enkel item van het aantal zaken in het heelal. Niet slecht.
logaritmen tellen vermenigvuldiging als stappen
logaritmen beschrijven veranderingen in termen van vermenigvuldiging: in de voorbeelden hierboven is elke stap 10x groter. Met de natuurlijke log is elke stap ” e ” (2.71828…) keer meer.
bij het omgaan met een reeks van vermenigvuldigingen helpen logaritmen om ze te “tellen”, net zoals optellen voor ons telt wanneer effecten worden toegevoegd.
toon me de wiskunde
tijd voor het vlees: laten we eens kijken waar logaritmen verschijnen!
salaris met zes cijfers of uitgaven met twee cijfers
we beschrijven getallen in termen van hun cijfers, d.w.z. hoeveel krachten van 10 ze hebben (zijn ze in de tientallen, honderden, duizenden, tienduizend, enz.). Een cijfer toevoegen betekent “vermenigvuldigen met 10”, d.w.z.
![]()
logaritmen tellen het aantal toegevoegde vermenigvuldigingen, dus beginnend met 1 (een enkel cijfer) voegen we nog 5 cijfers toe ($10^5$) en 100.000 krijgen een 6-cijferig resultaat. Praten over” 6 “in plaats van” honderdduizend ” is de essentie van logaritmen. Het geeft een ruw gevoel van schaal zonder te springen in de details.
bonusvraag: hoe zou u 500.000 beschrijven? “6 cijfers” zeggen is misleidend omdat 6 cijfers vaak iets in de buurt van 100.000 betekenen. Zou “6,5 cijfer” werken?
niet echt. In ons hoofd betekent 6.5 “halverwege” tussen 6 en 7 cijfers, maar dat is de mentaliteit van een adder. Met logaritmen a”.5 ” betekent halverwege in termen van vermenigvuldiging, dat wil zeggen de vierkantswortel ($9^.5$ betekent de vierkantswortel van 9 — 3 is halverwege in termen van vermenigvuldiging omdat het 1 tot 3 en 3 tot 9 is).
als we log(500.000) nemen krijgen we 5.7, Tel 1 op voor het extra cijfer, en we kunnen zeggen “500.000 is een 6.7 cijfer nummer”. Probeer het hier uit:
orde van grootte
wij geeks houden van deze zin. Het betekent ruwweg “10x verschil” maar klinkt gewoon koeler dan “1 cijfer groter”.
in computers, waar alles wordt geteld met bits (1 of 0), heeft elk bit een verdubbeling effect (niet 10x). Dus gaan van 8 naar 16 bits is “8 ordes of magnitude” of $2^8 = 256$ keer groter. (“Groter” verwijst in dit geval naar de hoeveelheid geheugen die kan worden aangepakt.) Gaan van 16 naar 32 bits betekent een extra 16 ordes van grootte, of $2^16$ ~ 65.536 keer meer geheugen dat kan worden aangepakt.
rente
hoe berekenen we de groeicijfers? Een land wil niet met 8,56% per jaar groeien. Je kijkt naar het BBP het ene jaar en het BBP het volgende, en neemt de logaritme om de impliciete groei te vinden.
mijn twee favoriete interpretaties van de natuurlijke logaritme (ln (x)), dat wil zeggen de natuurlijke logaritme van 1.5:
- uitgaande van 100% groei, hoe lang heb je nodig om te groeien tot 1,5? (.405, minder dan de helft van de tijdsperiode)
- uitgaande van 1 tijdseenheid, hoe snel moet u groeien om tot 1,5 te komen? (40.5% per jaar, continu samengesteld)
logaritmen zijn hoe we erachter komen hoe snel we groeien.
meetschaal: Google PageRank
Google geeft elke pagina op het web een score (PageRank) die een ruwe maat is voor Autoriteit / belang. Dit is een logaritmische schaal, wat in mijn hoofd betekent “PageRank telt het aantal cijfers in uw score”.
een site met pagerank 2 (“2 cijfers”) is 10x populairder dan een site met PageRank 1. Mijn site is PageRank 5 en CNN heeft PageRank 9, dus er is een verschil van 4 ordes van grootte ($10^4$ = 10,000).
ongeveer 7000 bezoeken per dag. Met behulp van mijn envelop wiskunde, Ik kan raden CNN krijgt ongeveer 7000 * 10.000 = 70 miljoen bezoeken / dag. Hoe heb ik dat gedaan? In mijn hoofd denk ik $7k * 10k = 70 * k * k = 70 * M$). Ze kunnen een paar keer meer dan dat (100M, 200M), maar waarschijnlijk niet tot 700M.
Google brengt veel informatie met een zeer ruwe schaal (1-10).
meetschaal: Richter, Decibel, enz.
zucht. We zijn bij de typische “logaritmen in de echte wereld” voorbeeld: Richter schaal en Decibel. Het idee is om gebeurtenissen die drastisch kunnen variëren (aardbevingen) op een enkele schaal met een klein bereik (meestal 1 tot 10). Net als PageRank, elke 1-punt verhoging is een 10x verbetering van de macht. De grootste menselijke aardbeving was 9,5; de impact op het schiereiland Yucatán, waardoor de dinosaurussen waarschijnlijk uitgestorven waren, was 13.
Decibels zijn vergelijkbaar, hoewel het negatief kan zijn. Geluiden kunnen gaan van intens stil (pindrop) tot extreem luid (vliegtuig) en onze hersenen kunnen het allemaal verwerken. In werkelijkheid is het geluid van de motor van een vliegtuig miljoenen (miljarden, biljoenen) keer krachtiger dan een pindrop, en het is lastig om een schaal te hebben die van 1 naar een triljoen gaat. Logs houden alles op een redelijke schaal.
logaritmische grafieken
u ziet vaak items uitgezet op een”logschaal”. In mijn hoofd betekent dit dat één kant “aantal cijfers” of “aantal vermenigvuldigingen” telt, niet de waarde zelf. Nogmaals, dit helpt tonen Wild variërende gebeurtenissen op een enkele schaal (gaande van 1 tot 10, niet 1 tot miljarden).
de wet van Moore is een goed voorbeeld: we verdubbelen het aantal transistors om de 18 maanden (figuur met dank aan Wikipedia).
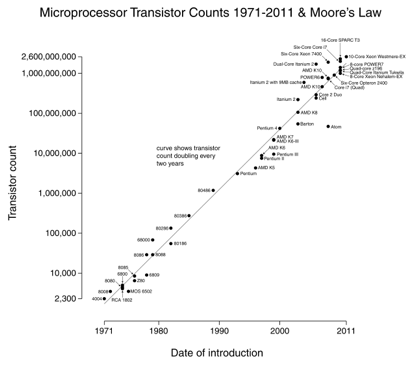
het leuke van log-schaal grafieken is dat exponentiële veranderingen (processorsnelheid) verschijnen als een rechte lijn. Groeien 10x per jaar betekent dat je gestaag marcheren de “cijfers” schaal.
voorwaarts en omhoog
als een concept bekend maar niet geliefd is, betekent dit dat we onze intuïtie moeten opbouwen. Vind de analogieën die werken, en neem geen genoegen met de slop een leerboek zal Draven. In mijn hoofd:
- logaritmen vinden de oorzaak van een effect (zie groei, rente vinden)
- ze helpen vermenigvuldigingen of cijfers te tellen, met de bonus van partiële tellingen (500k is een 6,7 cijferig getal))
fijne wiskunde.
andere posten in deze reeks
- an Intuã tive Guide To Exponential Functions & e
- Demystifying the Natural logaritme (ln)
- a Visual Guide to Simple, Compound and Continuous Interest Rates
- Common Definitions of e (Colorized)
- Understanding Exponents (Why does 0^0 = 1?)
- logaritmen gebruiken in de echte wereld
- hoe te denken met exponenten en Logaritmen
- Discrete Versus continue groei
- wat betekent een exponent werkelijk?
- Q: Waarom is e speciaal? (2.718… niet 2, 3,7 of een ander getal?)