Nee, wetenschappers zullen nooit in staat zijn om de lege ruimte van atomen te verwijderen

BY admin
|

als je een object in het universum zou nemen dat gemaakt is van normale materie — alles wat een mens zou kunnen aanraken, zien of anderszins een interactie met het gebruik van ons lichaam zou kunnen detecteren — dan zou je ontdekken dat je het zou kunnen opsplitsen in steeds kleinere componenten. Een heel menselijk lichaam kan worden opgesplitst in organen, die op hun beurt zijn opgebouwd uit cellen. Elke cel bestaat uit organellen, die kleinere structuren met gespecialiseerde functies zijn, en organellen zijn afhankelijk van interactie die op het moleculaire niveau voorkomen.

waaruit de volledige reeks moleculen bestaat, zijn atomen: de kleinste component van normale materie die het individuele karakter en de eigenschappen van het betrokken element behoudt. Elementen worden gedefinieerd door het aantal protonen in de kern van elk atoom, waarbij een atoom bestaat uit elektronen die rond die kern cirkelen. Maar ondanks het feit dat atomen meestal lege ruimte binnenin zijn, is er geen manier om die ruimte te verwijderen. Hier is het verhaal waarom.

van macroscopische schalen tot subatomaire, de grootte van de fundamentele deeltjes spelen slechts een kleine rol in het bepalen van de grootte van composietstructuren. In plaats daarvan zijn het de krachtwetten en hoe ze interageren tussen deeltjes beïnvloed door die interacties (of geladen onder hen) en die bepalen hoe meer fundamentele structuren zich verbinden om grotere structuren op te bouwen. (MAGDALENA KOWALSKA / CERN / ISOLDE TEAM))

een atoom, op het meest basale niveau, bestaat uit een positief geladen atoomkern die extreem klein is in volume. Voor elk proton in de atoomkern, is er een gelijke en tegenovergestelde kwantum van lading die eromheen draait, waardoor een totaal neutraal systeem ontstaat: het elektron.

maar terwijl de atoomkern beperkt is tot een uiterst klein volume — de diameter van een proton is ongeveer 1 femtometer, of 10^-15 m — nemen de elektronen, die zelf puntachtige deeltjes zijn, een volume in dat ongeveer 1 ångstrom (10^-10 m) in alle drie dimensies bedraagt.Het eerste experiment dat dit enorme verschil aantoonde is meer dan een eeuw oud, toen de natuurkundige Ernest Rutherford een dunne plaat goudfolie bombardeerde met radioactieve deeltjes.

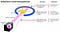
Rutherford ‘ s gold foil experiment toonde aan dat het atoom grotendeels lege ruimte was, maar dat er een concentratie van massa op een bepaald punt was die veel groter was dan de massa van een alfadeeltje: de atoomkern. (CHRIS IMPEY))

wat Rutherford deed was eenvoudig en duidelijk. Het experiment begon met een ringvormig apparaat ontworpen om deeltjes te detecteren die het vanuit elke richting tegenkomen. In het midden van de ring werd dun gehamerd goudfolie geplaatst met een dikte die zo klein was dat het niet gemeten kon worden met gereedschappen uit de vroege 20e eeuw: waarschijnlijk slechts een paar honderd of duizend atomen in doorsnede.Buiten zowel de ring als de folie werd een radioactieve bron geplaatst, zodat deze de goudfolie vanuit één bepaalde richting zou bombarderen. De verwachting was dat de uitgestoten radioactieve deeltjes de gouden folie zouden zien zoals een oplaadolifant een stuk zijdepapier zou zien: ze zouden er gewoon dwars doorheen gaan alsof de folie er helemaal niet was.

maar dit bleek alleen voor de meeste radioactieve deeltjes het geval te zijn. Een paar van hen — klein in aantal, maar van vitaal belang-gedroegen zich alsof ze stuiterde op iets hard en onbeweeglijk.

als atomen waren gemaakt van continue structuren, dan zouden alle deeltjes afgevuurd op een dunne plaat goud worden verwacht om dwars door het. Het feit dat harde recoils vrij vaak werden gezien, zelfs waardoor sommige deeltjes terugstuitten van hun oorspronkelijke richting, hielp illustreren dat er een harde, dichte kern inherent was aan elk atoom. (KURZON / Wikimedia COMMONS))

sommigen van hen verspreidden zich naar de ene of de andere kant, terwijl anderen leken terug te ketsen naar hun richting van oorsprong. Dit vroege experiment leverde het allereerste bewijs dat de binnenkant van een atoom niet een vaste structuur was zoals eerder voorzien, maar eerder bestond uit een extreem dichte, kleine kern en een veel meer diffuse buitenste structuur. Zoals Rutherford zelf opmerkte, terugkijkend decennia later,

“het was de meest ongelooflijke gebeurtenis die me ooit is overkomen in mijn leven. Het was bijna net zo ongelooflijk alsof je een 15-inch omhulsel afvuurde op een stuk papier en het kwam terug en raakte je.”

dit soort experimenten, waarbij je een laag, medium of hoog-energetisch deeltje afvuurt op een samengesteld deeltje, staat bekend als diepe inelastische verstrooiing, en het blijft onze beste methode om de interne structuur van elk systeem van deeltjes te onderzoeken.

als je twee deeltjes tegen elkaar botst, onderzoek je de interne structuur van de deeltjes die botsen. Als een van hen niet fundamenteel is, maar eerder een samengesteld deeltje is, kunnen deze experimenten zijn interne structuur onthullen. Hier is een experiment ontworpen om het donkere materie/nucleon verstrooiingssignaal te meten; diepe inelastische verstrooiingsexperimenten gaan zelfs tot op de dag van vandaag door. (DARK MATTER overzicht: COLLIDER, directe en indirecte detectie zoekopdrachten-QUEIROZ, FARINALDO S. ARXIV:1605.08788)

voor het atoom, van een eenvoudige zoals waterstof tot een complexe zoals goud, lood of uranium, kunnen de elektronen worden gevonden ver buiten de omvang van de atoomkern. Terwijl een atoomkern is beperkt tot een volume dat ongeveer 1 kubieke femtometer (10^-15 meter aan elke kant), kan een elektron worden gevonden verdeeld probabilistisch over een volume dat ongeveer een biljard (101⁵) keer groter. Deze eigenschap is onafhankelijk van welk element we beschouwen, het aantal aanwezige elektronen (zolang het tenminste één is), of welke methode we gebruiken om het elektron of de kern te meten.

het feit dat atomen meestal lege ruimte zijn, is vandaag de dag zelfs bekend bij de meeste schoolkinderen, die dit feit leren op ongeveer hetzelfde moment dat ze over de structuur van atomen leren. Bij het leren van dit, velen van hen vragen zich af — en ik weet zeker dat velen van jullie zich afvragen — waarom je niet gewoon die lege ruimte en compacte atomen kan verwijderen tot veel kleinere schalen, zoals de grootte van een atoomkern?

Waterstofdichtheid plotten voor een elektron in een verscheidenheid van kwantumtoestanden. Terwijl drie kwantumgetallen veel kunnen verklaren, moet’ spin ‘ worden toegevoegd om het periodiek systeem en het aantal elektronen in orbitalen voor elk atoom te verklaren. (POORLENO / Wikimedia COMMONS))

in de klassieke wereld, waar de natuur speelt volgens regels die we kennen en die overeenkomen met wat onze intuïtie voorspelt, is het heel gemakkelijk om de posities van deeltjes te controleren. Maar op kwantumniveau is er een fundamentele beperking ingesteld door de regels van de natuur: het Heisenberg onzekerheid Principe.

zelfs als je alles weet wat er te weten valt over een elektron dat om een atoomkern draait, inclusief:

  • welk energieniveau het inneemt,
  • wat de kwantumtoestand is,
  • en hoeveel andere elektronen er zijn in omringende energieniveaus,

er zal nog steeds een aantal eigenschappen die inherent onzeker zijn. In het bijzonder is een van de inherent onzekere eigenschappen de positie van het elektron; we kunnen alleen de kansverdeling uitrekenen van waar het elektron waarschijnlijk zal zijn.

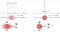
een illustratie tussen de inherente onzekerheid tussen positie en momentum op kwantumniveau. Er is een limiet aan hoe goed je deze twee hoeveelheden tegelijkertijd kunt meten, omdat het vermenigvuldigen van deze twee onzekerheden samen een waarde kan opleveren die groter moet zijn dan een bepaalde eindige hoeveelheid. Wanneer de ene nauwkeuriger bekend is, is de andere inherent minder in staat om met enige mate van betekenisvolle nauwkeurigheid gekend te worden. Dit concept is van toepassing op fase en amplitude voor gravitatiegolven. (E. SIEGEL / Wikimedia COMMONS gebruiker MASCHEN)

de reden hiervoor is de inherente kwantumonzekerheid tussen positie en momentum. Het momentum van een elektron, dat we kunnen zien als de bewegingseenheid die elk deeltje zal hebben, kan met een bepaalde precisie worden gekend door het uitvoeren van een specifieke meting.

echter, hoe nauwkeuriger uw momentum-onthullende meting is, hoe groter een inherente onzekerheid de handeling van het meten zal bijdragen aan de positie van het elektron. Omgekeerd, hoe nauwkeuriger je probeert de positie van het elektron te meten, hoe groter de onzekerheid die je veroorzaakt in het elektron ‘ s momentum zal zijn. Je kunt die twee grootheden — positie en momentum — slechts met een beperkte precisie tegelijkertijd kennen, omdat het nauwkeuriger meten van één een inherent grotere onzekerheid zal creëren in de ene die je niet meet.

als je een atoomkern neemt en er slechts één elektron aan bindt, dan zie je de volgende 10 waarschijnlijkheidswolken voor elk elektron, waarbij deze 10 diagrammen overeenkomen met het elektron dat elk van de 1s, 2s, 2p, 3s, 3P, 3d, 4s, 4p, 4d en 4f orbitalen, respectievelijk bezetten. Als je het elektron zou vervangen door een muon, zouden de vormen hetzelfde zijn, maar de lineaire omvang van elke dimensie zou ongeveer een factor 200 kleiner zijn. (GEEK3 / Wikimedia COMMONS)

het elektron neemt van nature het grote volume in dat we rond de atoomkern verwachten om twee redenen.

  1. de grootte van de waarschijnlijkheidswolk die het elektron inneemt is afhankelijk van de lading-massaverhouding van het elektron. Met dezelfde magnitude lading als het proton maar slechts 1 / 1836e van de massa, zelfs de ultra-sterke elektromagnetische kracht kan het elektron niet beperken tot een kleiner volume dan we zien.
  2. de uitwendige kracht die een elektron op een atoomkern drukt en de buitenste componenten van de waarschijnlijkheidswolk beperkt, is extreem klein, zelfs voor atomen die in een ultrasterk rooster aan elkaar zijn gebonden. De krachten tussen de elektronen in twee verschillende atomen, zelfs in atomen die aan elkaar gebonden zijn, zijn zeer klein in vergelijking met de kracht tussen de atoomkern en een elektron.

elk van deze redenen geeft ons de hoop op een oplossing die in de praktijk werkt, maar met beperkte toepasbaarheid.

of het nu in een atoom, molecuul of ion is, de overgangen van ronddraaiende deeltjes van een hoger energieniveau naar een lager energieniveau zullen resulteren in de emissie van straling bij een zeer specifieke golflengte. Als je de standaardomloopdeeltjes (elektronen) vervangt door zwaardere, onstabiele deeltjes (muonen), neemt de radiale grootte van het atoom af met ongeveer de massaverhouding van het zwaardere deeltje tot het lichtere deeltje, waardoor muonische atomen ~200 keer kleiner zijn in elk van de drie ruimtelijke dimensies dan standaard elektronische atomen. (GETTY IMAGES))

je kunt het elektron vervangen door een groter deeltje met dezelfde elektrische lading. Er zijn twee elektron-achtige deeltjes die in het standaardmodel bestaan met dezelfde lading als het elektron: de muon en de tau. Het muon is ongeveer 200 keer zo massief als een elektron, en dus is een atoom van muonic waterstof (met een proton voor een kern maar een muon in plaats van een elektron dat er omheen draait) ongeveer 200 keer kleiner dan standaard waterstof.

als je muonische waterstof bindt aan een aantal andere atomen, zullen ze dienen als katalysator voor kernfusie, waardoor het verder kan gaan met veel lagere temperaturen en energieën dan standaard fusie. Echter, muons leven slechts voor ~2 microseconden alvorens te vervallen, en de meer massieve Tau leeft voor minder dan een picoseconde. Deze exotische atomen zijn te vergankelijk om lang bruikbaar te blijven.

wanneer de brandstof van de lagere massa, zonachtige sterren opraakt, blazen ze hun buitenste lagen af in een planetaire nevel, maar het centrum trekt zich samen om een witte dwerg te vormen, wat heel lang duurt om te vervagen in het donker. De planetaire nevel die onze zon zal genereren zou volledig moeten verdwijnen, met alleen de witte dwerg en onze overgebleven planeten over, na ongeveer 9,5 miljard jaar. Soms worden objecten getidaliseerd en voegen stoffige ringen toe aan wat er over is van ons zonnestelsel, maar ze zullen van voorbijgaande aard zijn. De witte dwerg zal veel sneller roteren dan onze zon nu doet, maar met een verwachte massa van ongeveer 0,5 zonsmassa ‘ s, zullen de atomen in de kern van de witte dwerg, hoewel gecomprimeerd ten opzichte van de standaard atomen die we vandaag op aarde vinden, stabiel blijven. (MARK GARLICK / Universiteit van WARWICK)

als alternatief kun je de druk op de atomen enorm verhogen door ongelooflijke hoeveelheden massa op te stapelen op één enkele plaats in de ruimte. Een individueel atoom in isolatie is misschien slechts een ångstrom in grootte, maar als je de waarde van materiaal van een ster eromheen stapelt, zal dat atoom een externe druk voelen die het elektron “knijpt” om een veel beperkter volume in te nemen.

hoe groter de druk, hoe beperkender de elektronen zijn, en hoe kleiner de atomen zijn in termen van fysische omvang. Er is een limiet aan de externe druk die de atomen kunnen weerstaan voordat dezelfde catastrofe als eerder plaatsvindt: de atoomkernen komen zo dicht bij elkaar dat hun golffuncties elkaar overlappen en kernfusie kan plaatsvinden. Bij een witte dwerg komt deze drempel voor bij ongeveer 1,4 zonsmassa ‘ s; overschrijd deze, en je zult uiteindelijk een op hol geslagen fusiereactie initiëren, wat in dit geval resulteert in een type Ia supernova.

twee verschillende manieren om een type Ia-supernova te maken: het accretiescenario (L) en het fusiescenario (R). Zonder een binaire metgezel zou onze zon nooit supernova kunnen worden door materie aan te vullen, maar we zouden mogelijk kunnen fuseren met een andere witte dwerg in het melkwegstelsel, wat ons zou kunnen leiden tot revitalisering in een type Ia supernova explosie. Wanneer een witte dwerg een kritische (1,4 zonnemassa) drempel overschrijdt, zal kernfusie spontaan plaatsvinden tussen aangrenzende atoomkernen in de kern. (NASA / CXC / M. WEISS)

het zou een heerlijke science fiction droom om de lege ruimte te verwijderen uit atomen, het verminderen van het volume dat materie bezet met factoren van miljoenen, biljoenen of zelfs meer. Het is echter niet zo dat de elektronen die rond de kern cirkelen inherent een extreem groot volume ruimte innemen, maar eerder dat de kwantumeigenschappen die inherent zijn aan deeltjes — massa ‘ s, ladingen, interactiesterkte en kwantumonzekerheid — allemaal samenkomen om de atomen te creëren die in ons universum bestaan.

zelfs als we een stabiele, zwaardere tegenhanger van het elektron hadden, of de mogelijkheid om materie te comprimeren tot willekeurig dichte toestanden, zouden we een kwantumdrempel tegenkomen waar de atoomkernen in het centrum van atomen spontaan zouden fuseren, waardoor stabiele configuraties van meerdere atomen helemaal niet zouden bestaan. Het feit dat onze atomen meestal lege ruimte zijn, laat het bestaan van moleculen, chemie en leven toe.Het verwijderen van de lege ruimte uit atomen is misschien een leuk gedachte-experiment, maar atomen zijn zo groot als ze zijn vanwege de regels van het universum. Ons bestaan is afhankelijk van de aanwezigheid van die lege ruimte, maar met de constanten van de natuur hebben de waarden die ze doen, maak je geen zorgen. Het kan niet anders.