Bootstrap w R
Bootstrap jest metodą wnioskowania o populacji przy użyciu danych z próby.Bradley Efron wprowadził go po raz pierwszy w 1979 roku.Bootstrap polega na próbkowaniu z zastąpieniem z przykładowych danych. Technika ta może być użyta do oszacowania błędu standardowego dowolnej statystyki i uzyskania dla niej przedziału ufności (CI). Bootstrap jest szczególnie przydatny, gdy CI nie ma zamkniętej formy lub ma bardzo skomplikowaną.
Załóżmy, że mamy próbkę N elementów: X = {X1, x2,…, xn} i jesteśmy zainteresowani CI dla jakiejś statystyki T = T (X). Bootstrapframework jest prosty. Po prostu powtarzamy R razy następujący schemat: dla i-tego powtórzenia próbka z zamiennymi N elementami z próbki dostępnej (niektóre z nich zostaną wybrane więcej niż raz). Nazwij tonew sample I-TH Bootstrap sample, Xi, i calculatedesired statistic Ti = T(Xi).
w rezultacie otrzymamy wartości R naszych statystyk: T1, T2,…, TR. Nazywamy rozkładem Bootstrap T lub rozkładem bootstrap T. na jego podstawie możemy obliczyć CI dla T. istnieje kilka sposobów na to. Przyjmowanie percentyli wydaje się najłatwiejsze.
Bootstrap w akcji
użyjmy (jeszcze raz) znanego iris zbioru danych. Spójrz na pierwsze kilka wierszy:
Załóżmy, że chcemy znaleźć CIs dla mediany Sepal.Length, medianySepal.Width i współczynnika korelacji rang Spearmana między tymi dwoma. Użyjemy pakietu R boot i wywołanej funkcji… boot. Aby uzyskać jego moc, musimy stworzyć funkcję, która oblicza nasze statystyki z ponownie próbkowanych danych. Powinien mieć co najmniej dwa targumenty: dataset i Wektor zawierający indices elementów z zestawu danych, które zostały wybrane do utworzenia próbki bootstrap.
jeśli chcemy obliczyć CIs dla więcej niż jednej statystyki na raz, nasza funkcja musi zwrócić je jako pojedynczy wektor.
dla naszego przykładu może to wyglądać tak:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo wybiera żądane elementy (które liczby są przechowywane w indices)z data i oblicza współczynnik korelacji dwóch pierwszych kolumn (method='s' służy do wyboru współczynnika rang Spearmana,method='p' spowoduje współczynnik Pearsona) i ich mediany.
możemy również dodać kilka dodatkowych argumentów, np. pozwól użytkownikowi wybrać typ współczynnika korelacji:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}aby ten samouczek był bardziej ogólny, użyję drugiej wersjifoo.
teraz możemy użyć funkcji boot. Musimy podać jej nazwę oddataset, funkcję, którą właśnie stworzyliśmy, liczbę powtórzeń (R)i wszelkie dodatkowe argumenty naszej funkcji (jak cor.type). Poniżej Iuse set.seed dla powtarzalności tego przykładu.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funkcja zwraca obiekt klasy wywołanej… (tak, masz rację!)boot. Ma dwa ciekawe elementy. $t zawiera wartości R ourstatistic(s) wygenerowane przez procedurę bootstrap (realizacje bootstrap ofT):
$t0 zawiera wartości naszych statystyk w oryginalnym, pełnym, zbiorze danych:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000Drukowanie obiektu boot na konsoli daje dodatkowe informacje:
original jest taka sama jak $t0. bias jest różnicą między średnią realizacji Bootstrap (te z $t), zwaną estymatem bootstrap T i wartością w oryginalnym zbiorze danych (ten z $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error jest standardowym błędem oszacowania bootstrap, który odpowiada standardowemu odchyleniu realizacji bootstrap.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414różne typy bootstrap CIs
zanim zaczniemy od CI, zawsze warto rzucić okiem na dystrybucję realizacji bootstrap. Możemy użyć funkcji plot, zindex mówiącą, przy której ze statystyk obliczonych w foo chcemy się dowiedzieć. Tutaj index=1 jest współczynnikiem korelacji Spearmana między długością i szerokością, index=2 jest medianą długości od sepalu, aindex=3 jest medianą szerokości od sepalu.
plot(myBootstrap, index=1)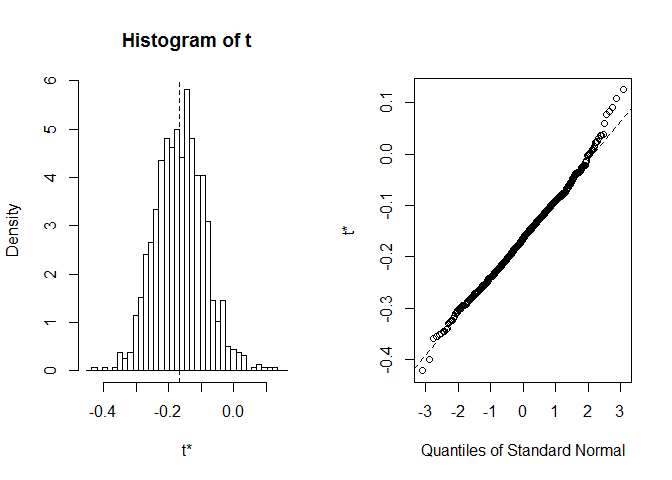
rozkład współczynników korelacji bootstrap wydaje się dość normalnopodobny. Znajdźmy informatora. Możemy użyć boot.ci. Domyślnie jest to 95-procentowy CIs, ale można go zmienić za pomocą parametru conf.
boot.ci zapewnia 5 typów CIs bootstrap. Jeden z nich, studentizedinterval, jest wyjątkowy. Potrzebuje oszacowania wariancji bootstrap. Nie podajemy go, więc R wypisuje Ostrzeżenie:bootstrap variances needed for studentized intervals. Wariancje można uzyskać za pomocą Bootstrapa drugiego poziomu lub (Łatwiej) Za pomocą techniki hackknife. Jest to w jakiś sposób poza zakresem tego samouczka, więc skupmy się na pozostałych czterech typach CIS bootstrap.
jeśli nie chcemy widzieć ich wszystkich, możemy wybrać odpowiednie w argumencie type. Możliwe wartości to norm, basic, stud, perc, bca Ora wektor tych.
funkcja boot.ci tworzy obiekt klasy… (tak, zgadłeś!)bootci. Jego elementy są nazywane tak jak typy CI używane w argumencie type. $norm jest 3-elementowym wektorem zawierającym poziom ufności i granice CI.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc i $bca są 5-elementowymi wektorami zawierającymi również percentyle używane do obliczania CI (wrócimy do tego później):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178trochę notacji (Przepraszam!)
aby zorientować się, czym są różne rodzaje CI, musimy wprowadzić notację. Więc niech:
- t⋆ być estymatem bootstrap (średnia bootstraprealizacji),
- T0 być wartością naszej statystyki w oryginalnym zbiorze danych,
- se⋆ być standardowym błędem estymatu bootstrap,
- B być odchyleniem estymatu bootstrapeb = t⋆ − t0
- α będzie poziomem ufności, zazwyczaj α = 0,95,
- za będzie $1-\frac \alpha 2$-kwantylem standardnormalnego rozkładu,
- θα będzie α-percentylem rozkładu bootstraprealizacji.
percentyl CI
z powyższą notacją, percentyl CI wynosi:
więc to wymaga odpowiednich percentyli. Nic więcej.
normalny CI
typowy Wald CI to:
ale w przypadku bootstrap, powinniśmy to skorygować pod kątem stronniczości. Tak więc staje się:
$$ t_0-b \pm z_ \ alpha \ cdot se^ \ star \ \ 2t_0-t^\star \ pm z_ \ alpha \cdot se^ \ star$$
podstawowy Ci
percentyl CI nie jest ogólnie zalecany, ponieważ działa słabo, gdy dochodzi do dziwnych rozkładów. Podstawowy CI (zwany także zbiorczym lub empirycznym CI) jest znacznie bardziej odporny na to. Celem jest obliczenie różnic pomiędzy poszczególnymi replikacjami bootstrap i t0 oraz wykorzystanie percentyli ich rozkładu. Fulldetails można znaleźć, np. we wszystkich statystykach L. Wassermana
końcowy wzór dla podstawowego CI to:
BCa CI
BCA pochodzi z biasu-poprawione, przyspieszone. Wzór nie jest zbyt skomplikowany, ale nieco nieintuicyjny, więc pominę go.Zobacz artykuł Tomasza J. DiCiccio i BradleyEfron, jeśli interesują Cię szczegóły.
przyspieszenie wymienione w nazwie metody wymaga użycia specyficznych wartości realizacji bootstrap. Czasami może się zdarzyć, że będą to jakieś skrajne percentyle, ewentualnie wartości odstające.BCa może być niestabilny w takich przypadkach.
spójrzmy na BCa CI dla mediany szerokości płatka. W pierwotnym zbiorze danych mediana ta równa się dokładnie 3.
otrzymujemy BCA CI (2.9, 2.9). To dziwne, ale na szczęście Rostrzegł nas, że extreme order statistics used as endpoints. Zobaczmy, co dokładnie się tu wydarzyło.:
plot(myBootstrap, index=3)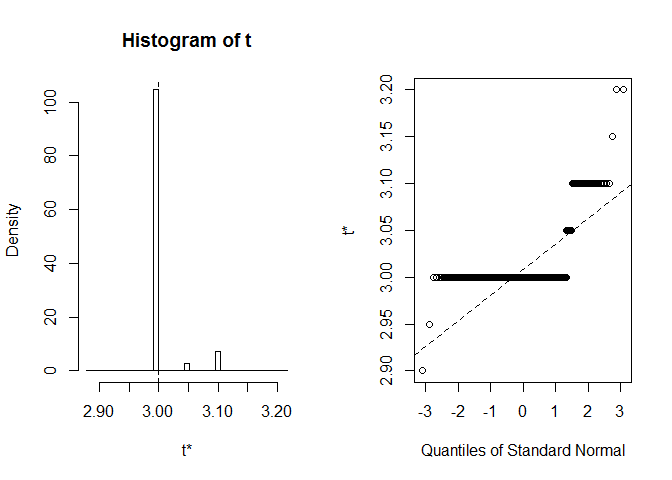
Dystrybucja realizacji bootstrap jest nietypowa. Zdecydowana większość z nich (ponad 90%) to 3.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2replikacja wyników
czasami musimy odtworzyć replikacje bootstrap. Jeśli możemy użyć R do tego, nie jest to problem. set.seed funkcja rozwiązuje problem .Odtworzenie replikacji bootstrap w innym oprogramowaniu byłoby znacznie bardziej skomplikowane. Co więcej, dla dużych R, przeliczanie w R nie może być opcją (na przykład z powodu braku czasu).
możemy sobie z tym problemem poradzić, zapisując indeksy elementów oryginalnegoaldataset, które tworzyły każdą próbkę bootstrap. Tak działa funkcja boot.array(z argumentem indices=T).
tableOfIndices<-boot.array(myBootstrap, indices=T)każdy wiersz to jedna próbka bootstrap. Np., nasz pierwszy przykład zawiera następujące elementy:
ustawienie indices=F (domyślne), otrzymamy odpowiedź na pytanie ” Ile razy każdy element oryginalnego zestawu danych pojawił się w każdym bootstrapsample?”. Na przykład w pierwszej próbce: pierwszy element zestawu danych pojawił się raz, drugi element w ogóle się nie pojawił, trzeci element pojawił się raz, czwarty raz i tak dalej.
taka tabela pozwala nam odtworzyć realizację bootstrap poza R.Lub w samym R, gdy nie chcemy użyć set.seed i ponownie wykonać całą komutację.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')sprawdźmy, czy wyniki są takie same:
tak, są!
jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym w R, weź udział w kursie Machine Learning Toolbox DataCamp.