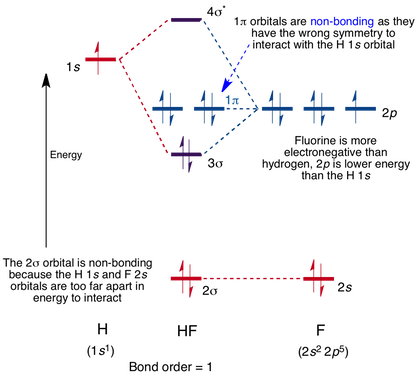
MO dla HF

orbitale molekularne dla heterogenicznych cząsteczek dwuatomowych

proste podejście do teorii orbitali molekularnych (mo) dla heterogenicznych cząsteczek dwuatomowych polega na pokazaniu diagramu poziomu energii. Poziomy energii MO można obliczyć w następujący sposób:

Przypomnijmy, że energia \(E_n\) dla liczby kwantowej n jest dla pierwiastka o atomowym Z wynosi w przybliżeniu

\

używamy \(z_{eff}\) zamiast Z, aby oznaczać, że musimy zmodyfikować liczbę atomową, aby uzyskać efektywny ładunek atomowy dla jądra. Ponieważ mamy do czynienia z wartościami przybliżonymi, można użyć Z bezpośrednio. Poziom energii orbitalnej 1s wynosi -13,6 eV dla atomów wodoru, mierzony jako energia jonizacji H.

Tak więc dla liczby kwantowej n = 1 poziom energii dla 1s He wynosi około – 54 EV. Podobnie poziom energii 1s dla F wynosi – 1101 eV. Poziom energii 2s i 2P dla He wynosi około -13,6 eV, co jest podobne do poziomu orbitalu 1s H.

zatem poziom energii 2s dla Li wynosi około -6 EV. Jednak w przypadku atomów wieloelektronowych p-subshell i S-subshell mają różne energie z powodu penetracji. Na tym poziomie nie możemy być dokładni, ale po prostu uważamy, że orbitale 2P mają wyższą energię niż orbital 2S. Zwykle orbitale atomowe o podobnych do siebie poziomach energii pokrywają się tworząc orbitale molekularne. W ten sposób dopasowujemy poziomy energetyczne orbitali atomowych, a następnie tworzymy z nich wiązania i anty-wiązania.

jednak w przypadku, gdy poziom energii orbitalnej jest bardzo różny, używamy orbitali atomowych niepełnej podpowłoki, aby utworzyć MOs.

diagram orbitalu cząsteczkowego dla cząsteczki HF

interakcja zachodzi między orbitalem 1s na wodorze a orbitalem 2P w fluorze, powodując powstanie wiązania sigma i antybondującego orbitalu cząsteczkowego sigma, jak pokazano poniżej.