Okrąg jest równomiernie podzielony na sześć równych trójkątów

Witam,

najpierw opowiem wam moje założenia jak wygląda wasze zdjęcie:

1. każdy trójkąt ma wierzchołek (róg) w środku okręgu
2. każdy trójkąt ma rogi na obwodzie okręgu (tak więc dwa boki każdego trójkąta są promieniem)
3. Trójkąty dzielą boki (nie ma przerw między trójkątami)

ogólny obraz wygląda jak kwiat – każdy trójkąt jest płatkiem.

nieznany obszar jest tym, co pozostało wokół zewnętrznej części okręgu, między obwodem a zewnętrznym bokiem każdego trójkąta. Ten nieznany obszar jest podzielony na sześć przystających sekcji (równych pod każdym względem-podobnie jak trójkąty są „równe” pod każdym względem – w tym obszar, długość boku i długość łuku). Nie jest jasne, czy masz na myśli, że pole jednego łuku jest Pi (właściwie nie dzielone, choć wymawiane tak samo), czy wszystkie sześć odcinków wziętych razem to Pi. W dalszej części, zakładam, że jedna z zewnętrznych sekcji ma pole Pi, więc pole wszystkich sześciu sekcji razem wziętych wynosi 6 razy Pi. Musimy znaleźć promień okręgu, nazwijmy go r.

użyję również P do oznaczenia Pi (lub OK. 3.14). Teraz jest wiele informacji, które możemy udekorować z trójkątów:

1. kąty w centrum wynoszą 60 stopni. Dzieje się tak dlatego, że wszystkie sześć kątów w środku jest równe, a okrąg ma 360 stopni. Tak jak 360 podzielone przez 6.
2. każdy trójkąt jest równoramienny . Dzieje się tak, ponieważ dwa boki są równe (boki, które są promieniem).
3. każdy trójkąt jest w rzeczywistości równoboczny. Ponieważ jest iscoceles, dwa zewnętrzne kąty są równe. Ale jest 180 stopni w trójkącie, 60 są już używane w kącie środkowym, pozostawiając 180-60=120 stopni dla kątów zewnętrznych. Ale 120 podzielone przez 2 to 60 stopni, więc wszystkie trzy kąty są równe, więc to jest izoskle.
4. każdy bok w każdym trójkącie ma długość r. Dzieje się tak dlatego, że mamy 6 przystających („równych” pod każdym względem) trójkątów równobocznych i ponieważ dwa boki każdego trójkąta są promieniem.

z geometrii trójkątów, musimy zrobić trochę algebry. Ponieważ znamy obszar i potrzebujemy promienia, potrzebujemy wzoru (lub równania) dla promienia w kategoriach powierzchni (w dalszej części, miej na uwadze cel wzoru). Pole okręgu TO P * r2 (r2 oznacza R do kwadratu , a * oznacza mnożenie) pole pozostałych odcinków poza trójkątami, ale wewnątrz okręgu (obszar, który już nie ma 6 * P), można również znaleźć, odejmując pole trójkątów od obszaru okręgu. Musimy znaleźć pole jednego z trójkątów równobocznych.

Metoda 1 do obliczania powierzchni trójkąta
powierzchnia trójkąta wynosi b * h/2 tutaj potrzebna jest pewna Trygonometria: narysuj linię od wierzchołka do przeciwległego boku, który dzieli przeciwległy bok na pół i jest pod kątem prostym. To dzieli trójkąt równoboczny na dwa przystające trójkąty kątowe, a nowy bok to wysokość, nazwijmy go h. musimy znaleźć h.

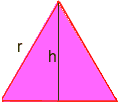
używając trygonometru w jednym z trójkątów prostokątnych, mamy sin60 = h/R, ale sin60 = SQR(3)/2, gdzie SQR(3) oznacza pierwiastek kwadratowy z trzech, więc SQR(3)/2 = h/r pomnóż obie strony przez r, aby uzyskać h = r*SQR(3)/2 R teraz pole jednego trójkąta równobocznego wynosi b*h/2 = (r)*(r*SQR(3)/2)/2 = (r2)*sqr (3)/4 r = sqr(6*P/(P-6*sqr (3)/4)) Użyj kolejności operacji do obliczenia na kalkulatorze (z P=3,14): r= 5,896… Promień okręgu wynosi ok. 5.9. Paweł