podstawy Epidemiologii
po przeczytaniu tego rozdziału będziesz mógł wykonać następujące czynności:
- wyjaśnij, czym jest modyfikacja efektu
- rozróżnij czynniki zakłócające i modyfikatory efektu
- przeprowadź analizę stratyfikowaną, aby określić, czy modyfikacja efektu jest obecna w danych
w poprzednim rozdziale omówiliśmy pomieszanie. Confounder, jak pamiętacie, jest trzecią zmienną, która jeśli nie jest odpowiednio kontrolowana, prowadzi do stronniczego oszacowania skojarzenia. Modyfikacja efektu obejmuje również trzecią zmienną (nie ekspozycję, a nie wynik) – ale w tym przypadku absolutnie nie chcemy jej kontrolować. Raczej obecność modyfikacji efektu sama w sobie jest interesującym odkryciem, a my go podkreślamy.
gdy występuje modyfikacja efektu (zwana również interakcją), będą różne wyniki dla różnych poziomów trzeciej zmiennej (zwanej również współzmienną). Na przykład, jeśli przeprowadzimy badanie kohortowe na temat ilości snu i wskaźnika GPA wśród studentów Oregon State University (OSU) w ciągu jednego semestru, możemy zebrać te dane:
| GPA | |||
| < 3.0 | ≥ 3.0 | ||
| ilość snu | < 8 godziny | 25 | 25 |
| > 8 godziny | 25 | 25 | |
ponieważ było to badanie kohortowe, obliczamy współczynnik ryzyka (RR):
nie ma związku między ilością snu a późniejszą średnią. Korzystając z szablonu zdania, można to stwierdzić:
jest to wskaźnik ryzyka z badania kohortowego, więc musimy uwzględnić ramy czasowe – co zrobiłem, mówiąc „zakończyć termin”. Podobnie jak w przypadku pomieszania, nazywamy to nieskorygowanym lub surowym RR.
jednak z rozmów ze studentami zastanawiamy się, czy płeć może być ważną zmienną. Podobnie jak w przypadku mylenia, przeprowadzilibyśmy analizę warstwową, aby sprawdzić modyfikację efektu. Ponownie, rysujemy tabele 2 × 2 z tą samą ekspozycją (sen) i wynikiem (GPA), ale rysujemy oddzielne tabele dla mężczyzn i kobiet (Płeć jest zmienna). Robimy to, patrząc wstecz na surowe dane i zastanawiając się, ilu z 25 osób w komórce A (E+, D+) powyżej było mężczyznami, a ilu kobietami. Załóżmy, że z 25 osób, które zgłosiły < 8 godzin i miały średnią < 3.0, 11 to mężczyźni, a 14 to kobiety. Następnie podobnie dzielimy uczestników z komórek B, C i D i tworzymy specyficzne dla warstwy tabele 2 x 2:
| Mężczyźni | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| ilość snu | < 8 godziny | 11 | 14 |
| 8+ godziny | 17 | 9 | |
| kobiety | GPA | ||
| < 3.0 | ≥ 3.0 | ||
| ilość snu | < 8 godziny | 14 | 11 |
| 8+ godziny | 8 | 16 | |
RRmen= \frac {(\frac{11}{25})}{(\frac{17}{26})} = 0.68
RRwomen= \frac {(\frac{14}{25})}{(\frac{8}{24})} = 1.7
interpretacje:
wśród studentów płci męskiej, ci, którzy spali mniej niż 8 godzin w nocy, mieli 0,68 razy większe ryzyko wystąpienia GPA <3.0 Na koniec okresu, w porównaniu do osób, które zgłosiły 8 lub więcej godzin.
wśród studentek, osoby, które spały mniej niż 8 godzin w nocy, miały 1,7-krotne ryzyko wystąpienia GPA <3,0 pod koniec semestru, w porównaniu do tych, które zgłosiły 8 lub więcej godzin.
Spanie poniżej 8 godzin wiąże się—w tych hipotetycznych danych-z wyższą średnią ocen wśród studentów płci męskiej („wynikiem” jest niska średnia ocen, więc RR mniejsza niż 1 wskazuje, że narażone osoby są mniej narażone na niską średnią ocen), ale z niższą średnią ocen wśród studentów płci żeńskiej.
płeć w tym przypadku działa jako modyfikator efektu: związek między snem a GPA zmienia się w zależności od warstw współzmiennych. Możesz zauważyć modyfikację efektu podczas wykonywania analizy warstwowej, biorąc pod uwagę następujące elementy:
- surowy spada między nimi
jeśli masz modyfikację efektu, następnym krokiem jest zgłoszenie środków specyficznych dla warstwy. Nie obliczamy SKORYGOWANEJ miary (byłoby blisko 1.0, podobnie jak w przypadku ropy); interesujące jest to, że mężczyźni i kobiety reagują na sen inaczej. Modyfikacja efektów jest czymś, co chcemy podkreślić w naszych wynikach, a nie czymś, co należy skorygować.
w przeciwieństwie do dezorientacji, gdzie 10% zmiana z surowego na skorygowany jest przyjętą definicją dezorientacji, nie istnieje taka standaryzowana definicja tego, jak różne muszą być środki specyficzne dla warstwy, aby nazwać coś modyfikatorem efektu. Próg powinien być prawdopodobnie wyższy niż ten niezbędny do zadeklarowania czegoś jako zakłócającego, ponieważ gdy zadeklarujesz coś jako modyfikator efektu, jesteś następnie zobowiązany do raportowania wyników oddzielnie dla każdego poziomu kowariable-czegoś, co odcina twoją moc o co najmniej połowę. Tak więc, w epidemiologii, rzadko widzimy dowody na modyfikację efektu zgłaszane w literaturze. Krótko mówiąc,” inny „wystarczy do modyfikacji efektu jest” jednoznacznie inny.”
podczas czytania artykułów modyfikacja efektów bywa nazywana interakcją lub autorzy mogą po prostu powiedzieć, że zgłaszają analizy warstwowe. Każda z tych 3 fraz jest wskazówką, że istnieje zmienna działająca jako modyfikator efektu.
efekt modyfikacji przykład II
po recesji spowodowanej bańką mieszkaniową w 2008 roku (jest to ekspozycja), gospodarka USA straciła wiele miejsc pracy. Oto wykres pokazujący liczbę ludzi, którzy pracowali (wynik) przed, w trakcie, i po recesji. Wyniki są przedstawiane warstwowo według płci (zmienna), co oznacza, że analityk podejrzewał, że płeć może działać jako modyfikator efektu. W rzeczywistości wyniki są nieco inne: mężczyźni (na niebiesko) stracili większy odsetek miejsc pracy, a od 2014 r.nie powrócili jeszcze do poziomu sprzed recesji, podczas gdy kobiety (Na Czerwono) straciły mniej miejsc pracy i do 2014 r. całkowicie wyzdrowiały.

źródło: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUs
co, jeśli również rozwarstwiamy się według wieku? Po pierwsze, oto wykres pokazujący, jak recesja wpłynęła na miejsca pracy dla osób w wieku 55 lat i starszych:
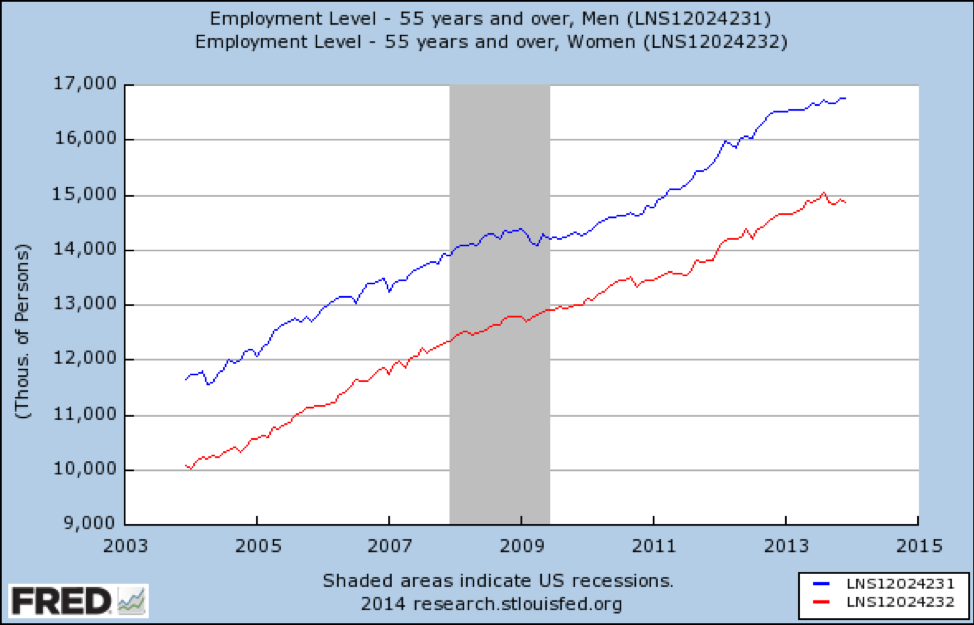
źródło: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUt
recesja w ogóle nie dotknęła starszych pracujących Amerykanów. Nie widzimy też modyfikacji efektów ze względu na płeć—dwie linie są prawie równoległe.
A co z młodymi dorosłymi?
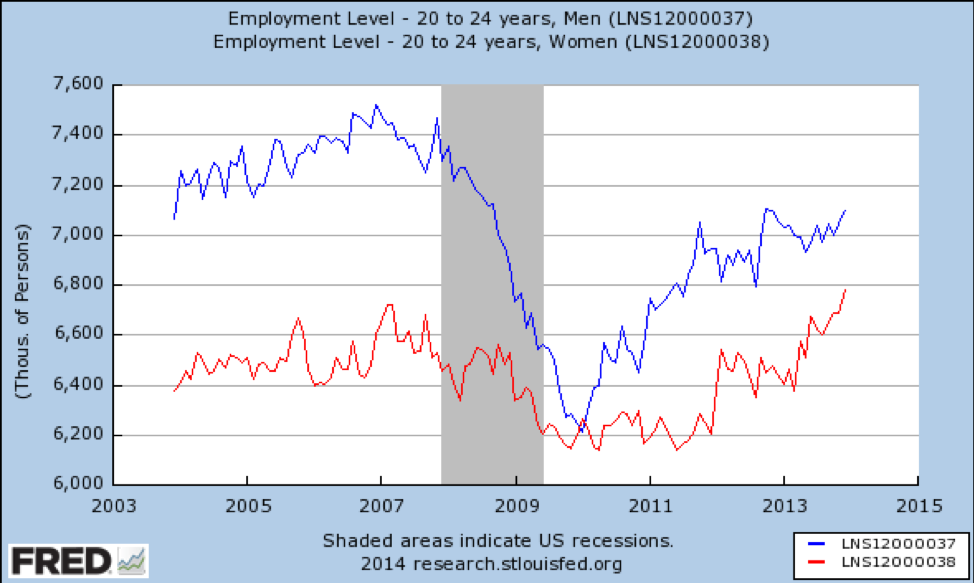
źródło: https://fred.stlouisfed.org/graph/fredgraph.png?g=qUv
Tutaj Mamy duży wpływ na zmianę płci-młodzi mężczyźni stracili ogromną część dostępnych miejsc pracy i nie wyzdrowieli w pełni od 2014 roku. Nie jest to zaskakujące, ponieważ recesja została spowodowana głównie bańką mieszkaniową, a robotnicy budowlani to głównie młodzi mężczyźni. Z kolei młode kobiety straciły niewielki odsetek miejsc pracy i szybko powróciły do poziomu lepszego niż prerecesja.
wreszcie szukamy pracy dla 25-54 latków:
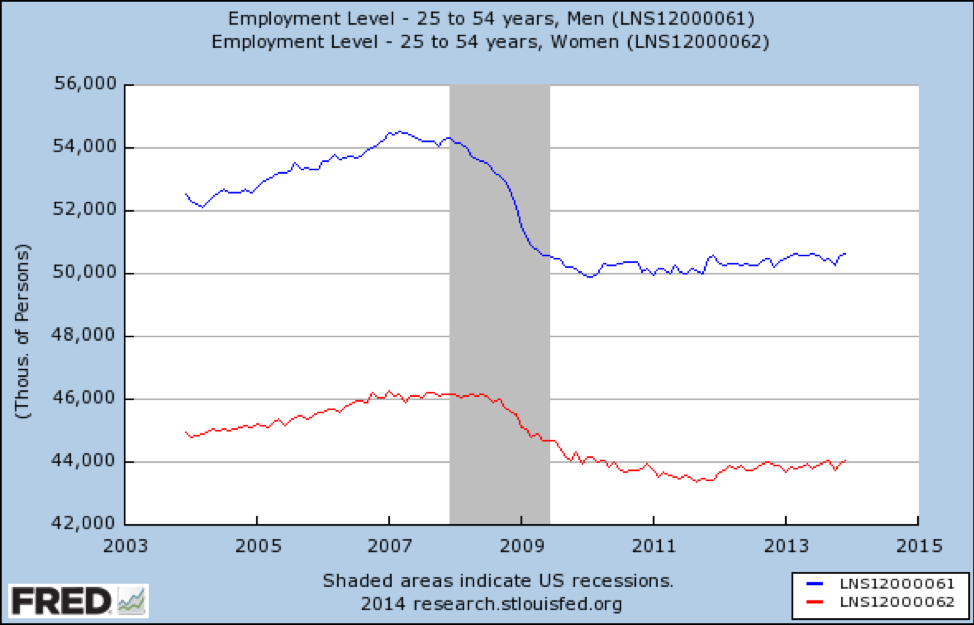
źródło: https://fred.stlouisfed.org/graph/?id=LNS12000061
tutaj widzimy bardzo ponury obraz. W tej grupie wiekowej miejsca pracy zostały utracone-więcej dla mężczyzn niż kobiet – i od 2014 r.w ogóle nie wyzdrowiały.
tak więc, analizując reakcję rynku pracy na recesję w 2008 r., widzimy znaczne zmiany w skutkach ze względu na wiek (ożywienie miejsc pracy drastycznie różniło się w zależności od wieku), a w niektórych kategoriach wiekowych również pewne dowody na zmiany w skutkach ze względu na płeć. Skutki recesji dla miejsc pracy były różne dla osób w różnym wieku i płci.
jest to ważne, ponieważ implikacje polityczne byłyby bardzo różne. Wyobraź sobie, że pracujesz jako część rządu federalnego i próbujesz zaprojektować pakiet bodźców ekonomicznych lub naprawczych. Gdyby tylko dane pochodzą z pierwszego wykresu, bez podziałów wiekowych, potencjalne rozwiązania polityczne byłyby zupełnie inne niż w przypadku uzyskania dostępu do analizy warstwowej według wieku.
z konfundowaniem, początkowo otrzymujesz złą odpowiedź, ponieważ konfunder nie jest równomiernie rozłożony między Twoje grupy. Zniekształca to miarę asocjacji, którą obliczasz (pamiętaj: większe stopy są związane z szybkością odczytu tylko z powodu mylenia według poziomu ocen). Zamiast tego musisz ponownie obliczyć miarę asocjacji, tym razem dostosowując się do confoundera.
z modyfikacją efektu, również początkowo otrzymujesz złą odpowiedź, ale tym razem jest to spowodowane tym, że Twoja próbka zawiera co najmniej 2 podgrupy, w których związek ekspozycja / choroba jest inny. W takim przypadku musisz trwale rozdzielić te podgrupy i raportować wyniki (które mogą, ale nie muszą być mylone z jeszcze innymi zmiennymi) oddzielnie dla każdej warstwy: w tym przypadku mężczyźni, którzy śpią mniej mają wyższe GPA niż mężczyźni, którzy śpią więcej, ale jednocześnie kobiety, które śpią więcej, mają wyższe GPA niż kobiety, które śpią mniej.
oto tabela podsumowująca proces radzenia sobie z potencjalnymi zakłócającymi i modyfikatorami efektów. Większość procesu jest taka sama, niezależnie od tego, jaki rodzaj współzmienności masz (we wszystkich przypadkach musisz zmierzyć współzmienność podczas badania i zmierzyć ją dobrze!). Obszary różnicy są pokazane na Czerwono.
| Konfundowanie | modyfikacja efektu | |
| przed planowaniem badania | zastanów się, jakie zmienne mogą działać jako czynniki zakłócające w oparciu o to, co wiesz o procesie narażenia/choroby w trakcie badania. | zastanów się, jakie zmienne mogą działać jako modyfikatory efektów w oparciu o to, co wiesz o badanym procesie narażenia/choroby. |
| podczas badania | zbieraj dane o potencjalnych współzmiennych – analizy stratyfikowane/skorygowane nie mogą być prowadzone bez danych na temat współzmiennych! | zbieraj dane o potencjalnych współzmiennych – analizy stratyfikowane/skorygowane nie mogą być prowadzone bez danych o współzmiennych! |
| Analiza: Krok 1 | Oblicz surową miarę asocjacji (ignorując zmienną). | Oblicz surową miarę asocjacji (ignorując zmienną). |
| Analiza: Krok 2 | Oblicz miary zależności poszczególnych warstw, tak aby każdy poziom współzmiennej miał własną tabelę 2 x 2. | Oblicz miary zależności warstwy, tak aby każdy poziom kowariable miał własną tabelę 2 x 2. |
| Analiza: Etap 3 | jeśli miary specyficzne dla warstwy są podobne do siebie i co najmniej 10% różnią się od surowca (który nie mieści się między nimi), to zmienna jest czynnikiem zakłócającym. | jeśli miary specyficzne dla warstwy są różne od siebie, a surowa leży między nimi, to zmienna jest modyfikatorem efektu. |
| pisanie wyników | zgłoś skorygowaną miarę asocjacji, która kontroluje konfundera. |
wyobraź sobie, że wykonujesz przekrojowe badanie aktywności fizycznej i demencji u osób starszych i obliczasz nieskorygowany współczynnik szans (lub) wynoszący 2,0. Uważasz, że stan cywilny może być ważną zmienną, więc rozwarstwiasz się przez „obecnie żonaty” kontra „nie obecnie żonaty” (co obejmuje nigdy nie żonaty, rozwiedziony i owdowiały). RNO wśród osób będących obecnie w związku małżeńskim wynosi 3,1, a wśród osób nie będących obecnie w związku małżeńskim RNO wynosi 3,24. W tym przypadku stan cywilny działa jako dezorientacja, a my zgłaszamy skorygowany OR (który byłby 3.18 lub tak).
wyobraź sobie, że wykonujesz randomizowane badanie diety śródziemnomorskiej, aby zapobiec przedwczesnemu porodzie u kobiet w ciąży. Wykonujesz badanie i obliczasz RR 0,90. Myślisz, że parzystość może być ważną zmienną, więc przeprowadzasz analizę warstwową. Wśród nulliparów RR wynosi 0,60, a wśród wielopar, RR wynosi 1,15. Są one różne od siebie, a surowy leży między nimi. W tym przypadku parzystość działa jako modyfikator efektu, więc należy osobno zgłosić 2 specyficzne dla warstwy RRs.
wyobraź sobie, że robisz badanie przypadków czerniaka i wcześniejszego korzystania z solarium. Surowy lub jest 3,5, ale być może płeć jest ważną zmienną. Analiza warstwowa daje wynik OR 3,45 wśród mężczyzn i 3,56 wśród kobiet. W tym przypadku zmienna (płeć) nie jest ani dezorientatorem, ani modyfikatorem efektu. Mówimy, że nie jest to confounder, ponieważ (1) surowiec leży między szacunkami specyficznymi dla warstwy 2, ale także (2) szacunki specyficzne dla warstwy nie różnią się o więcej niż 10% od surowca. Mówimy, że nie jest to modyfikator efektu, ponieważ 3,45 i 3,56 nie różnią się aż tak bardzo—w obu przypadkach efekt jest znaczący (około 3,5 razy większy). Przedstawilibyśmy prymitywne oszacowanie związku, ponieważ nie wymaga on ani dostosowania, ani stratyfikacji, aby uwzględnić skutki płci.
tak! Zwykle widzimy to, gdy zmienna o której mowa jest zmienną ciągłą, dychotomizowaną w celu sprawdzenia modyfikacji efektu. Na przykład, jeśli uważamy, że wiek może być modyfikatorem efektu, możemy podzielić naszą próbkę na ” starą „i” młodą ” do analizy stratyfikowanej—powiedzmy, starszą niż 50 kontra 50 lub młodszą. W zakresie, w jakim 51-latkowie nie są jak 70-latkowie, możemy przegapić kilka ważnych niuansów w wynikach, być może dlatego, że istnieje w danych dalsza modyfikacja efektu z większą liczbą kategorii (która spadnie do prawie zera, gdybyśmy osobno raportowali o dodatkowych warstwach) lub „szczątkowych” mylących, jak omówiono w poprzednim rozdziale. Dalsze szczegóły wykraczają poza zakres tej książki, ale wiedz, że ta sama zmienna może teoretycznie działać zarówno jako dezorientator, jak i modyfikator efektu-ale rzadko widzi się to w praktyce.
wniosek
w przeciwieństwie do confoundingu, którego efektów chcemy się pozbyć w naszej analizie, modyfikacja efektu jest interesującym odkryciem samym w sobie i my to zgłaszamy. Aby sprawdzić modyfikację efektu, przeprowadź analizę warstwową. Jeśli miary zależności warstwy są różne od siebie, a surowa leży między nimi, to jest prawdopodobne, że dana zmienna działa jako modyfikator efektu. Sprawozdanie z wyników oddzielnie dla każdej warstwy współzmiennej.
jeden finał, układaj-wszystko-razem:
| jeśli są to Twoje ORs/RRs: | ||||
| Crude / Unadjusted | Stratum | Stratum | wtedy kowariable jest … | i zgłaszasz… |
| 2.0 | 1.0 | 3.2 | modyfikator efektu | 2888 |
| 2.0 | 3.5 | 3.6 | a confounder | |
| 2.0 | 1.9 | 2.0 | nic ciekawego | surowa miara |
Błąd systematyczny w badaniu (niektórzy nazywają to stronniczością; wolę Nie), który jest spowodowany trzecią zmienną zakłócającą relację ekspozycja-choroba.
odnosi się do scenariusza, w którym zależność między ekspozycją a wynikiem zmienia się na podstawie trzeciej zmiennej. Na przykład, być może Joga zapobiega urazom ACL u kobiet, ale nie u mężczyzn. Seks w tym scenariuszu jest modyfikatorem efektu. Modyfikacja efektów nie jest tym samym, co mylenie.
prawdopodobieństwo, że Twoje badanie znajdzie coś, co tam jest. Moc = 1-β; beta jest stopniem błędu typu II. Małe badania lub badania rzadkich zdarzeń są zwykle niedostatecznie zasilane.
ile dzieci miała kobieta. Nulliparous kobiety (aka nulliparas) nie miały jeszcze pierwszego dziecka (mogą być w ciąży, ale nie urodziły jeszcze dziecka), a parous kobiety miały co najmniej jedno poprzednie dziecko. Multiparas mieli co najmniej dwoje poprzednich dzieci; primiparas mieli jedno poprzednie dziecko.
to pierwsza ciąża kobiety.
ta kobieta miała inne dzieci.