różnica między filtrami IIR i FIR: praktyczny przewodnik projektowania
filtr cyfrowy to algorytm matematyczny, który działa na cyfrowym zbiorze danych (np. danych z czujników) w celu wyodrębnienia interesujących informacji i usunięcia wszelkich niepożądanych informacji. Zastosowania tego typu technologii obejmują usuwanie usterek z danych z czujników lub nawet usuwanie szumów na mierzonym sygnale w celu łatwiejszej analizy danych. Ale jak wybrać najlepszy rodzaj filtra cyfrowego dla naszej aplikacji? A jakie są różnice między filtrem IIR a filtrem FIR?
filtry cyfrowe dzielą się na następujące dwie kategorie:
- nieskończona odpowiedź impulsowa (IIR)
- skończona odpowiedź impulsowa (FIR)
jak sugerują nazwy, każdy typ filtra jest klasyfikowany według długości jego odpowiedzi impulsowej. Jednak przed rozpoczęciem szczegółowej analizy matematycznej rozsądnie jest ocenić różnice w wydajności i charakterystyce każdego typu filtra.
przykład
w celu zilustrowania różnic między IIR i FIR, odpowiedź częstotliwościowa FIR 14.rzędu (linia stała) i Czebyszewa 4. rzędu typu i IIR (linia przerywana) przedstawiono poniżej na rysunku 1. Zauważ, że chociaż widma wielkości mają podobny stopień tłumienia, widmo fazowe filtra IIR jest nieliniowe w pasmie przepustowym (\(\small 0\rightarrow7. 5Hz\)) i staje się bardzo nieliniowe przy częstotliwości odcięcia, \(\small f_c=7.5 Hz\). Należy również zauważyć, że FIR wymaga większej liczby współczynników (15 vs IIR 10), aby dopasować charakterystykę tłumienia IIR.
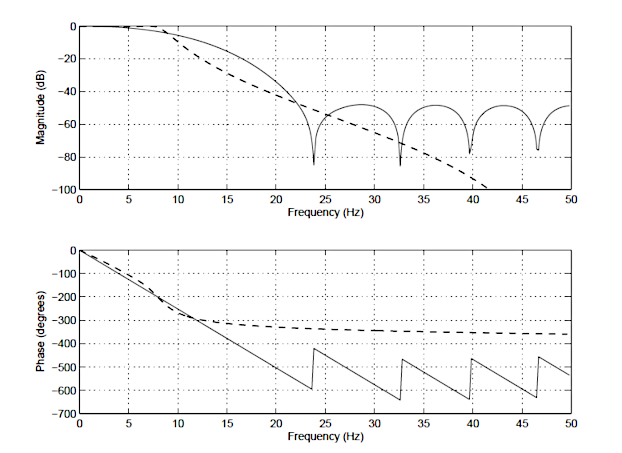
to tylko niektóre z różnic między tymi dwoma typami filtrów. Szczegółowe podsumowanie głównych zalet i wad każdego typu filtra zostanie teraz opublikowane.
filtry IIR
filtry IIR (infinite impulse response) są zazwyczaj wybierane do zastosowań, w których faza liniowa nie jest zbyt ważna, a pamięć jest ograniczona. Są one szeroko stosowane w korektach audio, biomedycznym przetwarzaniu sygnałów z czujników, inteligentnych czujnikach IoT/IIoT i szybkich aplikacjach telekomunikacyjnych/RF.
zalety
- niski koszt wdrożenia: wymaga mniej współczynników i pamięci niż filtry FIR, aby spełnić podobny zestaw specyfikacji, tj. częstotliwość odcięcia i tłumienie paska stopera.
- niskie opóźnienie: nadaje się do kontroli w czasie rzeczywistym i bardzo szybkich aplikacji RF dzięki niskiej liczbie współczynników.
- odpowiednik analogowy: może być używany do naśladowania charakterystyki filtrów analogowych za pomocą przekształceń mapowania płaszczyzn s-Z.
- charakterystyka nieliniowa fazy: Charakterystyki fazowe filtra IIR są na ogół nieliniowe, zwłaszcza w pobliżu częstotliwości odcięcia. W celu poprawy charakterystyki fazy przepustowej można stosować filtry wyrównawcze całoprzepustowe.
- bardziej szczegółowa analiza: wymaga większej analizy skalowania i przepełnienia liczbowego, gdy jest zaimplementowana w stałym punkcie. Struktura filtra Direct form II jest szczególnie wrażliwa na efekty kwantyzacji i wymaga szczególnej ostrożności na etapie projektowania.
- stabilność liczbowa: Mniej stabilne numerycznie niż ich odpowiedniki FIR (finite impulse response), ze względu na ścieżki sprzężenia zwrotnego.
filtry FIR
filtry FIR (finite impulse response) są zazwyczaj wybierane do zastosowań, w których ważna jest faza liniowa, a dostępna jest przyzwoita ilość pamięci i wydajność obliczeniowa. Mają one szeroko stosowane w zastosowaniach wzmacniających sygnał audio i Biomedyczny. Ich zerowa struktura (omówiona poniżej) zapewnia, że nigdy nie staną się niestabilne dla żadnego rodzaju sygnału wejściowego, co daje im wyraźną przewagę nad IIR.
zalety
- Faza liniowa: pierwsze mogą być łatwo zaprojektowane tak, aby miały fazę liniową. Oznacza to, że do filtrowanego sygnału nie wprowadza się zniekształceń fazowych, ponieważ wszystkie częstotliwości są przesunięte w czasie o tę samą ilość – zachowując w ten sposób relatywne relacje harmoniczne (tj. stałe opóźnienie grupowe i fazowe). Z pewnością nie ma to miejsca w przypadku filtrów IIR, które mają nieliniową charakterystykę fazową.
- stabilność: jako pierwsi nie używają poprzednich wartości wyjściowych do obliczenia ich obecnego wyjścia, np. nie mają sprzężenia zwrotnego, nigdy nie mogą stać się niestabilne dla żadnego rodzaju sygnału wejściowego, co daje im wyraźną przewagę nad filtrami IIR.
- Dowolna odpowiedź częstotliwościowa: funkcja Firarb() Parks-McClellan i ASN FilterScript pozwalają na zaprojektowanie FIR o dowolnej wielkości odpowiedzi. Oznacza to, że jodła może być dostosowywana łatwiej niż IIR.
- wydajność punktu stałego: efekty kwantyzacji są mniej dotkliwe niż efekty IIR.
- wysokie wymagania obliczeniowe i pamięci: Jodły zwykle wymagają o wiele więcej współczynników do osiągnięcia ostrego odcięcia niż ich odpowiedniki IIR. Konsekwencją tego jest to, że wymagają znacznie więcej pamięci i znacznie większej ilości operacji MAC (wielokrotnych i akumulacyjnych). Jednak nowoczesne architektury mikrokontrolerów oparte na rdzeniach Cortex-M Arm zawierają teraz obsługę sprzętową DSP za pośrednictwem SIMD (signal instruction, multiple data), które znacznie przyspieszają operację filtrowania.
- wyższe opóźnienie: wyższa liczba współczynników oznacza, że ogólnie FIR jest mniej odpowiedni niż IIR do szybkich zastosowań o dużej przepustowości. Staje się to problematyczne w zastosowaniach sterowania zamkniętą pętlą w czasie rzeczywistym, gdzie filtr FIR może mieć zbyt duże opóźnienie grupowe, aby osiągnąć stabilność pętli.
- brak analogowego odpowiednika: wykorzystując Dwuliniową, dopasowaną transformatę z (mapowanie s-z), filtr analogowy można łatwo przekształcić w równoważny filtr IIR. Jednak nie jest to możliwe dla FIR, ponieważ nie ma analogowego odpowiednika.
definicje Matematyczne
jak omówiono we wstępie, nazwa IIR i FIR pochodzą od matematycznych definicji każdego typu filtra, tj. filtr IIR jest klasyfikowany przez jego teoretycznie nieskończoną odpowiedź impulsową,
y (n)= \ sum_{k = 0}^{\infty}h (k) x (n-k)
\)
i FIR skategoryzowany przez jego skończoną odpowiedź impulsową,
y (n)= \ sum_{k = 0}^{N-1} h (k) x (n-k)
\)
następnie przeanalizujemy właściwości matematyczne każdego typu filtra.
definicja IIR
jak widać powyżej, filtr IIR jest klasyfikowany według jego teoretycznie nieskończonej odpowiedzi impulsowej,
\(\displaystyle y (n)=\sum_{K=0}^{\infty}h(k) x(n-k)\)
praktycznie rzecz biorąc, nie jest możliwe obliczenie wyniku IIR za pomocą tego równania. W związku z tym równanie można zapisać ponownie w postaci skończonej liczby biegunów \(\small p\) i zer \(\small q\), zgodnie z równaniem liniowej różnicy współczynników stałych, określonym przez:
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p} a_ky (n-k)
\)
gdzie, \(\small a_k\) i \(\small b_k\) są mianownikiem i licznikiem wielomianów filtra, którego pierwiastki są równe biegunom filtra i zerom odpowiednio. Tak więc zależność między równaniem różnicy a z-transformatą (funkcją przeniesienia) można zdefiniować za pomocą własności opóźnienia z-transformaty takiej, że,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}} {1+ \ sum \ limits_{K=1}^p a_kz^{- k}}
\)
jak widać, funkcja transferu jest reprezentacją domeny częstotliwości filtra. Zauważ również, że bieguny działają na danych wyjściowych, a zera na danych wejściowych. Ponieważ bieguny działają na dane wyjściowe i wpływają na stabilność, istotne jest, aby ich promienie pozostały wewnątrz okręgu jednostkowego (tj. <1) dla stabilności BIBO (bounded input, bounded output). Promienie zer są mniej krytyczne, ponieważ nie wpływają na stabilność filtra. Jest to główny powód, dla którego wszystkie zerowe filtry FIR (finite impulse response) są zawsze stabilne.
stabilność BIBO
system liniowej niezmienności czasu (LTI) (taki jak filtr cyfrowy) jest uważany za bounded input, bounded output stable lub Bibo stable, jeśli każde ograniczone wejście powoduje powstanie bounded output, jako
\(\displaystyle \sum_{K=0}^{\infty}\left|h(k)\right|<\infty \)
gdzie, \(\small h(k)\) jest odpowiedzią impulsową układu LTI. Analizując to równanie, powinno być jasne, że kryterium stabilności BIBO będzie spełnione tylko wtedy, gdy bieguny systemu leżą wewnątrz okręgu jednostkowego, ponieważ ROC systemu (region konwergencji) musi obejmować okrąg jednostkowy. W związku z tym wystarczy powiedzieć, że Ograniczony sygnał wejściowy zawsze wytworzy Ograniczony sygnał wyjściowy, jeśli wszystkie bieguny leżą wewnątrz okręgu jednostkowego.
zera z drugiej strony nie są ograniczone tym wymogiem i w konsekwencji mogą leżeć w dowolnym miejscu na płaszczyźnie z, ponieważ nie wpływają bezpośrednio na stabilność systemu. W związku z tym, analiza stabilności systemu może być przeprowadzona przez najpierw obliczenie pierwiastków funkcji przeniesienia (tj. pierwiastków wielomianów licznika i mianownika), a następnie wykreślenie odpowiednich biegunów i zer na płaszczyźnie Z.
ciekawa sytuacja pojawia się, gdy bieguny leżą na okręgu jednostkowym, ponieważ mówi się, że układ jest marginalnie stabilny, ponieważ nie jest ani stabilny, ani niestabilny. Chociaż układy marginalnie stabilne nie są stabilne BIBO, zostały one wykorzystane przez projektantów oscylatorów cyfrowych, ponieważ ich odpowiedź impulsowa zapewnia prostą metodę generowania fal sinusoidalnych, która okazała się nieoceniona w dziedzinie telekomunikacji.
filtry Biquad IIR
opisywana tutaj implementacja filtra IIR to biquad, ponieważ ma dwa bieguny i dwa zera, jak pokazano poniżej na rysunku 2. Implementacja biquad jest szczególnie przydatna w przypadku implementacji stałych punktów, ponieważ efekty kwantyzacji i stabilności numerycznej są zminimalizowane. Jednak ogólny sukces każdej implementacji biquad zależy od dostępnej precyzji liczb, która musi być wystarczająco wystarczająca, aby zapewnić, że kwantyzowane bieguny zawsze znajdują się wewnątrz okręgu jednostkowego.
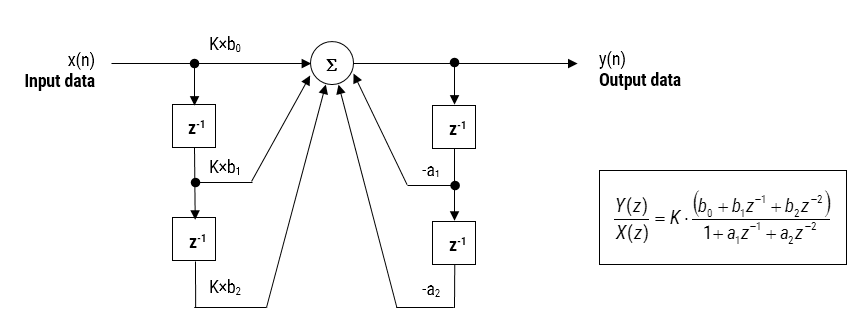
Rysunek 2: bezpośrednia forma i (biquad) realizacja filtra IIR i funkcja transferu.
analizując Rysunek 2, można zauważyć, że struktura biquad składa się z dwóch ścieżek sprzężenia zwrotnego (skalowanych przez \(\small a_1\) i \(\small a_2\)), trzech ścieżek przekazywania danych (skalowanych przez \(\small b_0, b_1\) i \(\small b_2\)) oraz wzmocnienia sekcji, \(\small K\). Tak więc operację filtrowania na rysunku 1 można podsumować następującym prostym równaniem rekurencyjnym:
\(\displaystyle y(n)=K\times\Big – a_1 y(n-1) – a_2 y (n-2)\)
analizując równanie, zauważ, że implementacja biquad wymaga tylko czterech dodatków (wymaga tylko jednego akumulatora) i pięciu mnożenia, które można łatwo umieścić na dowolnym mikrokontrolerze Cortex-M. Wzmocnienie sekcji, \(\small K\) może być również wstępnie pomnożone przez współczynniki ścieżki do przodu przed implementacją.
zbiór filtrów Biquad jest określany jako Kaskada Biquad, jak pokazano poniżej.

ASN Filter Designer może zaprojektować i wdrożyć kaskadę do 50 biquadów (tylko w wersji Professional).
implementacja zmiennoprzecinkowa
podczas implementacji filtra w zmiennej zmiennoprzecinkowej (tj. przy użyciu arytmetyki podwójnej lub pojedynczej precyzji) struktury Direct Form II są uważane za lepszy wybór niż struktura Direct Form I. Struktura transponowana Formula_2 jest uważana za najbardziej dokładną numerycznie dla implementacji zmiennoprzecinkowej, ponieważ niepożądane skutki swampingu numerycznego są zminimalizowane, co widać analizując Równania różniczkowe.
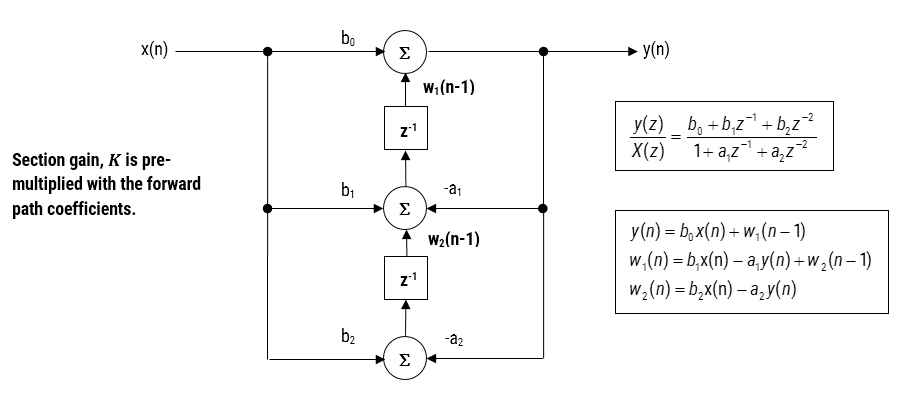
Rysunek 3-formularz bezpośredni II transponowane strucutre, funkcja transferu i równania różnicy
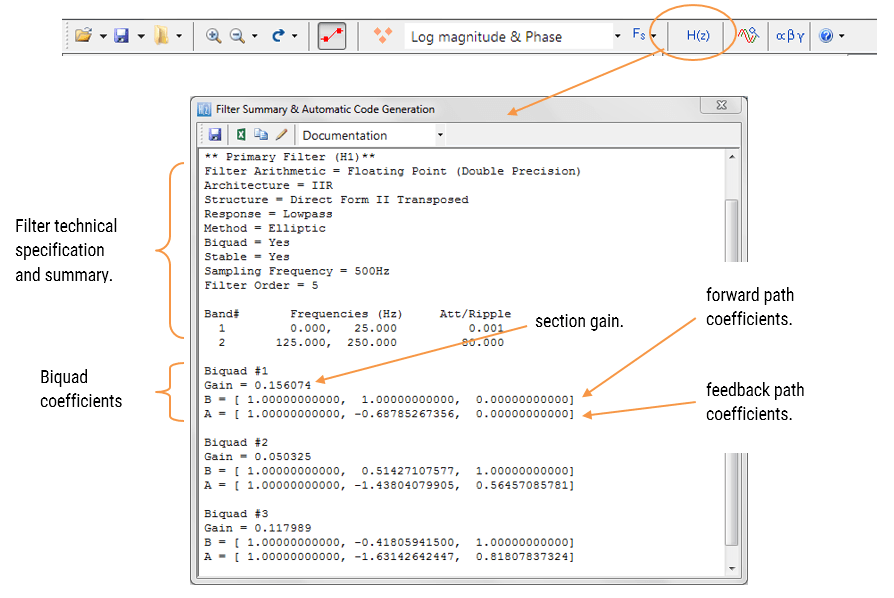
podsumowanie filtra (pokazane na rysunku 4) zapewnia projektantowi szczegółowy przegląd zaprojektowanego filtra, w tym szczegółowe podsumowanie specyfikacji technicznych i współczynników filtra, co przedstawia szybką i prostą drogę do udokumentowania projektu.
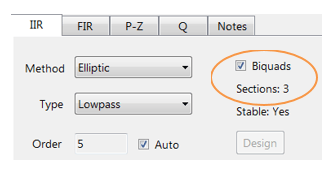
ASN Filter Designer wspiera projektowanie i implementację filtrów IIR zarówno pojedynczych sekcji, jak i Biquad (ustawienie domyślne).
definicja FIR
zwracanie równania liniowej różnicy współczynników stałych IIR, tj.
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{K=1}^{p} a_ky (n-k)
\)
zauważ, że gdy ustawimy współczynniki \(\small a_k\) (tj. sprzężenie zwrotne) na zero, definicja zmniejsza się do naszej pierwotnej definicji filtra FIR, co oznacza, że obliczenia FIR są oparte tylko na przeszłych i obecnych wartościach wejściowych, a mianowicie:
y(n)=\sum_{k=0}^{q}b_kx (n-k)
\)
implementacja
chociaż istnieje kilka praktycznych implementacji dla pierwszych, struktura formy bezpośredniej i jej transponowany kuzyn są prawdopodobnie najczęściej używane,i jako takie, wszystkie zaprojektowane współczynniki filtra są przeznaczone do implementacji w strukturze formy bezpośredniej.
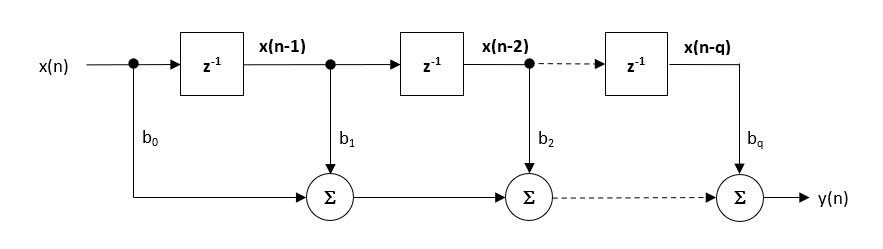
poniżej przedstawiono strukturę postaci bezpośredniej i związane z nią równanie różnicy. Forma bezpośrednia jest zalecana do realizacji stałych punktów dzięki koncepcji pojedynczego akumulatora.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx (n-q) \)
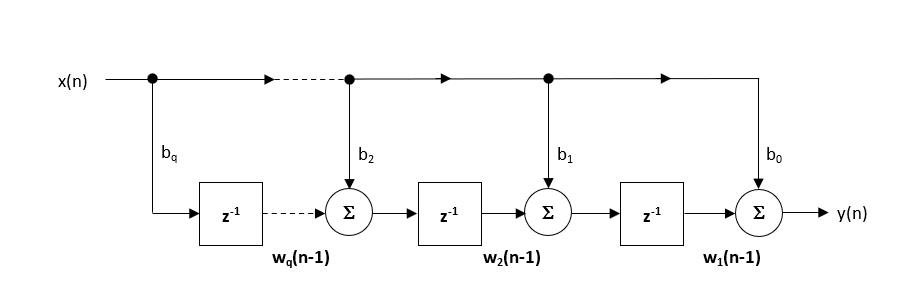
zalecana (domyślna) struktura w ASN Filter Designer jest strukturą transponowaną przez Direct Form, ponieważ zapewnia doskonałą dokładność numeryczną przy użyciu arytmetyki zmiennoprzecinkowej. Można to łatwo zauważyć, analizując równania różnicowe poniżej (używane do implementacji), ponieważ niepożądane skutki swampingu numerycznego są zminimalizowane, ponieważ dodawanie zmiennoprzecinkowe jest wykonywane na liczbach o podobnej wielkości.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(N) &+& w_3(N-1) \\ \vdots\quad &=& \Quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
czego się nauczyliśmy?
filtry cyfrowe są podzielone na następujące dwie kategorie:
- nieskończona odpowiedź impulsowa (IIR)
- skończona odpowiedź impulsowa (FIR)
filtry IIR (infinite impulse response) są zazwyczaj wybierane do zastosowań, w których faza liniowa nie jest zbyt ważna, a pamięć jest ograniczona. Są one szeroko stosowane w korektach audio, biomedycznym przetwarzaniu sygnałów z czujników, inteligentnych czujnikach IoT/IIoT i szybkich aplikacjach telekomunikacyjnych/RF.
filtry FIR (finite impulse response) są zazwyczaj wybierane do zastosowań, w których ważna jest faza liniowa i dostępna jest przyzwoita ilość pamięci i wydajność obliczeniowa. Mają one szeroko stosowane w zastosowaniach wzmacniających sygnał audio i Biomedyczny.
ASN Filter Designer zapewnia inżynierom wszystko, czego potrzebują do projektowania, eksperymentowania i wdrażania złożonych filtrów cyfrowych IIR i FIR do różnych zastosowań pomiarowych czujników. Te zalety w połączeniu z funkcją automatycznego generowania dokumentacji i kodu pozwalają inżynierom zaprojektować i zweryfikować filtr cyfrowy IIR / FIR w ciągu kilku minut, a nie godzin.
