używanie logarytmów w świecie rzeczywistym
Logarytmy są wszędzie. Używałeś kiedyś następujących zwrotów?
- 6 liczby
- dwucyfrowe
- rząd wielkości
- stopa procentowa
opisujesz liczby w kategoriach ich potęg 10, logarytmu. A stopa procentowa jest logarytmem wzrostu inwestycji.
dziwisz się, że logarytmy są tak powszechne? Ja też. Większość prób matematyki w świecie rzeczywistym (TM) wskazuje logarytmy w jakimś tajemnym wzorze lub udaje, że jesteśmy geologami zafascynowanymi skalą Richtera. „Naukowcy dbają o dzienniki, i Ty też powinieneś. Ponadto, czy możesz wyobrazić sobie świat bez cynku?”
Nie, Nie, Nie, Nie, Nie, Nie! (Mama mia!)
Matematyka wyraża pojęcia z notacją taką jak ” ln ” lub „log”. Znalezienie „matematyki w realnym świecie”oznacza napotkanie pomysłów w życiu i zobaczenie, jak można je zapisać z zapisem. Nie szukaj dosłownych symboli! Kiedy ostatni raz napisałeś znak dywizji? Kiedy ostatnio posiekałeś trochę jedzenia?
Ok, OK, rozumiemy: o czym są logarytmy?
Logarytmy znajdują przyczynę efektu, tj. wejście dla jakiegoś wyjścia
częstym „efektem” jest obserwowanie wzrostu czegoś, jak przejście z \$100 do \$150 W ciągu 5 lat. Jak to się stało? Nie jesteśmy pewni, ale logarytm znajduje możliwą przyczynę: ciągły powrót LN(150/100) / 5 = 8.1% uwzględniłby tę zmianę. To może nie być faktyczna przyczyna (czy cały wzrost nastąpił w ostatnim roku?), ale jest to gładka średnia, którą możemy porównać do innych zmian.
nawiasem mówiąc, pojęcie „przyczyny i skutku” jest niuansowe. Dlaczego 1000 jest większe niż 100?
- 100 jest 10, które rosły same przez 2 okresy czasu($10 * 10$)
- 1000 jest 10, które rosły same przez 3 okresy czasu($10 * 10 * 10$)
możemy myśleć o liczbach jako wyjściach (1000 to „1000 wyjść”) i wejściach („ile razy 10 musi rosnąć, aby uzyskać te wyjścia?”). Więc,
1000 outputs > 100 outputsponieważ
3 inputs > 2 inputslub innymi słowy:
log(1000) > log(100)dlaczego jest to przydatne?
Logarytmy umieszczają liczby w skali przyjaznej człowiekowi.
Wielkie liczby łamią nam mózgi. Miliony i biliony są „naprawdę duże”, mimo że milion sekund to 12 dni, a bilion sekund to 30 000 lat. To różnica między amerykańskim rokiem wakacji a całą ludzką cywilizacją.
trikiem do pokonania „ogromnej ślepoty liczbowej” jest zapisywanie liczb w kategoriach „wejść” (tj. ich baza mocy 10). Ta mniejsza skala (od 0 do 100) jest znacznie łatwiejsza do uchwycenia:
- moc 0 = $10^0$ = 1 (pojedynczy element)
- moc 1 = $10^1$ = 10
- moc 3 = $10^3$ = tysiąc
- moc 6 = $10^6$ = milion
- moc 9 = $10^9$ = miliard
- moc 12 = $10^12$ = bilion
- moc 23 = $10^23$ = liczba cząsteczek w kilkunastu gramach węgla
- moc 80 = $10^80$ = liczba cząsteczek we wszechświecie
skala od 0 do 80 doprowadziła nas od pojedynczego elementu do liczby rzeczy we wszechświecie. Nie za bardzo.
Logarytmy liczą mnożenie jako kroki
Logarytmy opisują zmiany w zakresie mnożenia: w powyższych przykładach każdy krok jest 10x większy. Z logarytmem naturalnym każdy krok to” e ” (2,71828…) razy więcej.
kiedy mamy do czynienia z serią mnożenia, logarytmy pomagają je „policzyć”, tak jak dla nas liczy się dodawanie, gdy dodawane są efekty.
Pokaż mi matematykę
czas na mięso: zobaczmy, gdzie pojawiają się logarytmy!
pensja Sześciocyfrowa lub wydatek dwucyfrowy
liczby opisujemy w kategoriach ich cyfr, tzn. ile mają mocy 10 (są w dziesiątkach, setkach, tysiącach, dziesięciu tysiącach itp.). Dodanie cyfry oznacza „pomnożenie przez 10”, tzn.
![]()
Logarytmy liczą liczbę dodanych mnożeń, więc zaczynając od 1 (pojedynczej cyfry) dodajemy jeszcze 5 cyfr ($10^5$) i 100 000 otrzymuje wynik 6-cyfrowy. Mówienie o” 6 „zamiast” sto tysięcy ” jest istotą logarytmów. Daje szorstkie poczucie skali bez wchodzenia w szczegóły.
pytanie bonusowe: jak opisałbyś 500 000? Powiedzenie „6 cyfra” jest mylące, ponieważ 6-cyfry często implikuje coś bliżej 100,000. Czy” 6,5 cyfry ” zadziała?
nie bardzo. W naszych głowach, 6.5 oznacza „w połowie” między 6 a 7 cyframi, ale to sposób myślenia żmija. Z logarytmami a”.5 ” oznacza połowę pod względem mnożenia, tj. pierwiastek kwadratowy ($9^.5$ oznacza pierwiastek kwadratowy z 9 — 3 jest w połowie pod względem mnożenia, ponieważ jest to 1 do 3 i 3 do 9).
biorąc log(500 000) otrzymujemy 5.7, dodajemy 1 dla dodatkowej cyfry i możemy powiedzieć ” 500 000 to 6.7 cyfr”. Spróbuj tutaj:
rząd wielkości
my maniacy uwielbiamy to wyrażenie. Oznacza to mniej więcej „10-krotną różnicę”, ale po prostu brzmi chłodniej niż”1 cyfra większa”.
w komputerach, gdzie wszystko jest liczone bitami (1 lub 0), każdy bit ma efekt podwojenia (nie 10x). Więc przejście od 8 do 16 bitów to „8 rzędów wielkości” czyli $2^8 = 256$ razy większe. („Większy” w tym przypadku odnosi się do ilości pamięci, którą można zaadresować.) Przejście od 16 do 32 bitów oznacza dodatkowe 16 rzędów wielkości, czyli $ 2^16 $ ~ 65,536 razy więcej pamięci, którą można zaadresować.
stopy procentowe
Jak obliczyć stopy wzrostu? Kraj nie zamierza rosnąć na poziomie 8,56% rocznie. Patrzymy na PKB w jednym roku, a w drugim na PKB i bierzemy logarytm, by znaleźć ukrytą stopę wzrostu.
moje dwie ulubione interpretacje logarytmu naturalnego (LN (x)), czyli logarytmu naturalnego z 1.5:
- zakładając 100% wzrost, jak długo trzeba rosnąć, aby dostać się do 1.5? (.405, mniej niż połowa czasu)
- zakładając 1 jednostkę czasu, jak szybko trzeba urosnąć, aby dostać się do 1,5? (40.5% rocznie, stale powiększane)
dzięki Logarytmom wiemy, jak szybko się rozwijamy.
skala pomiaru: Google PageRank
Google daje każdej stronie w Internecie wynik (PageRank), który jest przybliżoną miarą autorytetu / znaczenia. Jest to skala logarytmiczna, która w mojej głowie oznacza „PageRank liczy liczbę cyfr w Twoim wyniku”.
tak więc strona z pagerank 2 („2 cyfry”) jest 10x bardziej popularna niż strona z PageRank 1. Moja strona ma PageRank 5, a CNN ma PageRank 9, więc jest różnica 4 rzędów wielkości ($10^4$ = 10,000).
z grubsza mówiąc, mam około 7000 wizyt dziennie. Korzystając z mojej matematyki koperty, mogę zgadnąć CNN dostaje około 7000 * 10,000 = 70 milionów wizyt / dzień. (Jak to zrobiłem? W mojej głowie wydaje mi się, że $7k * 10k = 70 * k * k = 70 * m$). Mogą mieć kilka razy więcej niż to (100M, 200M), ale prawdopodobnie nie do 700M.
Google przekazuje wiele informacji w bardzo szorstkiej skali (1-10).
skala pomiaru: Richter, Decybel itp.
westchnienie Mamy typowy przykład „logarytmów w świecie rzeczywistym”: Skala Richtera i Decybel. Chodzi o to, aby umieścić zdarzenia, które mogą się drastycznie różnić (trzęsienia ziemi) w jednej skali z małym zakresem (zwykle 1 do 10). Podobnie jak PageRank, każdy wzrost o 1 punkt to 10-krotne zwiększenie mocy. Największe trzęsienie ziemi odnotowane przez człowieka miało 9,5; wpływ na Półwysep Jukatan, który prawdopodobnie spowodował wyginięcie dinozaurów, wynosił 13.
decybele są podobne, choć mogą być ujemne. Dźwięki mogą przejść od intensywnie cichego (pindrop) do niezwykle głośnego (samolot), a nasz mózg może to wszystko przetworzyć. W rzeczywistości dźwięk silnika samolotu jest miliony (miliardy, biliony) razy silniejszy niż pindrop, i niewygodne jest mieć skalę, która sięga od 1 do gazillion. Dzienniki utrzymują wszystko w rozsądnej skali.
wykresy logarytmiczne
często zobaczysz elementy wykreślone na „skali loga”. W mojej głowie oznacza to, że jedna strona liczy „liczbę cyfr” lub „liczbę mnożenia”, a nie samą wartość. Ponownie, pomaga to pokazać szalenie różne wydarzenia w jednej skali (od 1 do 10, a nie od 1 do miliardów).
prawo Moore ’ a to świetny przykład: co 18 miesięcy podwajamy liczbę tranzystorów(Zdjęcie dzięki uprzejmości Wikipedia).
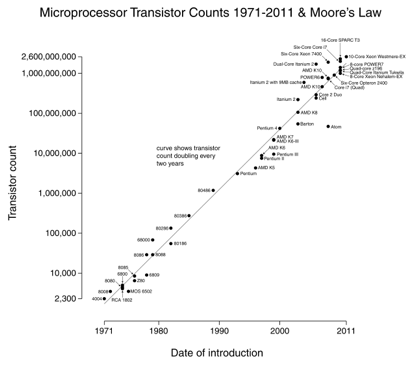
schludną rzeczą w wykresach skali logów są wykładnicze zmiany (prędkość procesora) pojawiające się jako linia prosta. Rosnące 10x rocznie oznacza, że stale maszerujesz w górę skali „cyfr”.
jeśli koncepcja jest dobrze znana, ale nie lubiana, oznacza to, że musimy zbudować naszą intuicję. Znajdź analogie, które działają, i nie zadowalaj się popaprańcami, które podręcznik wydłuży. In My head:
- Logarytmy znajdują główną przyczynę efektu (patrz wzrost, znajdź stopę procentową)
- pomagają liczyć mnożenia lub cyfry, z premią częściowych liczeń (500k to 6,7-cyfrowa liczba)
szczęśliwej matematyki.
inne posty z tej serii
- intuicyjny przewodnik po funkcjach wykładniczych & e
- Demystyfikacja logarytmu naturalnego (Ln)
- wizualny przewodnik po prostych, złożonych i ciągłych stopach procentowych
- wspólne definicje e (pokolorowane)
- rozumienie wykładników (dlaczego 0^0 = 1?)
- używanie logarytmów w świecie rzeczywistym
- jak myśleć z wykładnikami i Logarytmami
- zrozumienie dyskretnego vs. ciągłego wzrostu
- co tak naprawdę oznacza wykładnik?
- P: Dlaczego e jest wyjątkowy? (2.718… nie 2, 3.7 czy inna liczba?)