Układ słoneczny: Ziemia i Księżyc
planety są daleko od nas dziesiątki do setek milionów kilometrów. Aby uniknąć użycia tak dużych liczb, jako jednostkę odległości przyjmuje się jednostkę astronomiczną (UA), czyli średnią odległość między Ziemią a Słońcem, 149 600 000 km.światło zajmuje 8 minut i 19 sekund, aby pokryć tę odległość.
Rozmiar układu słonecznego przekracza orbitę Plutona znajdującą się na 40 Au i jest zdefiniowany jako taki, w którym siła przyciągania słońca jest równa sile przyciągania najbliższych nam gwiazd. Wtedy wymiary Układu Słonecznego będą rzędu 1, 5 105 AU oczywiste jest, że wymiary te są bardzo małe w porównaniu do wielkości galaktyki lub widzialnego wszechświata. Jednostki miary, które są akceptowane do pomiaru tych ogromnych odległości , to rok świetlny i parsec wynoszący 206 265 Au lub 3, 26 lat świetlnych.
planety Układu Słonecznego dzielą się na dwie grupy: grupę ziemską złożoną z Merkurego, Wenus, ziemi i Marsa oraz grupę gigantycznych planet składających się z Jowisza, Saturna, Urana i Neptuna.
wszystkie planety oprócz Wenus i Merkurego mają satelity, z których większość należy do Planet olbrzymich. Ziemia, Jowisz, Saturn i Neptun mają największe księżyce: Księżyc, księżyce Jowisza odkryte przez Galileusza (Io, Europa, Ganymede, Callisto), satelitę Saturna Tytana i Neptuna Trytona.
planetoidy zajmują rozległy, pierścieniowy obszar położony między orbitami Marsa i Jowisza, w średniej odległości 2, 75 Au od Słońca. Największą planetoidą jest Ceres o średnicy 1000 km.
komety skatalogowane około 600 dzielą się na dwie grupy: krótki okres (do 20 lat) i długi okres (powyżej 20 lat). Istnieją różne hipotezy dotyczące pochodzenia komet, w tym Holenderski astronom J. Lo.
oprócz nazwanych ciał w przestrzeni międzyplanetarnej istnieje duża liczba cząstek o różnych rozmiarach, dominują cząstki o masie tysięcznej lub milionowej grama, zwane pyłem meteorowym. Powstawanie tych cząstek jest prawdopodobnie spowodowane zderzeniem większych ciał (asteroid) i ich sekwencyjną fragmentacją przez całe istnienie i ewolucję Układu Słonecznego.
pył meteorów jest spowodowany zjawiskiem światła zodiakalnego, które obserwuje się po zmroku lub przed świtem, z powodu rozproszenia światła przez te cząsteczki pyłu. Większość cząstek odparowuje po wejściu do atmosfery ziemskiej (na wysokościach od 80 do 120 KM), tylko niewielka część dociera do powierzchni Ziemi.
Spójrzmy teraz na niektóre dane dotyczące planet Układu Słonecznego,
pierwszy słońca
| ciało niebieskie | Radio | Masa |
|---|---|---|
| Słońce | 6.96 * 108 m | 1.98 * 1030 kg |
potem na Ziemi
| ciało niebieskie | półoś większa | okres | Masa |
|---|---|---|---|
| Ziemia | 149.6 * 109 m | 1 rok=365.26 dni | 5.98·1024 kg |
i inne planety
| Planeta | Półoś powyżej (UA) | Mimośród | Okresu (lata) | Masa |
|---|---|---|---|---|
| Rtęć | 0.387 | 0.206 | 0.24 | 0.06 |
| Wenus | 0.723 | 0.007 | 0.62 | 0.82 |
| Ziemia | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jowisz | 5.203 | 0.048 | 11.86 | 318 |
| Saturn | 9.539 | 0.056 | 29.46 | 95.1 |
| Uran | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptun | 30.058 | 0.009 | 164.8 | 17.2 |
W poniższej tabeli przedstawiono dane dodatkowe:
- nachylenie płaszczyzny orbity planety względem ekliptyki (płaszczyzny orbity Ziemi)
- okres obrotu wokół własnej osi. Bardzo trudno było zmierzyć tę wielkość dla planet takich jak Merkury i Wenus. Gazowe skorupy Jowisza, Saturna, Urana i Neptuna mają właściwość rotacji różnicowej, to znaczy ich okresy rotacji różnią się w zależności od szerokości geograficznej.
- nachylenie osi obrotu względem płaszczyzny orbity. W przypadku Wenus jest to 177º, co odpowiada temu, że nachylenie osi wynosi 3º, ale kierunek obrotu jest odwrotny. Ten sam argument dotyczy Urana, co wskazuje, że oś obrotu Urana znajduje się prawie w płaszczyźnie jego orbity.
| Planeta | nachylenie orbity | okres obrotu | gęstość, g/cm3 | Promień równikowy (km) | nachylenie osi | liczba satelitów |
|---|---|---|---|---|---|---|
| rtęć | 7.0 | 58d.6 | 5.44 | 2 439 | <30 | 0 |
| Wenus | 3.4 | 243d | 5.24 | 6 051 | 177 | 0 |
| Ziemia | 0 ° | 23.9 | 5.52 | 6 378 | 23.5 | 1 |
| Mars | 1.8 | 24.6 | 3.95 | 3 394 | 25.2 | 2 |
| Jowisz | 1.3 | 9h.9 | 1.33 | 71 398 | 3.1 | 16 |
| Saturn | 2.5 | 10h.2 | 0.69 | 60 000 | 26.4 | 17 |
| Uran | 0°.8 | 10h.8 | 1.26 | 25 400 | 98º | 5 |
| Neptun | 1.8 | 15h.8 | 1.67 | 24 750 | 29 | 2 |
satelity
na koniec przedstawiamy niektóre dane dotyczące głównych satelitów Planet. Jowisz i Saturn mają wiele księżyców, których rozmiar jest znacznie większy niż Mars, ale wspomnij tylko o tych, które są tego samego rozmiaru lub większe niż nasz Księżyc.
| Planeta | satelity | gęstość, g/cm3 | nośnik radiowy (km) | „Orbita radiowa” (103 km) | okres (dni) |
|---|---|---|---|---|---|
| Ziemia | Księżyc | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Fobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Demos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jowisz | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganimedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturn | Tytan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptun | Triton | 2 200 | 394.7 | 5.84 |
aktywności
- określić masę planety Jowisz na podstawie danych, radio i w okresie rewolucji jednego z jej satelitów.
- określić promień orbity satelity planety Jowisz, Z Masy tej planety i okres obrotu satelity.
- określić intensywność pola grawitacyjnego g na powierzchni planet i niektórych satelitów, na podstawie danych z jego masy M i promienia R lub jego gęstości ρ i promienia.
przykład: określ masę Jowisza, wiedząc, że promień orbity Io wynosi 421 600 km, a jego okres obrotu wynosi 1.769 dni. Dane: stałe g wartości 6.67 * 10-11 nm2/KG2
przykład: Oblicz promień orbity satelity Callisto, wiedząc, że jego okres obrotu wynosi 16.689 dni, a masa planety Jowisz wynosi 1.901·1027 kg. Dane: stałe G są warte 6.67 * 10-11 nm2/KG2
g=G M R 2 = 4π 3 GpR
dane: stałe G są warte 6.67 * 10-11 nm2 / kg2
Księżyc
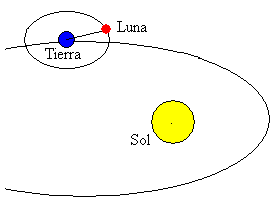
Księżyc jest jednym z największych ciał Układu Słonecznego. Jego orbita jest prawie okrągła (mimośrodowość ε=0,05), a płaszczyzna jego orbity jest nachylona o 5 ° w stosunku do płaszczyzny orbity Ziemi.
średnia odległość między środkiem ziemi a Księżycem wynosi 384 400 KM. jego okres obrotu wokół Ziemi wynosi 27 322 dni. Zmiana położenia Księżyca względem słońca prowadzi do faz księżyca.
księżyc zawsze przedstawia tę samą twarz obserwatorowi ziemi ze względu na wpływ sił pływowych, jakie Ziemia wywiera na Księżyc. Oznacza to, że zbiega się okres obrotu Księżyca wokół własnej osi i czas potrzebny do ukończenia orbity wokół Ziemi.
Księżyc jest obiektem niebieskim, który najbardziej oczarował gatunek ludzki. Były Związek Radziecki po raz pierwszy wysłał automatyczny statek, który wylądował na powierzchni Księżyca w 1959 roku. 20 lipca 1969 r.Neil Armstrong w towarzystwie Edwina Aldrina byli pierwszymi ludźmi, którzy chodzili po powierzchni Księżyca w ramach misji Apollo 11. Ostatnia wizyta amerykańskich astronautów na Księżycu miała miejsce w 1972 roku.
pochodzenie księżyca wygląda niepewnie, istnieje kilka teorii:
-
Co ona powstała w tym samym czasie, że Ziemia jest z materiału z mgławicy
-
Że ciało Niebieskie zostało podzielone na dwie części, dając pochodzenia Ziemi i Księżyca
-
Że Księżyc powstał w innym miejscu i został schwytany Ziemi
-
Że Ziemia zderzył się z ciał niebieskich dużych rozmiarów (wielkości Marsa lub wyżej) i, że Księżyc powstał, materiał wyrzucony z tego starcia.
ta ostatnia teoria wydaje się być teraz bardziej akceptowane w środowisku naukowym.
trajektoria Księżyca
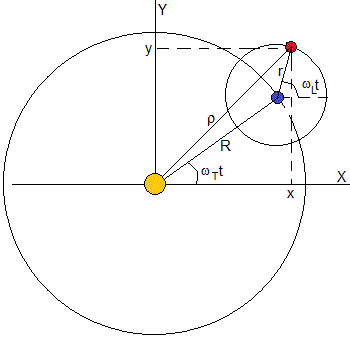
rozważ planetę i jej satelitę. Planeta opisuje orbitę kołową o promieniu R wokół swojej gwiazdy o stałej prędkości kątowej wT = 2π / PT, przy czym PT jest okresem lub czasem, w którym osiąga pełny obrót. Towarzysz opisuje orbicie kołowej coplanaria promieniu r ze stałą prędkość kątową wL=2π/PL, będąc PL okres lub czas potrzebny na pełny obrót
położenie satelity w stosunku do układu odniesienia, źródłem których jest gwiazda, jest
x=Rcos( ω T )+rcos( ω L t), y=Rsin( ω T )+rsin( ω L t )
Sea α=wT/wL
{ x=Rcos( α, ω, L, t )+rcos( ω L t), y=Rsin( α, ω, L, t )+rsin( ω L t ) { x=Rcos( α 2π P L t )+rcos( 2π P L t), y=Rsin( α 2π P L t )+rsin( 2π P L t )
Nazwijmy τ=t/PL
x =R cos( α·2πτ )+ r cos( 2πτ ) i R =sin( α·2πτ )+ r sin( 2πτ )
przedstawiamy trajektorię satelity dla α=0.1 i dla trzech wartości współczynnika r/R.
- r/r<α. Przykład, r / r=0.05
- r / r=α. Przykład, r / r=0.1
- r / r> α. Na przykład r/R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
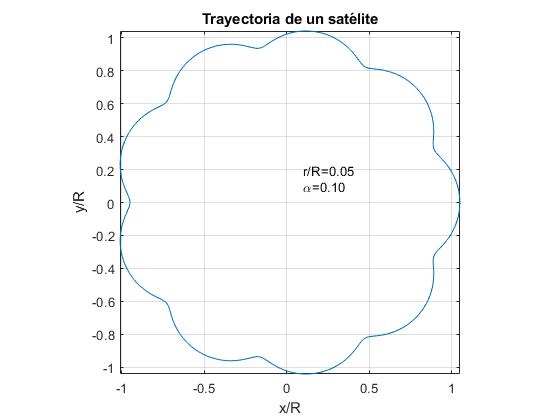
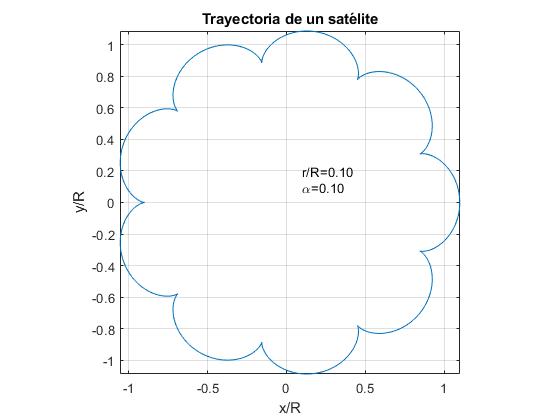
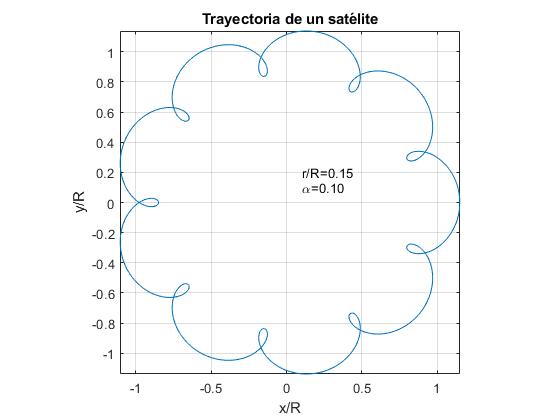
w przypadku Ziemi i Księżyca dane:
- promień orbity Księżyca r = 384.4 * 106 m, okres PL = 27.32 d
- promień orbity Ziemi: R=149.6·109 m, okres PT=365.26 d
α=wT/wL=PL/PT=0.0748. R / R=0.0026
orbita Księżyca będzie na pierwszym rysunku. W graficzne przedstawienie trajektorii Księżyca, aby te wartości α i r/R, nie doceniają wahania promieniowego odległości między Słońcem i Księżycem
Przyspieszenie Księżyca
odległość ρ od Słońca do Księżyca
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T), t )
Obliczyć składniki, prostokątne, przyspieszenie
{ dx dt =− ω T Rsin( ω T (t )− ω L rsin( ω L t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T (t )− ω L 2 rcos( ω L (t ) i = d 2 d t 2 =− ω T 2 Rsin( ω T (t )− ω L 2 rsin( ω L t )
promieniową składową przyspieszenia
a ρ = a → · ρ → ρ = a x+ a x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2rR cos( ( ω L − ω T), t )
minimalne i maksymalne wartości są uzyskiwane przy cos((wL-wT)t)=±1
max =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2rR =−( ω T 2 R+ ω L 2 r ) a min =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 −2rR =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
Księżyc jest jedynym satelitą Układu Słonecznego, którego promieniowy Składnik przyspieszenia jest ujemny, mówi się, że ’ księżyc spada w kierunku słońca ’
Fazy księżyca
rysunek pokazuje Księżyc w różnych pozycjach jego orbity wokół Ziemi. Słońce daleko oświetla oba ciała niebieskie (u góry rysunku)
połowa Księżyca jest oświetlona przez słońce (w kolorze białym), a połowa Księżyca najbliższego Ziemi jest widoczna przez obserwatora ziemi. Ponieważ księżyc porusza się wokół Ziemi widzimy różne frakcje, część strefy nasłonecznionej w Kolorze Żółtym).
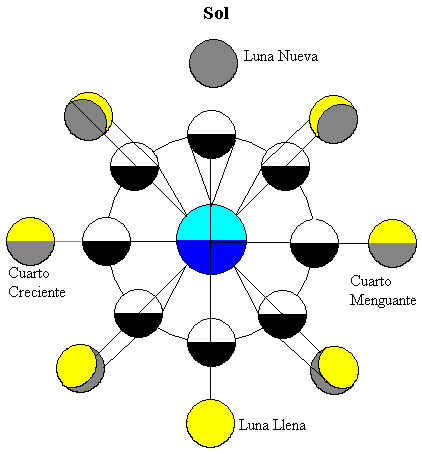
-
kiedy Księżyc znajduje się między Ziemią a Słońcem część Księżyca najbliższego ziemi jest ciemna, więc nie możemy zobaczyć Księżyca, faza ta nazywa się nowiu.
-
kiedy Ziemia znajduje się między Słońcem a Księżycem, część Księżyca najbliżej ziemi jest połowa oświetlona, faza ta nazywa się pełnią księżyca.
-
kiedy Księżyc znajduje się w pozycjach pośrednich, tylko połowa części najbliższej Ziemi jest oświetlona. Widzimy więc tylko jedną czwartą Księżyca, te dwie fazy nazywane są ćwiartkami rosnącymi lub malejącymi w zależności od tego, czy oświetlona część widoczna z Ziemi ma tendencję wzrostową lub malejącą.
Uwaga: Ten interaktywny program próbuje wyjaśnić Fazy księżyca, ale nie jest to prawdziwa reprezentacja orbity Księżyca, który tworzy kąt 5 ° do płaszczyzny ekliptyki (orbity Ziemi wokół Słońca), ani od orientacji osi Ziemi, która jest w przybliżeniu 23 ° C do płaszczyzny ekliptyki.
wytyczono czerwoną linię, która przecina Księżyc, aby czytelnik mógł ocenić, czy okres obrotu Księżyca odpowiada jego osi i czasowi, jaki zajmuje Ukończenie jednej orbity wokół Ziemi, a zatem Księżyc ma zawsze ta sama twarz do ziemi.
zaćmienia Księżyca
zaćmienia Księżyca występują zawsze, że Księżyc jest w fazie jest wypełniona i pod warunkiem, że Słońce, Ziemia i Księżyc są w linii prostej. Tak więc Księżyc znajduje się w cieniu wytwarzanym przez ziemię, jak pokazano na rysunku.
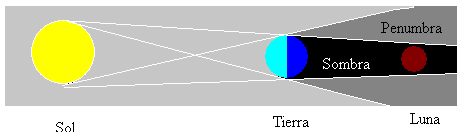
istnieją inne rodzaje zaćmienia Księżyca, które zależą od wyrównania trzech ciał niebieskich. Księżyc może znajdować się w nieoświetlonej (cieniu) lub częściowo oświetlonej (półcieniu) strefie.
zaćmienie Słońca ma miejsce, gdy Księżyc stoi między Słońcem a Ziemią, Księżyc znajduje się w nowej fazie. Księżyc jest 400 razy mniejszy niż słońce, ale Księżyc jest 400 razy bliżej Ziemi, więc pozorny rozmiar obu ciał widziany z Ziemi jest prawie taki sam. Księżyc może zatem spowodować zaćmienie Słońca, jeśli obserwuje się w strefie cienia rzutowanej z księżyca na Ziemię.
dane Księżyca
| Masa (kg) | 7.349·1022 |
| Promień (km) | 1737. 4 |
| średnia gęstość (g / cm3) | 3.34 |
| średnia Odległość od Ziemi (km) | 384 000 |
| Okres obrotu (dni) | 27.32166 |
| Przyspieszenie siły ciężkości na równiku (m/s2) | 1.62 |
| Mimośród orbity | 0.0549 |
| Nachylenie orbity (stopnie) | 5.1454 |
-
Obliczyć promień kołowej orbicie Księżyca wokół Ziemi, wiedząc, że okres ten wynosi 27.32 dni. Oblicz także prędkość Księżyca. Dane: g =6.67 * 10-11 Nm2 / kg2, masa Ziemi M=5.98·1024 kg.
-
Oblicz przyspieszenie grawitacji g na powierzchni Księżyca.
-
Oblicz zależność między średnicą słońca a średnicą Księżyca. Oblicz zależność między średnią odległością między Słońcem a Ziemią, a Księżycem i ziemią. Dane: promień słońca 6.96 * 108 M, średnia odległość Ziemi-Słońce 1.49 * 1011 m
-
Oblicz położenie środka masy układu Ziemia-Księżyc mierzone od środka Ziemi.
-
Oblicz siłę przyciągania Ziemi na Księżycu i porównaj ją z siłą przyciągania słońca na Księżycu. Fakt: masa Słońca, 1.98 * 1030 kg
Literatura
m. Marow. Planety Układu Słonecznego. Wydawnictwo Mir.
więcej o planetach na ile planet w naszym Układzie Słonecznym?. ComofuncionaQue.com
dla sekcji 'trajektoria Księżyca’
David K. Johnston. Cycloidal paths in physics as superpositions of translational and rotational motions. Am. J. Phys.87 (10), październik 2019, S. 808-810
księżyc zawsze odwraca się w kierunku słońca. Strony z matematyką.