a utilização de logaritmos no mundo Real
logaritmos está em todo o lado. Já usou as seguintes frases?
- 6 figuras
- dígitos Duplos
- Ordem de grandeza
- taxa de Juros
Você está descrevendo números em termos de potências de 10, um logaritmo. E uma taxa de juros é o logaritmo do crescimento de um investimento.Surpreendido por os logaritmos serem tão comuns? Eu também. A maioria das tentativas de matemática no mundo Real (TM) apontam logaritmos em alguma fórmula Arcana, ou fingem que somos geólogos fascinados pela escala de Richter. “Os cientistas preocupam-se com troncos, e tu também devias. Além disso, consegues imaginar um mundo sem zinco?”
No, no, no, no, no, no! (Mama mia!)
a matemática expressa conceitos com notação como “ln”ou ” log”. Encontrar “matemática no mundo real” significa encontrar ideias na vida e ver como elas podem ser escritas com notação. Não procures símbolos literais! Quando foi a última vez que escreveste um sinal da divisão? Quando foi a última vez que cortaste comida?Ok, ok, já percebemos: o que são os logaritmos?
os logaritmos encontram a causa para um efeito, ou seja, a entrada para algum resultado
um “efeito” comum é ver algo crescer, como ir de \$100 a \$150 em 5 anos. Como é que isto aconteceu? Não temos certeza, mas o logaritmo encontra uma possível causa: um retorno contínuo de ln(150/100) / 5 = 8,1% seria responsável por essa mudança. Pode não ser a causa real (todo o crescimento aconteceu no último ano?), mas é uma média suave que podemos comparar com outras mudanças.
a propósito, a noção de “causa e efeito” é matizada. Porque é 1000 maior que 100?
- 100 é 10, que cresceu por si só para 2 períodos de tempo ($10 * 10$)
- 1000 é 10, que cresceu por si só para 3 períodos de tempo ($10 * 10 * 10$)
podemos pensar em números como saídas (1000 é “1000 saídas”) e entradas (“quantas vezes não 10 precisa crescer para fazer essas saídas?”). Então … ,
1000 outputs > 100 outputsporque
3 inputs > 2 inputsou por outras palavras:
log(1000) > log(100)porque é que isto é útil?
os logaritmos colocam os números numa escala amiga do homem.Grandes números partem-nos o cérebro. Milhões e triliões são “realmente grandes”, mesmo que um milhão de segundos seja 12 dias e um trilião de segundos seja 30.000 anos. É a diferença entre um ano de férias americano e toda a civilização humana.
o truque para superar ” cegueira de números enormes “é escrever números em termos de” entradas ” (ou seja, sua base de poder 10). Esta escala menor (0 a 100) é muito mais fácil de compreender:
- poder de 0 = $10^0$ = 1 (item único)
- poder de 1 = $10^1$ = 10
- potência de 3 = $10^3$ = mil
- potência de 6 = $10^6$ = milhões de
- o poder dos 9 = $10^9$ = mil milhões de
- potência de 12 = $10^12$ = trilhões
- potência de 23 = $10^23$ = número de moléculas em uma dúzia de gramas de carbono
- poder de 80 = $10^80$ = número de moléculas no universo
0 80 escala levou-nos a partir de um único item para o número de coisas no universo. Nada mal.
logaritmos contar a multiplicação como passos
logaritmos descrever alterações em termos de multiplicação: nos exemplos acima, cada passo é 10x maior. Com o log natural, cada passo é ” e ” (2,71828…) vezes mais.
ao lidar com uma série de multiplicações, os logaritmos ajudam a “contá-los”, assim como a adição conta para nós quando os efeitos são adicionados.Mostra-me a matemática, 2232, 3924, hora da carne. vamos ver onde aparecem os logaritmos!
salário de seis dígitos ou despesa de dois dígitos
estamos descrevendo números em termos de seus dígitos, i.e. quantos poderes de 10 eles têm (eles estão nas dezenas, centenas, milhares, dez-milhares, etc.). A adição de um dígito significa “multiplicando por 10”, i.é.
![]()
Logaritmos contar o número de multiplicações adicionadas, assim, começando com 1 (um dígito) vamos adicionar 5 dígitos (us$10^5$) e 100.000 obter um 6-figura de resultado. Falar de ” 6 “em vez de” cem mil ” é a essência dos logaritmos. Dá um senso de escala sem saltar em detalhes.Pergunta bónus: como Descreveria 500.000? Dizer “6 dígitos”é enganador porque 6 números muitas vezes implica algo mais próximo de 100.000. “6.5 dígitos” funcionaria?Nem por isso. Em nossas cabeças, 6.5 significa “meio caminho” entre 6 e 7 dígitos, mas essa é a mentalidade de um adder. With logarithms a”.5 ” significa metade em termos de multiplicação, ou seja, a raiz quadrada ($9^.5$ significa que a raiz quadrada de 9 — 3 está a meio caminho em termos de multiplicação porque é de 1 a 3 e 3 a 9).
tomando log (500.000) nós obtemos 5.7, adicionamos 1 para o dígito extra, e podemos dizer “500.000 é um 6.7 figure number”. Experimente aqui:
ordem de magnitude
Nós, geeks, adoramos esta frase. Significa aproximadamente “diferença de 10x”, mas apenas soa mais fresco do que”um dígito maior”.
em computadores, onde tudo é contado com bits (1 ou 0), cada bit tem um efeito de duplicação (não 10x). Então indo de 8 para 16 bits é “8 ordens de magnitude” ou $2^8 = 256$ vezes maior. (“Maior” neste caso refere-se à quantidade de memória que pode ser endereçada.) Indo de 16 para 32 bits significa um extra de 16 ordens de magnitude, ou $ 2^16$ ~ 65,536 vezes mais memória que pode ser endereçada.
taxas de juro
como se calculam as taxas de crescimento? Um país não pretende crescer a 8,56% ao ano. Olhamos para o PIB num ano e para o PIB no outro, e pegamos no logaritmo para encontrar a taxa de crescimento implícita.
Meus dois favoritos interpretações do logaritmo natural (ln(x)), i.e. o log natural de 1.5:
- Supondo 100% de crescimento, quanto tempo você precisa para crescer para chegar a 1.5? (.405, menos de metade do período de tempo)
- assumindo 1 unidade de tempo, quão rápido você precisa crescer para chegar a 1,5? (40.5% por ano, em composição contínua)
os logaritmos são a forma como descobrimos a rapidez com que estamos a crescer.
escala de medição: o Google PageRank
o Google dá a cada página da web uma pontuação (PageRank) que é uma medida aproximada de autoridade / importância. Esta é uma escala logarítmica, que em minha cabeça significa “PageRank conta o número de dígitos em sua pontuação”.
So, a site with pagerank 2 (“2 dígitos”) is 10x more popular than a PageRank 1 site. O meu site é PageRank 5 e a CNN tem PageRank 9, por isso há uma diferença de 4 ordens de magnitude.($10^4$ = 10,000).Em termos gerais, recebo cerca de 7000 visitas por dia. Usando a matemática do meu envelope, posso adivinhar que a CNN recebe cerca de 7000 * 10,000 = 70 milhões de visitas / dia. Como é que eu fiz isso? Na minha cabeça, acho que $ 7k * 10k = 70 * k * K = 70 * m$). Eles podem ter algumas vezes mais do que isso (100M, 200M), mas provavelmente não até 700M.
o Google transmite muitas informações com uma escala muito áspera (1-10).Escala de medição: Richter, Decibel, etc.
suspiro. Estamos no exemplo típico de “logaritmos no mundo real”: escala de Richter e Decibel. A idéia é colocar eventos que podem variar drasticamente (terremotos) em uma única escala com uma pequena escala (tipicamente 1 a 10). Assim como PageRank, cada aumento de 1 ponto é uma melhoria de 10x no poder. O maior terremoto registrado pelo homem foi de 9,5; o impacto da Península de Iucatã, que provavelmente fez os dinossauros extintos, foi de 13.
decibéis são semelhantes, embora possam ser negativos. Os sons podem ir de intensamente silenciosos (pindrop) para extremamente barulhentos (avião) e nossos cérebros podem processar tudo. Na realidade, o som do motor de um avião é milhões (bilhões, trilhões) de vezes mais poderoso do que uma pindrop, e é inconveniente ter uma escala que vai de 1 a um milhão. Os registos mantêm tudo numa escala razoável.
grafos logarítmicos
você frequentemente verá itens plotados em uma “escala logarítmica”. Na minha cabeça, isso significa que um lado está contando “número de dígitos” ou “número de multiplicações”, não o valor em si. Mais uma vez, isso ajuda a mostrar eventos muito variados em uma única escala (indo de 1 a 10, não 1 A bilhões).A lei de Moore é um grande exemplo: dobramos o número de transistores a cada 18 meses (Imagem cortesia Wikipedia).
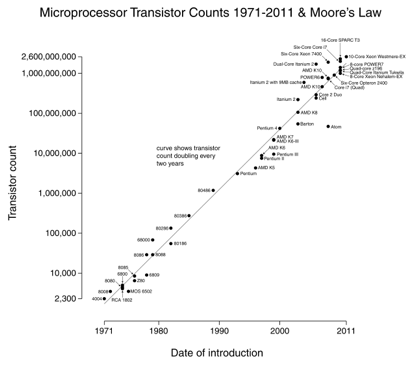
The neat thing about log-scale graphs is exponential changes (processor speed) appear as a straight line. Crescer 10x por ano significa que estás constantemente a subir a escala dos “dígitos”.
para a frente e para cima
se um conceito é bem conhecido mas não bem amado, significa que precisamos construir a nossa intuição. Encontra as analogias que funcionam, e não te contentes com a porcaria de um livro vai sair. Na minha cabeça:
- logaritmos encontram a causa raiz de um efeito (Ver crescimento, encontrar taxa de juro)
- ajudam a contar multiplicações ou dígitos, com o bónus de contagens parciais (500k é um número de 6,7 dígitos))
boa matemática.
Outros Posts Desta Série
- Uma interface Intuitiva Guia De Funções Exponenciais & e
- Desmistificando o Logaritmo Natural (ln)
- Um Guia Visual Simples, Composto e Contínua Taxas de Juros
- Definições Comuns de e (Colorida)
- Compreensão Expoentes (Por que 0^0 = 1?)
- Using Logarithms in The Real World
- How To Think With Exponents And Logarithms
- Understanding Discrete vs. Continuous Growth
- What does an exponent really mean?
- Q: Por que é o e especial? (2.718…, não 2, 3.7 ou outro número?)