Bootstrap in R
Bootstrap is a method of inference about a population using sample data.Bradley Efron introduziu-o pela primeira vez neste papel em 1979.O Bootstrap baseia-se na amostragem com substituição dos dados da amostra. Esta técnica pode ser utilizada para estimar o erro-padrão de qualquer estatística e para obter um intervalo de confiança (IC) para ela. Bootstrap é especialmente útil quando o IC não tem uma forma fechada, ou tem uma muito complicada.
suponha que temos uma amostra de elementos n:X = {x1, x2, …, xn} e estamos interessados em CI para alguma estatística T = t(X). O quadro de arranque é simples. Repetimos R vezes o seguinte esquema: para a repetição i-th, amostra com elementos n de Substituição Da Amostra Disponível (alguns deles serão escolhidos mais de uma vez). Invoca esta nova amostra i-ésima amostra de bootstrap, Xi, e calcula a estatística necessária Ti = t(Xi).
como resultado, obteremos valores R da nossa estatística: T1, T2,…, TR. Nós chamamos de realizações de T ou uma distribuição de bootstrap de T. Com base nisso, podemos calcular CI para T. há várias maneiras de fazer isso. Tomar percentis parece ser o mais fácil.
Bootstrap in action
Let’s use (once again) well-known iris dataset. Veja as primeiras filas:
suponha que queremos encontrar CIs para a mediana Sepal.Length, medianaSepal.Width e coeficiente de correlação de rank de Spearman entre estas duas. Vamos usar R‘s boot pacote e uma função chamada… boot. Aumentar o seu poder temos de criar uma função que calcula o(s) Nosso (s) estatistico (s) a partir de dados recolocados. Deve ter pelo menos duas argolas: a dataset e um vetor contendo indices de elementos de um conjunto de dados que foram escolhidos para criar uma amostra de bootstrap.
se quisermos calcular CIs para mais de uma estatística de uma vez, a nossa função tem de Os devolver como um único vector.
Para o nosso exemplo, ele pode ser como esta:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo escolhe os elementos desejados (que números são armazenados em indices)de data e calcula o coeficiente de correlação das duas primeiras colunas(method='s' é usado para escolher Spearman rank coeficientemethod='p' vai resultado com o de Pearson coeficiente) e suas medianas.
também podemos adicionar alguns argumentos extra, por exemplo. deixar o utilizador escolher o coeficiente de odcorrelação do tipo:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )} para tornar este tutorial mais geral, vou usar a última versão de foo.
agora, podemos usar a função boot. Temos que fornecê-lo com um nome oddataset, função que acabamos de criar, número de repetições (R)e quaisquer argumentos adicionais de nossa função (como cor.type). Abaixo, utiliza-se set.seed para a reprodutibilidade deste exemplo.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot a função devolve um objecto da classe chamada… (sim, tens razão!)boot. Tem dois elementos interessantes. $t contém valores R da(s) Nossa (s) estatística (s) gerada (s) pelo procedimento bootstrap (realizações bootstrap muitas vezes):
$t0 contém os valores da(S) nossa (S) estatística (s) no conjunto de dados original, completo:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000imprimir boot objecto na consola dá mais algumas informações:
original é igual a $t0. bias é uma diferença entre a média das realizações de bootstrap (as de $t), chamada de uma estimativa de bootstrap de T e valor no conjunto de dados originais (a de $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error is a standard error of bootstrap estimate, which equalsstandard deviation of bootstrap realizations.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414diferentes tipos de bootstrap CIs
Antes de começarmos com IC, vale sempre a pena dar uma olhada na distribuição das realizações bootstrap. Nós podemos usar plot função, com index dizendo em qual das estatísticas computadas em foo nós desejamos tolook. Aqui index=1 é um coeficiente de correlação de Spearman entre comprimento e largura, index=2 é um comprimento sepal médio eindex=3 é uma largura sepal média.
plot(myBootstrap, index=1)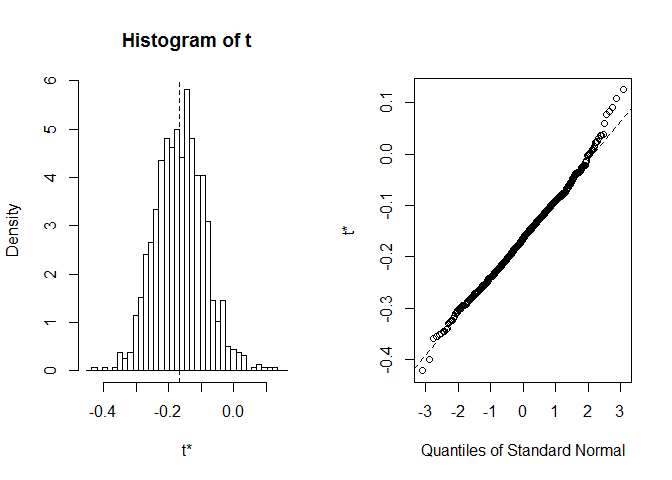
distribuição de coeficientes de correlação bootstrap parece quitenormal. Vamos procurar o Informador. Podemos usar boot.ci. O padrão é 95% CIs, mas pode ser alterado com o parâmetro conf.
boot.ci fornece 5 tipos de IC bootstrap. Um deles, studentizedinterval, é único. Precisa de uma estimativa da variância do bootstrap. R imprime um aviso:bootstrap variances needed for studentized intervals. As estimativas de variância podem ser obtidas com bootstrap de segundo nível ou (mais fácil) com a técnica de Jackknife. Isto está de alguma forma além do escopo deste tutorial,então vamos nos concentrar nos quatro tipos restantes de bootstrap CIs.
se não queremos vê-los todos, podemos escolher os relevantes em typeargumento. Os valores possíveis são:norm, basic, stud, perc, bca um vector destes.
a função boot.ci cria objeto de classe… (Sim, você adivinhou!)bootci. Seus elementos são chamados assim como tipos de IC usados em typeargumento. $norm é um vector de 3 elementos que contém limites de confiança leveland.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc e $bca 5-elemento de vetores containingalso percentis utilizados para calcular CI (voltaremos a isso mais tarde):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178Um pouco de notação (Desculpe!)
para termos uma ideia dos diferentes tipos de IC, precisamos de introduzir uma notação. Então, vamos:
- t⋆ ser o bootstrap estimativa (média de bootstraprealizations),
- t0 ser um valor da estatística do conjunto de dados original,
- se⋆ ser um erro padrão da estimativa bootstrap,
- b ser um viés de bootstrap estimateb = t⋆ − t0
- α ser um nível de confiança de, normalmente α = 0.95,
- za ser um us $1\frac \alpha 2$-gráfico quantil de standardnormal de distribuição,
- θα ser uma α-percentil da distribuição de bootstraprealizations.
percentil CI
com notação acima, percentil CI é:
então, isto requer apenas percentis relevantes. Nada mais.
IC Normal
um IC Wald típico seria:
mas no caso do bootstrap, devemos corrigi-lo por preconceito. Torna-se assim:
$$ t_0 – b \pm z_\alpha \cdot se^\estrelas \\2t_0 – t^\estrelas \pm z_\alpha \cdot se^\star$$
Basic CI
Percentil CI geralmente não é recomendada, pois ela executa poorlywhen vem a estranha distribuições com caudas. O IC básico (também chamado de IC empírico ou calledpivotal) é muito mais robusto para isso. O raciocínio consiste em calcular as diferenças entre cada replicação de bootstrap e t0 e utilizar percentis da sua distribuição. Fulldetails pode ser encontrado, por exemplo, em L. Wasserman Tudo ofStatistics
Final de fórmula básica CI é:
BCa CI
BCa vem de bias-corrected, acelerado. A fórmula não é muito complicada, mas um pouco não intuitiva, por isso vou ignorá-la.Ver artigo de Thomas J. DiCiccio e BradleyEfron, se estiverem interessados em detalhes.
aceleração mencionada no nome do método requer o uso de características específicas de realizações de bootstrap. Às vezes pode acontecer que estes seriam alguns percentis extremos, possivelmente anómalos.A ACB pode ser instável em tais casos.
vamos olhar para o IC BCa para a mediana da largura das pétalas. Conjunto de dados Inoriginal, esta mediana é igual precisamente a 3.
ficamos com CI BCa (2.9, 2.9). Isso é estranho, mas felizmente R nos avisou que extreme order statistics used as endpoints. Vamos ver o que aconteceu aqui.:
plot(myBootstrap, index=3)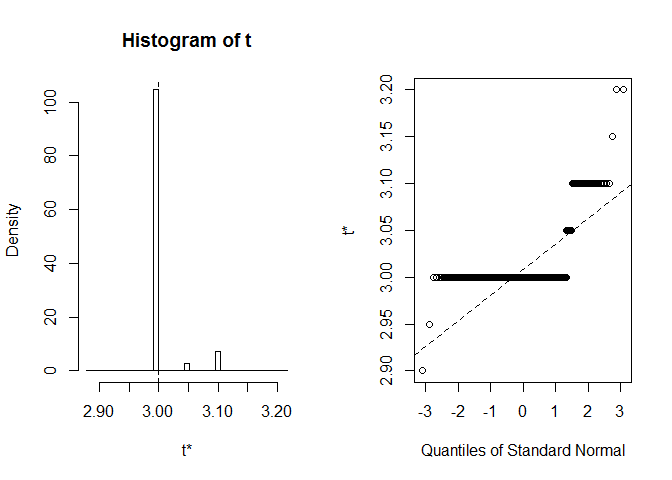
distribuição de realizações de bootstrap é incomum. Uma grande maioria deles (mais de 90%) são 3.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2replicação de resultados
às vezes, precisamos recriar replicações de bootstrap. Se podemos usar R para ele, isso não é um problema. set.seed a função resolve o problema.Recriar replicações de bootstrap em outro software seria muito mais complicado. O que é mais, para R grande, recálculo em R pode alsonot ser uma opção (devido à falta de tempo, por exemplo).
podemos lidar com este problema, economizando índices de elementos do originaldataset, que formaram cada amostra de bootstrap. Isto é o que boot.arrayfunção (com indices=T argumento) faz.
tableOfIndices<-boot.array(myBootstrap, indices=T)cada linha é uma amostra de bootstrap. Exemplo., nossa primeira amostra contém os seguintes elementos:
Setting indices=F (um padrão), vamos obter uma resposta para a Pergunta “Quantas vezes cada elemento do conjunto de dados originais apareceu em cada bootstrapsample?”. Por exemplo, na primeira amostra: o primeiro elemento do conjunto de dados apearedonce, o segundo elemento não apareceu de todo, o terceiro elemento apareceu uma vez, o quarto Duo e assim por diante.
uma tabela como esta permite recriar a realização de bootstrap fora R.Ou em R quando não queremos usar set.seed e fazer toda a computação mais uma vez.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')vamos verificar se os resultados são os mesmos:
Sim, são!
se você gostaria de aprender mais sobre a aprendizagem de máquinas em R, faça o curso DataCamp da caixa de ferramentas de aprendizagem de máquinas.