Diferença entre IIR e FIR filtros: um prático guia de design

de Um filtro digital é um algoritmo matemático que opera sobre um conjunto de dados digitais (e.g. sensor de dados), a fim de extrair informações de interesse e remover qualquer informação indesejada. Aplicações deste tipo de tecnologia, incluem a remoção de falhas dos dados dos sensores ou até mesmo a limpeza do ruído em um sinal medido para uma análise de dados mais fácil. Mas como escolhemos o melhor tipo de filtro digital para a nossa aplicação? E quais são as diferenças entre um filtro IIR e um filtro FIR?

filtros Digitais são divididos em duas categorias a seguir:

• Infinito resposta ao impulso (IIR)
• Finite impulse response (FIR)

Como os nomes sugerem, cada tipo de filtro é classificado pelo comprimento de sua resposta ao impulso. No entanto, antes de começar com uma análise matemática detalhada, é prudente apreciar as diferenças de desempenho e características de cada tipo de filtro.

exemplo

a fim de ilustrar as diferenças entre um IIR e o FIR, a resposta de frequência de um FIR de 14a ordem (linha sólida), e um Chebyshev Tipo IIR de 4a ordem (linha tracejada) é mostrado abaixo na Figura 1. Observe que, embora os espectros de magnitude tenham um grau de atenuação semelhante, o espectro de fase do filtro IIR é não-linear na banda de passagem (\(\pequeno 0\rightarrow7.5Hz\)), e torna-se muito não-linear na frequência de corte, \(\pequeno f_c=7,5 Hz\). Observe também que o FIR requer um maior número de coeficientes (15 vs 10 do IIR) para corresponder às características de atenuação do IIR.

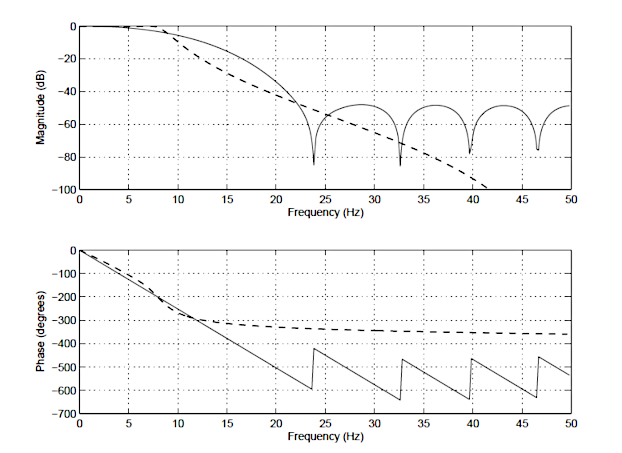
Estas são apenas algumas das diferenças entre os dois tipos de filtros. Segue-se um resumo detalhado das principais vantagens e desvantagens de cada tipo de filtro.

filtros IIR

IIR (infinite impulse response) filtros são geralmente escolhidos para aplicações onde a fase linear não é muito importante e a memória é limitada. Eles têm sido amplamente utilizados na equalização do som, biomédica, processamento de sinal do sensor, IoT/IIoT sensores inteligentes e de alta velocidade de telecomunicações/aplicações de RF.

> Vantagens

• Baixo custo de implantação: requer menos coeficientes e memória do que os filtros FIR para satisfazer um conjunto semelhante de especificações, ou seja, frequência de corte e atenuação da fita.
• baixa latência: adequada para o controlo em tempo real e aplicações RF de muito alta velocidade devido ao baixo número de coeficientes.
• equivalente analógico: pode ser utilizado para imitar as características dos filtros analógicos que utilizam a transformação do mapeamento Plano s-Z.

desvantagens

• características de fase não linear: As características de fase de um filtro IIR são geralmente não lineares, especialmente perto das frequências de corte. Podem ser utilizados filtros de equalização de passagem única para melhorar as características da fase de passagem.
• análise mais detalhada: requer maior escala e análise de transbordamento numérico quando implementado em ponto fixo. A estrutura direta do filtro de forma II é especialmente sensível aos efeitos da quantização e requer especial cuidado durante a fase de projeto.
• estabilidade numérica: Menos estável numericamente do que suas contrapartes FIR (resposta de impulso finito), devido aos caminhos de feedback.Os filtros FIR (finite impulse response) são geralmente escolhidos para aplicações onde a fase linear é importante e uma quantidade decente de memória e desempenho computacional estão disponíveis. Eles têm uma ampla implantação em aplicações de áudio e melhoria de sinal biomédico. Sua estrutura all-zero (discutido abaixo) garante que eles nunca se tornam instáveis para qualquer tipo de sinal de entrada, o que lhes dá uma vantagem distinta sobre o IIR.

  vantagens

  • fase Linear: FIRs pode ser facilmente projetado para ter fase linear. Isto significa que nenhuma distorção de fase é introduzida no sinal a ser filtrado, uma vez que todas as frequências são desviadas no tempo pela mesma quantidade – mantendo assim as suas relações harmônicas relativas (ou seja, atraso constante de grupo e fase). Este não é certamente o caso dos filtros IIR, que têm uma característica de fase não linear.
  • estabilidade: como FIRs não usam valores de saída anteriores para calcular sua saída atual, i.e. eles não têm feedback, eles nunca podem se tornar instáveis para qualquer tipo de sinal de entrada, o que lhes dá uma vantagem distinta sobre os filtros IIR.
  • Arbitrary frequency response: the Parks-McClellan and ASN Filterscript’s firarb() function allow for the design of an FIR with an arbitrary magnitude response. Isto significa que um abeto pode ser personalizado mais facilmente do que um abeto.
  • desempenho em ponto fixo: os efeitos de quantização são menos graves do que os de uma IIR.

  desvantagens

  • elevada exigência computacional e de memória: Os FIRs geralmente requerem muito mais coeficientes para alcançar um corte afiado do que seus homólogos do IIR. A consequência disso é que eles requerem muito mais memória e significativamente uma maior quantidade de operações MAC (múltiplas e acumuladas). No entanto, arquiteturas modernas de microcontroladores baseados nos núcleos córtex-M do Arm agora incluem suporte de hardware DSP via SIMD (instrução de sinal, múltiplos dados) que agilizam a operação de filtragem significativamente.
  • latência superior: o maior número de coeficientes, significa que, em geral, um FIR é menos adequado do que um IIR para aplicações de alta velocidade. Isto torna-se problemático para aplicações de controle em tempo real em ciclo fechado, onde um filtro FIR pode ter muito atraso de grupo para alcançar a estabilidade de loop.
  • nenhum equivalente analógico: usando o Bilinear, combinado z-transform( mapeamento s-z), um filtro analógico pode ser facilmente transformado em um filtro IIR equivalente. No entanto, isso não é possível para um abeto, uma vez que não tem equivalente analógico.

  definições Matemáticas

  Como discutido na introdução, o nome IIR e FIR são originários da matemática definições de cada tipo de filtro, por exemplo, um filtro IIR é classificada por seu teoricamente infinito de impulso resposta,

  \(\displaystyle
  y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
  \)

  e um ABETO classificados pela sua resposta ao impulso finita,

  \(\displaystyle
  y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
  \)

  Vamos agora analisar as propriedades matemáticas de cada tipo de filtro em volta.

  IIR definição

  Como visto acima, um filtro IIR é classificada por seu teoricamente infinito de impulso resposta,

  \(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)

  Praticamente falando, não é possível calcular a saída de uma IIR usando esta equação. Portanto, a equação pode ser reescrita em termos de um número finito de polos \(\pequeno p\) e zeros \(\pequeno q\), como definido pela equação de diferença de coeficiente constante linear dada por:

  \(\displaystyle
  y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
  \)

  onde \(\small a_k\) e \(\small b_k\) são o filtro do denominador e numerador coeficientes polinomiais, que raízes são iguais para o filtro de pólos e zeros, respectivamente. Assim, uma relação entre a diferença de equação e a transformada z (função de transferência), portanto, podem ser definidos usando a transformada z de atraso de propriedade tal que,

  \(\displaystyle
  \sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
  \)

  Como visto, a função de transferência é uma representação no domínio da frequência do filtro. Observe também que os polos atuam nos dados de saída, e os zeros nos dados de entrada. Uma vez que os polos atuam sobre os dados de saída, e afetam a estabilidade, é essencial que seus raios permaneçam dentro do círculo unitário (ou seja, <1) para a estabilidade de BIBO (entrada limitada, saída limitada). Os raios dos zeros são menos críticos, pois não afetam a estabilidade do filtro. Esta é a principal razão pela qual os filtros FIR all-zero (resposta de impulso finito) são sempre estáveis.

  BIBO estabilidade

  linear invariante no tempo (LTI) sistema (como um filtro digital) é dito ser limitado de entrada, limitada a saída estável, ou BIBO estável, se cada limitada de entrada dá origem a um limitado saída, como

  \(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \)

  Onde, \(\small h(k)\) é o LTI do sistema de resposta ao impulso. Analisando esta equação, deve ficar claro que o critério de estabilidade de BIBO só será satisfeito se os polos do sistema estiverem dentro do círculo unitário, uma vez que o ROC do sistema (região de convergência) deve incluir o círculo unitário. Consequentemente, é suficiente dizer que um sinal de entrada limitado sempre produzirá um sinal de saída limitado se todos os polos estiverem dentro do círculo unitário.

  os zeros, por outro lado, não são restringidos por este requisito, e como consequência pode estar em qualquer lugar no plano z, Uma vez que eles não afetam diretamente a estabilidade do sistema. Portanto, uma análise de estabilidade do sistema pode ser realizada primeiramente calculando as raízes da função de transferência (isto é, raízes do numerador e polinômios do denominador) e então plotando os pólos e zeros correspondentes sobre o plano z.

  uma situação interessante surge se quaisquer polos se encontram no círculo unitário, uma vez que o sistema é dito ser marginalmente estável, uma vez que não é nem estável ou instável. Embora os sistemas marginalmente estáveis não sejam BIBO estáveis, eles têm sido explorados por designers de osciladores digitais, uma vez que sua resposta de impulso fornece um método simples de geração de ondas sine, que provou ser inestimável no campo das telecomunicações.

  Biquad filtros IIR

  A implementação de um filtro IIR discutido aqui é dito ser biquad, uma vez que tem dois pólos e dois zeros, como ilustrado abaixo na Figura 2. A implementação do biquad é particularmente útil para implementações de pontos fixos, uma vez que os efeitos da quantização e estabilidade numérica são minimizados. No entanto, o sucesso global de qualquer implementação do biquad depende da precisão do número disponível, o que deve ser suficiente para garantir que os pólos quantificados estejam sempre dentro do círculo unitário.

  

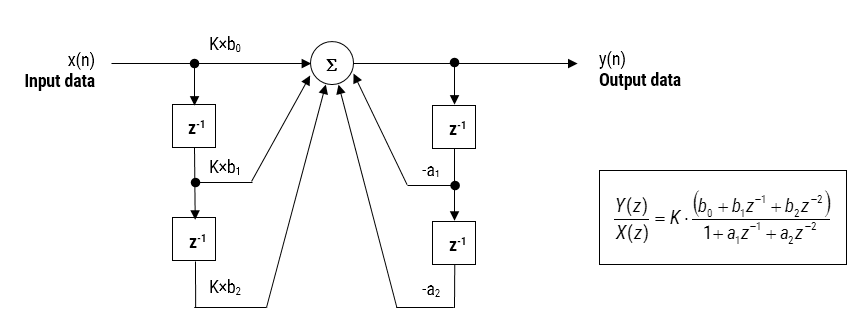
  Figura 2: função de realização e transferência do filtro de forma directa I (biquad).

  analisando a Figura 2, pode ver-se que a estrutura do biquad é na verdade composta por dois caminhos de feedback (escalados por \(\pequeno a_1\) e \(\pequeno a_2\)), três caminhos de alimentação para a frente (escalados por \(\pequeno b_0, b_1\) e \(\pequeno b_2\))) e um ganho de secção, \(\pequeno K\). Assim, a operação de filtragem da Figura 1 pode ser resumida pela seguinte equação recursiva simples::

  \(\displaystyle y(n)=K\times\Big – a_1 y(n-1)-a_2 y(n-2)\)

  Analisando a equação, observe que a biquad implementação requer apenas quatro adições (que requerem apenas um acumulador) e cinco multiplicações, o que pode ser facilmente acomodado em qualquer Cortex-M microcontrolador. O ganho de secção, \(\pequeno K\) também pode ser pré-multiplicado com os coeficientes do caminho anterior antes da implementação.

  uma coleção de filtros de Biquad é referida como uma cascata de Biquad, como ilustrado abaixo.

  

  o desenhador de filtros ASN pode projetar e implementar uma cascata de até 50 biquads (apenas edição profissional).

  ponto Flutuante de implementação

  Quando a implementação de um filtro em ponto flutuante (i.e. uso duplo ou individual aritmética de precisão) Forma Direta II estruturas são considerados para ser uma escolha melhor do que a Forma Direta I estrutura. A estrutura transposta de forma direta II é considerada a mais precisa numericamente para a implementação de vírgula flutuante, uma vez que os efeitos indesejáveis do amortecimento numérico são minimizados como visto pela análise das equações de diferença.

  

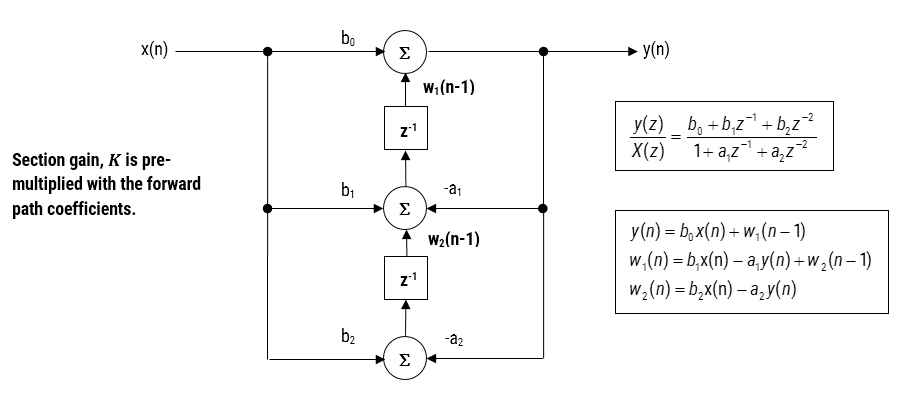
  Figura 3 – Forma Direta II Transposta strucutre, função de transferência e equações de diferenças

  O resumo de filtro (mostrado na Figura 4) fornece o designer com uma visão geral detalhada do filtro projetado, incluindo um resumo detalhado de especificações técnicas e o filtro de coeficientes, que apresenta de forma simples e rápida rota para documentar seu projeto.

  

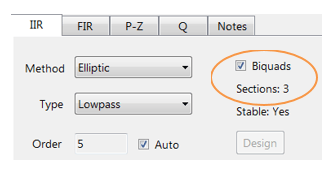
  o desenhador de filtros ASN suporta o desenho e implementação de filtros IIR de secção única e Biquad (configuração padrão).

  

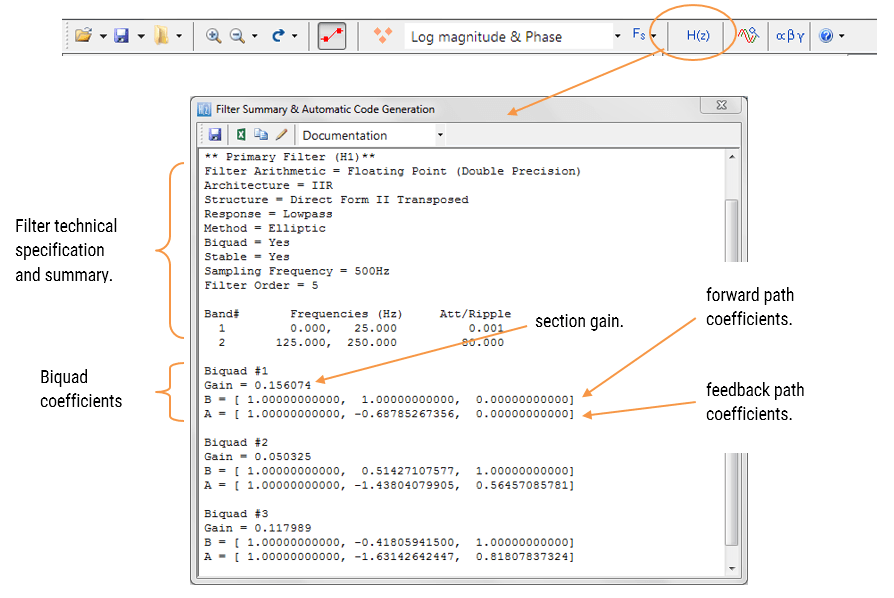
  Figura 4: Especificação pormenorizada.

  FIR definição

  Retornando o IIR linear constante coeficiente de diferença de equação, i.e.

  \(\displaystyle
  y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
  \)

  Observe que, quando damos o \(\small a_k\) coeficientes (i.e. o feedback) para zero, a definição reduz a nossa original do filtro FIR definição, o que significa que a FIR cálculo baseia-se apenas no passado e no presente de entradas de valores, a saber,:

  \(\displaystyle
  y(n)=\sum_{k=0}^{q}b_kx(n-k)
  \)

  Implementação

  Apesar de várias práticas de implementações de Abetos existir, a forma direta de estrutura e de sua transposta primo são, talvez, o mais comumente utilizado, e, como tal, todos projetados filtro de coeficientes de são destinados para a implementação de uma forma Direta estrutura.

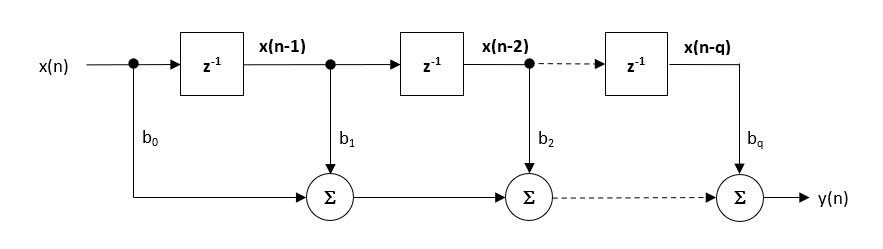
  a estrutura da forma direta e a equação de diferença associada são mostradas abaixo. A forma direta é defendida para a implementação do ponto fixo em virtude do conceito de acumulador único.

  \(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)

  

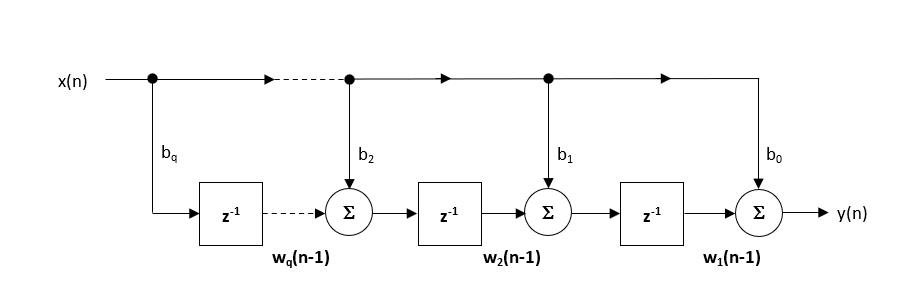
  a estrutura recomendada (padrão) dentro do Desenhador de filtros ASN é a estrutura transposta de forma direta, uma vez que isso oferece precisão numérica superior ao usar aritmética de ponto flutuante. Isto pode ser facilmente visto através da análise das equações de diferença abaixo (usadas para implementação), como os efeitos indesejáveis de amortecimento numérico são minimizados, uma vez que a adição de ponto flutuante é realizada em números de magnitude semelhante.

  \(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)

  

  o Que aprendemos?Os filtros digitais estão divididos nas duas categorias seguintes ::

  • Infinito resposta ao impulso (IIR)
  • Finite impulse response (FIR)

  IIR (infinite impulse response) filtros são geralmente escolhidos para aplicações onde a fase linear não é muito importante e a memória é limitada. Eles têm sido amplamente utilizados na equalização do som, biomédica, processamento de sinal do sensor, IoT/IIoT sensores inteligentes e de alta velocidade de telecomunicações/aplicações de RF.Filtros FIR (resposta de impulso finito) são geralmente escolhidos para aplicações onde a fase linear é importante e uma quantidade decente de memória e desempenho computacional estão disponíveis. Eles têm uma ampla implantação em aplicações de áudio e melhoria de sinal biomédico.

  ASN Filter Designer fornece aos engenheiros tudo o que eles precisam para projetar, experimentar e implantar filtros digitais complexos IIR e FIR para uma variedade de aplicações de medição de sensores. Estas vantagens, juntamente com a documentação automática e funcionalidade de geração de código, permitem aos engenheiros projetar e validar um filtro digital IIR/FIR em minutos e não em horas.