O Sistema Solar: a terra e a lua
os planetas estão distantes de nós a dezenas e centenas de milhões de quilômetros. Para evitar a utilização de números tão grandes se adota como unidade de distância a unidade astronômica (UA), Ou seja, a distância média entre a terra e o Sol, 149.600.000 km.a luz demora para cobrir esta distância 8 minutos e 19 segundos.
o tamanho do Sistema Solar ultrapassa a órbita de Plutão situado a 40 UA e é definido como aquele em que a força de atração do Sol se iguala à força de atração das estrelas mais próximas de nós. As dimensões do sistema Solar seriam então da ordem de 1,5 105 UA. Evidentemente, estas dimensões são muito pequenas comparadas com as dimensões da galáxia ou do Universo visível. As unidades que se tomam para medir essas enormes distâncias são o ano-luz e o parsec que equivale a 206 265 UA ou bem, a 3,26 anos-luz.
os planetas do Sistema Solar são divididos em dois grupos: o grupo terrestre formado por Mercúrio, Vênus, Terra e Marte e o grupo dos planetas gigantes formado por Júpiter, Saturno, Urano e Netuno.
todos os planetas, exceto Vênus e mercúrio, têm satélites, a maioria dos quais pertence aos planetas gigantes. A Terra, Júpiter, Saturno e Netuno têm os maiores satélites: a Lua, os satélites de Júpiter descobertos por Galileu (Io, Europa, Ganimedes, Calisto), o satélite Titã de Saturno e Tritão de Netuno.
os asteroides ocupam uma vasta região anular situada entre as órbitas de Marte e Júpiter, a uma distância média de 2,75 UA do Sol. O maior asteróide é Ceres que tem um diâmetro de 1000 km.
os cometas, foram catalogados cerca de 600, dividem-se em dois grupos, de período curto (menor de 20 anos) e de período longo (maior de 20 anos). Existem várias hipóteses sobre a origem dos cometas, incluindo a do astrônomo holandês J. Oort.
além dos corpos citados no espaço interplanetário, existe grande quantidade de partículas de tamanhos diferentes, predominando aquelas que têm uma massa de milésimos ou milionésimos de grama, que se denominam poeira meteórica. A formação destas partículas deve-se provavelmente ao choque de corpos maiores (asteroides) e à sua fragmentação sucessiva ao longo da existência e evolução do Sistema Solar.
a poeira meteórica é devida ao fenômeno da luz zodiacal, que é observado após o anoitecer ou antes do amanhecer, devido à dispersão da luz por essas partículas de poeira. A maioria das partículas evapora ao entrar na atmosfera terrestre (a alturas entre 80 e 120 km), apenas uma pequena proporção chega à superfície terrestre.
vejamos agora alguns dados relativos aos planetas do Sistema Solar
primeiro do Sol
| corpo celeste | raio | massa |
|---|---|---|
| Sol | 6.96 * 108 m | 1.98 * 1030 kg |
então, da Terra
| corpo celeste | semi-eixo maior | período | massa |
|---|---|---|---|
| Terra | 149.6 * 109 m | 1 ano=365.26 dias | 5.98 * 1024 kg |
e do resto dos planetas
| Planeta | semi-eixo maior (UA) | excentricidade | período (anos) | massa |
|---|---|---|---|---|
| mercúrio | 0.387 | 0.206 | 0.24 | 0.06 |
| Vênus | 0.723 | 0.007 | 0.62 | 0.82 |
| Terra | 1.000 | 0.017 | 1.00 | 1.00 |
| Marte | 1.524 | 0.093 | 1.88 | 0.11 |
| Júpiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturno | 9.539 | 0.056 | 29.46 | 95.1 |
| Urano | 19.182 | 0.047 | 84.01 | 14.6 |
| Netuno | 30.058 | 0.009 | 164.8 | 17.2 |
dados complementares são fornecidos na tabela a seguir:
- a inclinação do plano da órbita do planeta em relação à eclíptica (plano da órbita da Terra)
- período de rotação em torno de seu eixo. Tem sido muito complicado medir essa magnitude para planetas como mercúrio e Vênus. Os envelopes gasosos de Júpiter, Saturno, Urano e Netuno possuem a propriedade da rotação diferencial, ou seja, seus períodos de rotação varia de acordo com a latitude.
- a inclinação do eixo de rotação em relação ao plano da órbita. No caso de Vênus é de 177 equivale o que equivale a dizer que a inclinação do eixo é de 3 pero mas o sentido da rotação é inverso. O mesmo argumento vale para Urano, indicando que o eixo de rotação de Urano está quase no plano de sua órbita.
| Planeta | inclinação da órbita | período de rotação | Densidade g/cm3 | raio equatorial (km) | inclinação do eixo | n satélites de satélites |
|---|---|---|---|---|---|---|
| mercúrio | 7º.0 | 58d.6 | 5.44 | 2 439 | <30º | 0 |
| Vênus | 3 3.4 | 243d | 5.24 | 6 051 | 177º | 0 |
| Terra | 0 | 23h.9 | 5.52 | 6 378 | 23º.5 | 1 |
| Marte | 1 1.8 | 24h.6 | 3.95 | 3 394 | 25º.2 | 2 |
| Júpiter | 1 1.3 | 9h.9 | 1.33 | 71 398 | 3º.1 | 16 |
| Saturno | 2º.5 | 10h.2 | 0.69 | 60 000 | 26º.4 | 17 |
| Urano | 0..8 | 10h.8 | 1.26 | 25 400 | 98º | 5 |
| Netuno | 1º.8 | 15h.8 | 1.67 | 24 750 | 29º | 2 |
satélites
finalmente, fornecemos alguns dados relativos aos principais satélites dos planetas. Júpiter e Saturno têm muitos satélites cujo tamanho é muito maior que os de Marte, mas só mencionamos aqueles que têm um tamanho similar ou maior que a nossa lua.
| Planeta | Satélites | Densidade g/cm3 | raio médio (km) | raio órbita (103 km) | período (dias) |
|---|---|---|---|---|---|
| Terra | lua | 3.33 | 1 738 | 384.4 | 27.32 |
| Marte | Fobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Júpiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganimedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturno | Titã | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Netuno | Tritão | 2 200 | 394.7 | 5.84 |
atividades
- Determinar a massa do planeta Júpiter a partir dos dados do raio e do período de revolução de um de seus satélites.
- Determinar o raio da órbita de um satélite do planeta Júpiter a partir da massa desse planeta e do período de revolução do satélite.
- Determinar a intensidade do campo gravitacional g Na superfície dos planetas e alguns satélites, a partir dos dados de sua massa m e seu raio R ou, de sua densidade y e de seu raio.
exemplo: determinar a massa do planeta Júpiter sabendo que o raio da órbita de Io é de 421 600 km e que seu período de revolução é de 1.769 dias. Dado: a constante G vale 6.67 * 10-11 Nm2 / kg2
exemplo: Calcular o raio da órbita do satélite Calisto sabendo que seu período de revolução é de 16.689 dias e a massa do planeta Júpiter é de 1.901 * 1027 kg. dado: a constante G vale 6.67 * 10-11 Nm2/kg2
g = G M R 2 = 4 GP 3 GpR
dado: a constante G vale 6.67 * 10-11 Nm2 / kg2
a lua
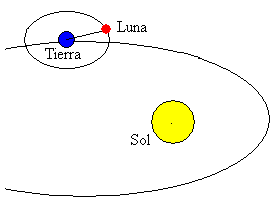
a Lua é um dos maiores corpos do sistema Solar. Sua órbita é quase circular (excentricidade ε=0,05) e o plano de sua órbita é inclinado 5 respecto em relação ao plano da órbita da Terra.
a distância média entre o centro da terra e a Lua é de 384.400 km. seu período de rotação ao redor da Terra é de 27.322 dias. A mudança da posição da Lua em relação ao Sol dá origem às fases da lua.
a Lua sempre apresenta a mesma face ao observador terrestre, devido ao efeito das forças de maré que a Terra exerce sobre a lua. O que significa que coincide o período de rotação da Lua em torno de seu eixo e o tempo que leva para completar uma órbita ao redor da Terra.
a Lua é o objeto celeste que mais fascinou a espécie humana. A antiga União Soviética Enviou pela primeira vez uma nave automática que pousou na superfície da Lua em 1959. Em 20 de julho de 1969, Neil Armstrong acompanhado por Edwin Aldrin foram os primeiros homens a caminhar sobre a superfície da lua no âmbito da missão Apollo 11. A última visita dos astronautas americanos à Lua ocorreu em 1972.
a origem da lua parece incerta, existem várias teorias:
-
que se formou ao mesmo tempo que a terra com o material proveniente de uma nebulosa
-
que um corpo celeste se dividiu em duas partes dando origem à terra e à Lua
-
que a Lua se formou em outro lugar e foi capturada pela Terra
-
que a Terra colidiu com um objeto celeste de grande tamanho (do tamanho de Marte ou maior) e que a Lua se formou com o material ejetado dessa colisão.
a última teoria parece, por enquanto, a mais aceita pela comunidade científica.
trajetória da lua
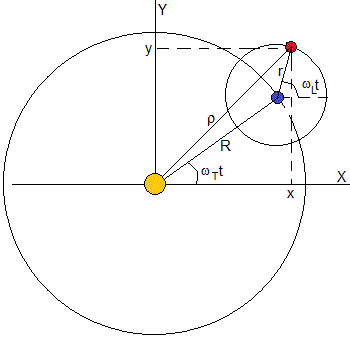
considere um planeta e seu satélite. O planeta descreve uma órbita circular de raio R em torno de sua estrela com velocidade angular constante wT = 2 PT / PT, sendo PT O período ou tempo que trada em dar uma volta completa. O satélite descreve uma órbita circular coplanaria de raio r com velocidade angular constante wL=2π/PL, sendo PL o período de tempo que leva para dar uma volta completa
A posição do satélite em relação a um sistema de referência cuja origem é a estrela, é
x=Rcos( ω T )+rcos( ω L t ) e=Rsin( ω T )+rsin( ω L t )
Seja α=wT/wL
{ x=Rcos( α ω L t )+rcos( ω L t ) e=Rsin( α ω L t )+rsin( ω L t ) { x=Rcos( α 2π P L t )+rcos( 2π P L t ) e=Rsin( α 2π P L t )+rsin( 2π P L t )
Chamemos τ=t/PL
x R =cos( α·2πτ )+ r R cos( 2πτ ) e R =sin( α·2πτ )+ r R sin( 2πτ )
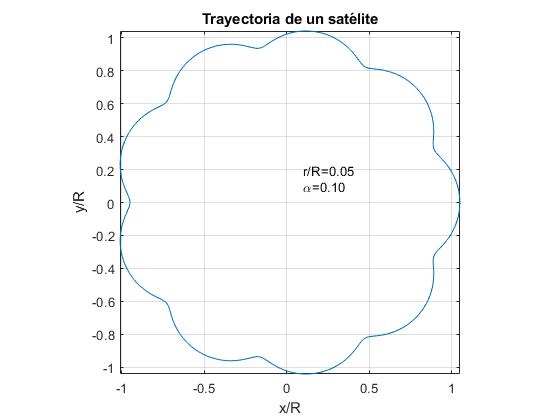
Representamos a trajetória de um satélite para α=0.1 e para três valores do quociente r/R.
- r/R<α. Exemplo, r / R = 0,05
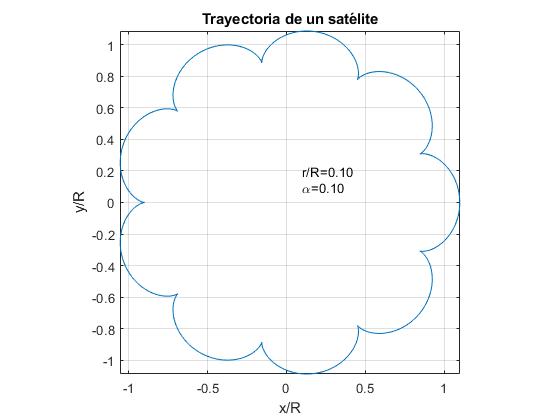
- r/r=α. Exemplo, r / r = 0.1
- r/r> α. Exemplo, r / r=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
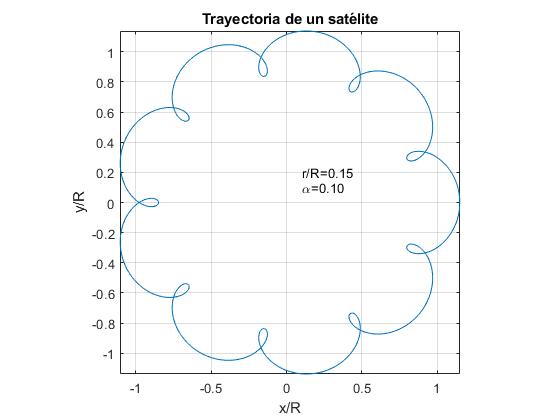
Para o caso da terra e da Lua, os dados são:
- raio da órbita da lua: R=384.4 * 106 m, período PL = 27.32 d
- raio da órbita da Terra: R = 149,6 * 109 m, período PT=365,26 d
α=wT/wL=PL/PT=0,0748. r / R = 0,0026
a órbita da lua será semelhante à primeira figura. Na representação gráfica da trajetória da Lua para estes valores de α e r/R não apreciam-se as oscilações da distância radial entre o Sol e a Lua
Aceleração da Lua
A distância ρ desde o Sol à Lua é
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T )t )
Calculamos as componentes retangulares de aceleração
{ dx dt =− ω T Rsin( ω T )− ω L rsin( ω L t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L t ) { x = d 2 x d t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L t ) a e = d 2 e d t 2 =− ω T 2 Rsin( ω T )− ω L 2 rsin( ω L t )
A componente radial da aceleração
a ρ = a → · ρ → ρ = a x x+ y e x 2 + y 2 =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rrcos( ( ω L − ω T )t ) R 2 + r 2 +2rR cos( ( ω L − ω T )t )
Os valores mínimo e máximo são obtidos quando cos((wL-wT)t)=±1
a máx =− ω T 2 R 2 + ω L 2 r 2 +( ω T 2 + ω L 2 )Rr R 2 + r 2 +2rR =−( ω T 2 R+ ω L 2 r ) a mín =− ω T 2 R 2 + ω L 2 r 2 −( ω T 2 + ω L 2 )Rr R 2 + r 2 −2rR =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
a Lua é o único satélite do Sistema Solar, cujo componente radial da aceleração é negativo, diz-se que ‘a lua cai em direção ao Sol’
as fases da lua
a figura mostra a Lua em diferentes posições de sua órbita ao redor da Terra. O Sol está muito distante iluminando ambos os corpos celestes (na parte superior da figura)
metade da Lua é iluminada pelo Sol (na cor branca) e metade da lua mais próxima da Terra é visível pelo observador terrestre. À medida que a Lua se move ao redor da Terra, vemos diferentes frações da parte iluminada pelo Sol (as zonas na cor amarela).
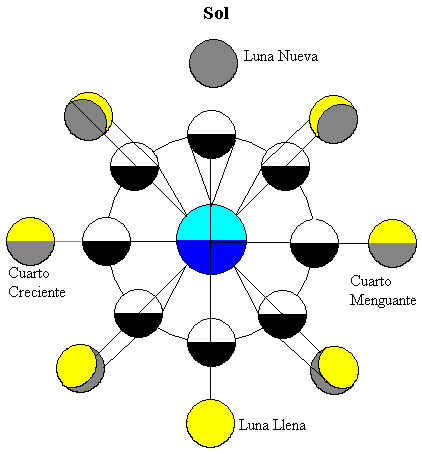
-
quando a Lua está entre a terra e o Sol, a parte da lua mais próxima da terra está escura, então não podemos ver a lua, essa fase é chamada de lua nova.
-
quando a terra está entre o Sol e a Lua, a parte da lua mais próxima da Terra é a metade iluminada, esta fase é chamada de lua cheia.
-
quando a Lua está em posições intermediárias, apenas metade da parte mais próxima da Terra é iluminada. Portanto, vemos apenas um quarto da lua, essas duas fases são chamadas de quartos, crescente ou minguante, dependendo se a parte iluminada que é visível da Terra tende a crescer ou diminuir.
Nota: Este programa interativo tenta explicar as fases da Lua, mas não é uma representação fiel da órbita da lua, que forma um ângulo de 5º com o plano da eclíptica (da órbita da terra ao redor do Sol), nem da orientação do eixo da Terra que forma aproximadamente 23º com a normal ao plano da eclíptica.
foi desenhada uma linha vermelha que atravessa a Lua para que o leitor aprecie a coincidência do período de rotação da Lua em torno de seu eixo e o tempo que leva para completar uma órbita ao redor da terra e, portanto, a Lua apresenta sempre a mesma face à Terra.
Eclipses da lua
os eclipses da lua ocorrem sempre que a Lua está em fase cheia e sempre que o Sol, a terra e a Lua estão em linha reta. Então a Lua está na sombra produzida pela terra, como mostrado na figura.
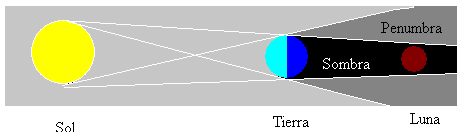
existem outros tipos de eclipse lunar, que dependem do alinhamento dos três corpos celestes. A lua pode se encontrar em zona não iluminada (sombra) ou parcialmente iluminada (penumbra).
o eclipse Solar ocorre quando a Lua se interpõe entre o Sol e a terra, a Lua está em fase Nova. A Lua é 400 vezes menor que o Sol, mas a Lua está 400 vezes mais próxima da Terra, portanto, o tamanho aparente de ambos os corpos vistos da Terra é quase o mesmo. A Lua Pode, desta maneira, produzir um eclipse total do Sol, se for observado na zona de sombra projetada pela Lua sobre a Terra.
dados da lua
| Massa (kg) | 7.349·1022 |
| raio (km) | 1737. 4 |
| densidade média (g / cm3) | 3.34 |
| Distância Média à Terra (km) | 384 000 |
| período orbital (dias) | 27.32166 |
| aceleração da gravidade no Equador (m / s2) | 1.62 |
| excentricidade da órbita | 0.0549 |
| inclinação da órbita (graus) | 5.1454 |
-
Calcule o raio da órbita circular da Lua ao redor da Terra sabendo que o período É 27,32 dias. Calcule também a velocidade da lua. Dados: G =6,67 * 10-11 Nm2 / kg2, a massa da Terra é M=5,98 * 1024 kg.
-
Calcule a aceleração da gravidade g na superfície da lua.
-
Calcule o quociente entre o diâmetro do Sol e o diâmetro da lua. Calcule a relação entre a distância média entre o Sol e a terra e a Lua e a Terra. Dados: raio do Sol 6.96 * 108 m, Distância Média Terra-Sol 1.49·1011 m
-
Calcule a posição do centro de massa do sistema Terra-Lua, medido a partir do centro da Terra.
-
Calcule a força de atração da terra sobre a lua, compare-a com a força de atração do Sol sobre a lua. Dado: massa do Sol, 1.98 * 1030 kg
referências
M. Márov. Planetas do Sistema Solar. Editora Mir.
Saiba mais sobre os planetas em Cuántos quantos planetas existem no nosso Sistema Solar?. ComofuncionaQue.com
para a seção ‘trajetória da lua’
David C. Johnston. Cycloidal paths in physics as superpositions of translational and rotational motions. Am. J. Phys.87 (10), October 2019, pp. 808-810
The Moon Always Veers Toward The Sun. Páginas de matemática.