Um círculo é dividido uniformemente em seis triângulos iguais
Hi Marilynn,
em primeiro lugar, vou dizer – lhe as minhas suposições sobre como é a sua imagem:
- cada triângulo tem um vértice (canto) no centro do círculo
- cada triângulo tem cantos na circunferência do círculo (assim, dois lados de cada triângulo é um raio)
- os triângulos compartilham lados (não há paisagens entre triângulos)
a imagem geral parece uma flor – cada triângulo é uma pétala.

a área desconhecida é o que fica em torno do exterior do círculo, entre a circunferência e o lado exterior de cada triângulo. Esta área desconhecida é dividida em seis seções congruentes (iguais em todos os sentidos – como os triângulos são “iguais” em todos os sentidos – incluindo área, comprimento de lado e comprimento de arco). Não é claro se você quer dizer que a área de um arco é Pi (não na verdade split Pie, embora pronouced o mesmo), ou todas as seis seções tomadas em conjunto é Pi. A seguir, parto do princípio de que uma das secções externas tem uma área de Pi, de modo que a área de todas as seis secções consideradas em conjunto é 6 vezes Pi. Precisamos de encontrar o raio do círculo, chamar-lhe r.
também vou usar P para representar Pi (ou Aprox. 3.14). Há muita informação que podemos tirar dos triângulos.:
- os ângulos no centro são todos 60 graus. Isto é porque os seis ângulos no centro são todos iguais, e um círculo tem 360 graus. Assim como 360 numerados por 6.Cada triângulo é isósceles. Isto porque dois lados são iguais (os lados que são um raio).
- cada triângulo é, de facto, equilátero. Porque é iscoceles, os dois ângulos externos também são iguais. Mas há 180 graus em um triângulo, 60 já são usados no ângulo central, deixando 180-60=120 graus para os ângulos externos. Mas, 120 divididos por 2 é 60 graus, então todos os três ângulos são iguais, então é isóscles.
- cada lado em cada triângulo é de comprimento R. Isto porque temos 6 triângulos congruentes (“iguais” em todos os sentidos) equiláteros, e porque dois lados de cada triângulo é um raio.
da geometria dos triângulos, precisamos fazer alguma álgebra. Porque conhecemos uma área, e precisamos de um raio, precisamos de uma fórmula (ou equação) para raio em termos de área (no que se segue, manter o objetivo de uma fórmula em mente). A área do círculo é P*r2 (R2 significa R ao quadrado, e * significa multiplicar) a área das seções sobras fora dos triângulos, mas dentro do círculo (uma área que já não deve ser 6*P), também pode ser encontrada subtraindo a área dos triângulos da área do círculo. Temos de encontrar uma área de um dos triângulos equiláteros.
Método 1 para calcular uma área de um triângulo
a área de um triângulo é b*h/2 Isto é onde alguma trigonometria é necessária: desenhar uma linha de um vértice para um lado oposto que divide o lado oposto ao meio e está em ângulos retos. Isto divide o triângulo equilátero em dois triângulos congruentes de ângulo direito, e o novo lado é a altura, chamá – lo h. precisamos encontrar h.
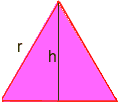
usando trig em um dos triângulos de ângulo direito, temos sin60 = h / R mas sin60 = SQR (3) / 2, onde sqr(3) significa a raiz quadrada de três so sqr(3)/2 = h/r multiplique ambos os lados por R para obter h = r*sqr (3)/2 R agora, a área de um triângulo equilátero é b*h/2 = (r)*(r * sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(p-6*sqr (3)/4)) usar a ordem de operações para calcular em uma calculadora (com P=3.14): r= 5.896… Então, o raio do círculo é de aprox. 5.9. Paul