Bootstrap în R

Bootstrap este o metodă de inferență despre o populație folosind date eșantion.Bradley Efron a introdus-o pentru prima dată în acest senshârtie în 1979.Bootstrap se bazează pe eșantionare cu înlocuire din datele eșantionului. Această tehnică poate fi utilizată pentru a estima eroarea standard a oricărei statistici și pentru aobține un interval de încredere (CI) pentru aceasta. Bootstrap este deosebit de utilcând CI nu are o formă închisă sau are una foarte complicată.

să presupunem că avem un eșantion de n elemente:X = {x1, x2, …, xn} și suntem interesați de CI pentru unele statistici T = T(X). Bootstrapframework este simplă. Repetăm doar r ori următorulschema: pentru repetarea i-a, eșantion cu înlocuire n elemente din proba disponibilă (unele dintre ele vor fi culese de mai multe ori). Apel thisnew eșantion i-lea eșantion bootstrap, Xi, și statistica calculatedesired Ti = T (Xi).

ca rezultat, vom obține valorile R ale statisticii noastre:T1, T2, …, TR. Le numimrealizările Bootstrap ale lui T sau o distribuție bootstrap a lui T. Pe baza acestuia, putem calcula CI pentru T. Există mai multe modalități de a face acest lucru. Luarea percentilelor pare a fi cea mai ușoară.

Bootstrap în acțiune

să folosim (încă o dată) binecunoscutul set de date iris. Aruncati o privire la un firstfew rânduri:

să presupunem că vrem să găsim CIs pentru medianSepal.Length, median Sepal.Width și coeficientul de corelație rang Spearman între thesetwo. Vom folosi R ‘ s boot pachet și o funcție numită… boot. Pentru a-i folosi puterea, trebuie să creăm o funcție care calculează statisticile noastre din datele reeșantionate. Ar trebui să aibă cel puțin două argumente: un dataset și un vector care conține indices de elemente dintr-un set de date care au fost selectate pentru a crea un eșantion bootstrap.

dacă dorim să calculăm CIs pentru mai multe statistici simultan, funcția noastră trebuie să le returneze ca un singur vector.

pentru exemplul nostru, poate arăta astfel:

library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}

foo alege elementele dorite (care numere sunt stocate în indices) din data și calculează coeficientul de corelație al primelor două coloane(method='s' este folosit pentru a alege coeficientul de rang al lui Spearman,method='p' va rezulta cu coeficientul lui Pearson) și medianele lor.

putem adăuga și câteva argumente suplimentare, de ex. permiteți utilizatorului să aleagă tipul coeficient de corelație odcorrelation:

foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}

pentru a face acest tutorial mai general, voi folosi ultima versiune a foo.

acum, putem folosi funcția boot. Trebuie să-i furnizăm un nume oddataset, funcția pe care tocmai am creat-o, Numărul de repetări (R)și orice argumente suplimentare ale funcției noastre (cum ar fi cor.type). Mai jos, Iuse set.seed pentru reproductibilitatea acestui exemplu.

set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot funcția returnează un obiect al clasei numit… (da, ai dreptate!)boot. Are două elemente interesante. $t conține valorile R ale statisticii noastre generate de procedura bootstrap (realizările bootstrap ofT):

$t0 conține valori ale statisticilor noastre în setul de date original, complet:

myBootstrap$t0## -0.1667777 5.8000000 3.0000000

imprimarea boot obiect la consola oferă câteva informații suplimentare:

original este la fel ca $t0. bias este o diferență între media realizărilor Bootstrap (cele de la $t), numită estimare bootstrap de T și valoare în setul de date original (cel de la $t0).

colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000

std. error este o eroare standard a estimării bootstrap, care este egalădevierea standard a realizărilor bootstrap.

apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414

diferite tipuri de bootstrap CIs

înainte de a începe cu CI, merită întotdeauna să aruncăm o privire ladistribuția realizărilor bootstrap. Putem folosi plot funcție, cuindex spune la care dintre Statisticile calculate în foo dorim să ne uităm. Aici index=1 este coeficientul de corelație al unui Spearman între lungimea și lățimea sepalului, index=2este o lungime mediană od sepal șiindex=3 este o lățime mediană od sepal.

plot(myBootstrap, index=1)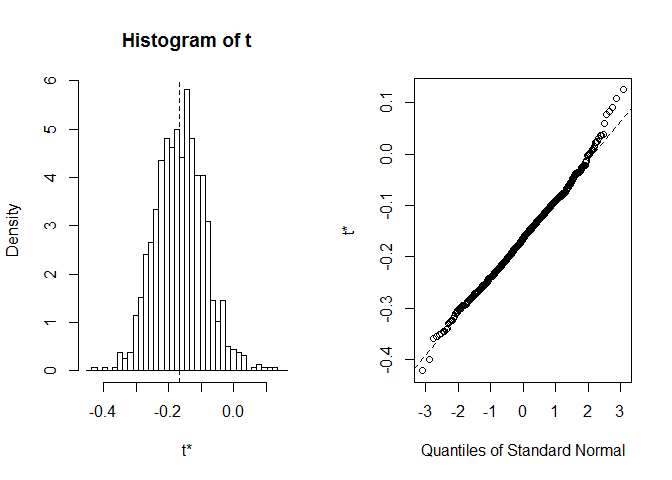

distribuția coeficienților de corelație bootstrap pare destulnormal. Să găsim CI pentru ea. Putem folosi boot.ci. Este implicit la95 % CIs, dar poate fi modificat cu parametrul conf.

boot.ci oferă 5 tipuri de Bootstrap CIs. Unul dintre ei, studentizedinterval, este unic. Este nevoie de o estimare a varianței bootstrap. Nu am furnizat-o, așa că R tipărește un avertisment:bootstrap variances needed for studentized intervals. Varianțăestimările pot fi obținute cu bootstrap de nivelul doi sau (mai ușor) cutehnica hackknife. Acest lucru este într-un fel dincolo de domeniul de aplicare al acestui tutorial,așa că să ne concentrăm pe restul de patru tipuri de Bootstrap CIs.

dacă nu vrem să le vedem pe toate, le putem alege pe cele relevante în Argumentul type. Valorile posibile sunt norm, basic, stud, perc, bca ora vectorului acestora.

funcția boot.ci creează obiectul clasei… (da, ați ghicit!)bootci. Elementele sale sunt numite la fel ca tipurile de CI utilizate în Argumentul type. $norm este un vector cu 3 elemente care conține nivel de încredereși limite CI.

boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc și $bca sunt vectori cu 5 elemente care conțin, de asemenea, percentile utilizate pentru a calcula CI (vom reveni la acest lucru mai târziu):

boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178

un pic de notație (Îmi pare rău!)

pentru a obține un sentiment de ce sunt diferite tipuri de CI, trebuie să introducemunele notații. Deci, să:

• t⋆ fi bootstrap estimare (de bootstraprealizations),
• t0 fi o valoare a statisticii în setului de date original,
• se⋆ fi o eroare standard de bootstrap estimare,
• b fie o prejudecată de bootstrap estimateb = t⋆ − t0
• α fi un nivel de încredere, de obicei α = 0.95,
• za fi o $1-\frac \alpha 2$-quantile de standardnormal de distribuție,
• va fi un α-a percentilă a distribuției de bootstraprealizations.

percentila ci

cu notația de mai sus, percentila CI este:

(θ(1 − α)/2, θ1 − (1 − α)/2)

deci, aceasta are doar relevante percentile. Nimic mai mult.

IÎ normală

un IÎ tipic pentru Wald ar fi:

t0⋆

dar, în cazul bootstrap, ar trebui să-l corecteze pentru părtinire. Deci, devine:

$$ t_0 – B \pm z_\alpha \cdot se^\star \\2t_0 – t^\star \pm z_\alpha \cdot se^\star$$

CI de bază

ci percentila nu este, în general, recomandată, deoarece funcționează slabcând vine vorba de distribuții cu coadă ciudată. CI de bază (numită și cipivotală sau empirică) este mult mai robustă în acest sens. Rationalebehind este de a calcula diferențele dintre fiecare replicationand bootstrap t0 și de a folosi percentilele distribuției lor. Fulldetails pot fi găsite, de exemplu, în L. Wasserman ‘ s All ofStatistics

formula finală pentru ci de bază este:

(2T0 − inkt1 – (1-inkt) / 2, 2T0-inkt(1-inkt)/2)

BCA CI

BCa provine de la bias-corectat, accelerat. Formulapentru că nu este foarte complicat, dar oarecum neintuitiv, așa că o voi sări peste.Vezi articolul lui Thomas J. DiCiccio și BradleyEfron dacă sunteți interesați de detalii.

accelerația menționată în numele metodei necesită utilizarea anumitor centile ale realizărilor bootstrap. Uneori se poate întâmpla astaacestea ar fi unele percentile extreme, eventual valori aberante.BCa poate fi instabilă în astfel de cazuri.

să ne uităm la BCA CI pentru mediana lățimii petalei. Inoriginal set de date, această mediană este egală cu exact 3.

obținem IÎ BCa (2,9; 2,9). Ciudat, dar din fericire Rne-a avertizat că extreme order statistics used as endpoints. Să vedem ce sa întâmplat exact aici:

plot(myBootstrap, index=3)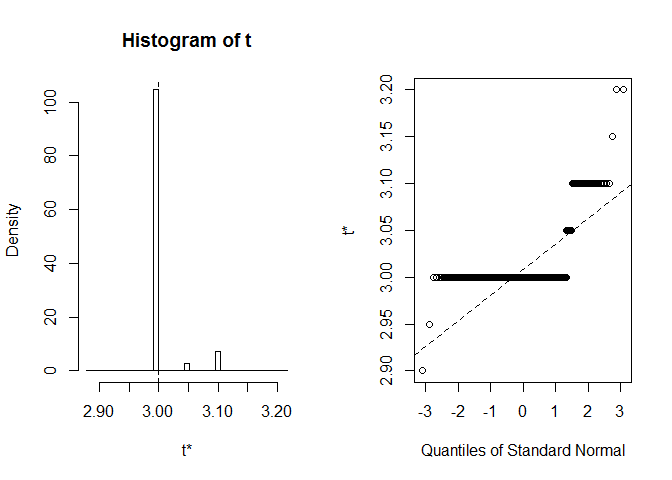

distribuția realizărilor bootstrap este neobișnuită. Marea majoritate a acestora (peste 90%) sunt 3s.

table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2

replicarea rezultatelor

uneori, avem nevoie pentru a recrea replicări bootstrap. Dacă putem folosi R pentru aceasta, aceasta nu este o problemă. set.seed funcția rezolvă problema.Recrearea replicărilor bootstrap în alte programe software ar fi mult mai complicată. Mai mult, pentru R mare, recalcularea în R nu poate fi, de asemenea, o opțiune (din cauza lipsei de timp, de exemplu).

putem rezolva această problemă, salvând indicii elementelor originaldataset, care au format fiecare eșantion bootstrap. Aceasta este ceea ce face funcția boot.array(cu argumentul indices=T).

tableOfIndices<-boot.array(myBootstrap, indices=T)

fiecare rând este un eșantion bootstrap. Eg., primul nostru eșantion conține următoarele elemente:

Setare indices=F (implicit), vom primi un răspuns la întrebarea „cumde multe ori fiecare element al setului de date original a apărut în fiecare bootstrapeșantion?”. De exemplu, în primul eșantion: a apărut elementul 1 al setului de datecând, elementul 2 nu a apărut deloc, elementul 3 a apărut o dată, al 4-lea de două ori și așa mai departe.

un tabel ca acesta ne permite să recreăm realizarea bootstrap în afara R.Sau în R în sine atunci când nu vrem să folosim set.seed și să facem din nou toate calculele.

onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

să verificăm dacă rezultatele sunt aceleași:

Da, sunt!

dacă doriți să aflați mai multe despre învățarea automată în R, urmați cursul DataCamp Machine Learning Toolbox.