diferența dintre filtrele IIR și FIR: un ghid practic de proiectare
un filtru digital este un algoritm matematic care funcționează pe un set de date digitale (de exemplu, datele senzorilor) pentru a extrage informații de interes și a elimina orice informație nedorită. Aplicațiile acestui tip de tehnologie includ eliminarea erorilor din datele senzorilor sau chiar curățarea zgomotului pe un semnal măsurat pentru o analiză mai ușoară a datelor. Dar cum alegem cel mai bun tip de filtru digital pentru aplicația noastră? Și care sunt diferențele dintre un filtru IIR și un filtru FIR?
filtrele digitale sunt împărțite în următoarele două categorii:
- răspuns la impuls infinit (IIR)
- răspuns la impuls finit (FIR)
după cum sugerează și numele, fiecare tip de filtru este clasificat după lungimea răspunsului său la impuls. Cu toate acestea, înainte de a începe cu o analiză matematică detaliată, este prudent să apreciem diferențele de performanță și caracteristici ale fiecărui tip de filtru.
exemplu
pentru a ilustra diferențele dintre un FIR IIR și un FIR de ordinul 14 (linie solidă) și un Chebyshev de ordinul 4 de tipul I IIR (linie punctată) este prezentat mai jos în Figura 1. Observați că, deși spectrele de magnitudine au un grad similar de atenuare, spectrul de fază al filtrului IIR este neliniar în banda de trecere (\(\small 0\rightarrow7.5Hz\)) și devine foarte neliniar la frecvența de întrerupere, \(\small f_c=7,5 Hz\). De asemenea, observați că FIR necesită un număr mai mare de coeficienți (15 vs IIR 10) pentru a se potrivi cu caracteristicile de atenuare ale IIR.
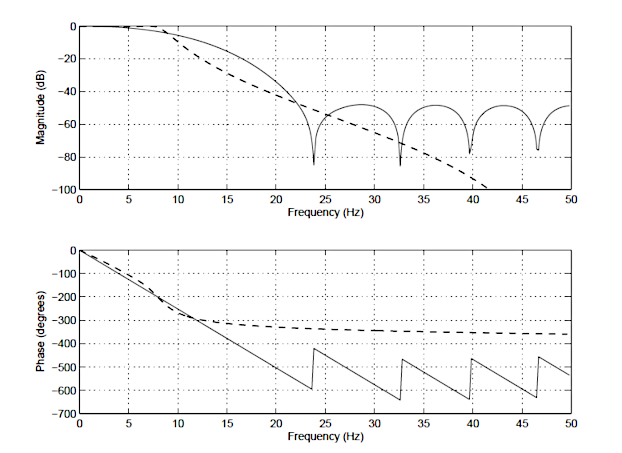
acestea sunt doar câteva dintre diferențele dintre cele două tipuri de filtre. Va urma acum un rezumat detaliat al principalelor avantaje și dezavantaje ale fiecărui tip de filtru.
filtre IIR
filtrele IIR (infinite impulse response) sunt în general alese pentru aplicații în care faza liniară nu este prea importantă și memoria este limitată. Acestea au fost utilizate pe scară largă în egalizarea audio, procesarea semnalului senzorilor biomedic, senzorii inteligenți IoT/IIoT și aplicațiile de telecomunicații/RF de mare viteză.
avantaje
- costuri reduse de implementare: necesită mai puțini coeficienți și memorie decât filtrele FIR pentru a satisface un set similar de specificații, adică frecvența de întrerupere și atenuarea benzii de oprire.
- latență scăzută: potrivit pentru control în timp real și aplicații RF de mare viteză în virtutea numărului redus de coeficienți.
- echivalent analogic: poate fi utilizat pentru imitarea caracteristicilor filtrelor analogice folosind transformările de cartografiere a planului s-Z.
dezavantaje
- caracteristici de fază neliniare: Caracterele de fază ale unui filtru IIR sunt în general neliniare, în special în apropierea frecvențelor de întrerupere. Filtrele de egalizare All-pass pot fi utilizate pentru a îmbunătăți caracteristicile fazei benzii de trecere.
- analiză mai detaliată: necesită mai multă scalare și analiză numerică de depășire atunci când este implementată în punct fix. Structura filtrului direct form II este deosebit de sensibilă la efectele cuantizării și necesită o atenție deosebită în timpul fazei de proiectare.
- stabilitate numerică: Mai puțin stabile numeric decât omologii lor FIR (răspuns la impuls finit), datorită căilor de feedback.
filtre FIR
filtre FIR (răspuns la impuls finit) sunt în general alese pentru aplicații în care faza liniară este importantă și sunt disponibile o cantitate decentă de memorie și performanțe computaționale. Ei au o largă implementat în audio și Biomedicale semnal enhancement aplicații. Structura lor complet zero (discutată mai jos) asigură că nu devin niciodată instabile pentru niciun tip de semnal de intrare, ceea ce le oferă un avantaj distinct față de IIR.
avantaje
- fază liniară: brazii pot fi proiectați cu ușurință pentru a avea fază liniară. Aceasta înseamnă că nu este introdusă nicio distorsiune de fază în semnalul care trebuie filtrat, deoarece toate frecvențele sunt deplasate în timp cu aceeași cantitate – menținându-și astfel relațiile armonice relative (adică grup constant și întârziere de fază). Acest lucru nu este cu siguranță cazul filtrelor IIR, care au o caracteristică de fază neliniară.
- stabilitate: deoarece brazii nu folosesc valori de ieșire anterioare pentru a calcula ieșirea lor actuală, adică. nu au feedback, nu pot deveni niciodată instabili pentru niciun tip de semnal de intrare, ceea ce le oferă un avantaj distinct față de filtrele IIR.
- răspuns în frecvență arbitrar: funcția Firarb() a Parks-McClellan și ASN FilterScript permit proiectarea unui FIR cu un răspuns de magnitudine arbitrar. Aceasta înseamnă că un FIR poate fi personalizat mai ușor decât un IIR.
- performanța punctului fix: efectele cuantizării sunt mai puțin severe decât cele ale unui IIR.
dezavantaje
- cerințe de calcul și memorie ridicate: Brazii necesită de obicei mult mai mulți coeficienți pentru a obține o întrerupere bruscă decât omologii lor IIR. Consecința acestui fapt este că necesită mult mai multă memorie și o cantitate semnificativ mai mare de operații MAC (multiple și acumulate). Cu toate acestea, arhitecturile moderne de microcontrolere bazate pe nucleele Cortex-M ale Arm includ acum suport hardware DSP prin SIMD (instrucțiuni de semnal, date multiple) care accelerează semnificativ operația de filtrare.
- latență mai mare: numărul mai mare de coeficienți înseamnă că, în general, un FIR este mai puțin potrivit decât un IIR pentru aplicații rapide de mare viteză. Acest lucru devine problematic pentru aplicațiile de control în buclă închisă în timp real, unde un filtru FIR poate avea prea multă întârziere de grup pentru a obține stabilitatea buclei.
- fără echivalent analogic: folosind transformarea Z biliniară, potrivită (maparea s-z), un filtru analogic poate fi ușor transformat într-un filtru IIR echivalent. Cu toate acestea, acest lucru nu este posibil pentru un FIR, deoarece nu are echivalent analogic.
definiții matematice
după cum s-a discutat în introducere, numele IIR și FIR provin din definițiile matematice ale fiecărui tip de filtru, adică un filtru IIR este clasificat după răspunsul său teoretic la impuls infinit,
y(n)=\sum_{k=0}^{\infty}h(k)x (n-k)
\)
și un FIR clasificat după răspunsul său de impuls finit,
y (n)=\sum_{k=0}^{N-1}h (k)x (n-k)
\)
vom analiza acum proprietățile matematice ale fiecărui tip de filtru la rândul său.
definiție IIR
după cum s-a văzut mai sus, un filtru IIR este clasificat după răspunsul său teoretic la impuls infinit,
\(\displaystyle y (n)=\sum_{k = 0}^{\infty}h(k) x(n-k)\)
practic vorbind, nu este posibil să se calculeze ieșirea unui IIR folosind această ecuație. Prin urmare, ecuația poate fi rescrisă în termenii unui număr finit de poli \(\mic p\) și zerouri \(\mic q\), așa cum este definit de ecuația liniară a diferenței de coeficient constant dată de:
y (n)= \ sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky (n-k)
\)
unde, \(\small a_k\) și \(\small b_k\) sunt coeficienții polinomiali ai numitorului și numărătorului filtrului, ale căror rădăcini sunt egale cu polii și respectiv zerourile filtrului. Astfel, o relație între ecuația diferenței și transformarea z (Funcția de transfer) poate fi definită prin utilizarea proprietății de întârziere a transformării z astfel încât,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- k}}{1+ \ sum \ limits_{k=1}^p a_kz^{- k}}
\)
după cum se vede, funcția de transfer este o reprezentare a domeniului de frecvență al filtrului. Observați, de asemenea, că polii acționează asupra datelor de ieșire, iar zerourile asupra datelor de intrare. Deoarece polii acționează asupra datelor de ieșire și afectează stabilitatea, este esențial ca razele lor să rămână în interiorul cercului unității (adică <1) Pentru BIBO (intrare mărginită, ieșire mărginită) stabilitate. Razele zerourilor sunt mai puțin critice, deoarece nu afectează stabilitatea filtrului. Acesta este motivul principal pentru care filtrele FIR (răspuns la impuls finit) sunt întotdeauna stabile.
BIBO stability
un sistem liniar invariant în timp (LTI) (cum ar fi un filtru digital) se spune că este intrare mărginită, ieșire mărginită stabilă sau BIBO stabilă, dacă fiecare intrare mărginită dă naștere unei ieșiri mărginite, ca
\(\displaystyle \sum_{k=0}^{\infty}\stânga|h(k)\dreapta|<\infty \)
unde, \(\mic h(k)\) este răspunsul la impuls al sistemului LTI. Analizând această ecuație, ar trebui să fie clar că criteriul de stabilitate BIBO va fi satisfăcut numai dacă polii sistemului se află în interiorul cercului unității, deoarece Roc (regiunea de convergență) a sistemului trebuie să includă cercul unității. În consecință, este suficient să spunem că un semnal de intrare delimitat va produce întotdeauna un semnal de ieșire delimitat dacă toți polii se află în interiorul cercului unității.
zerourile, pe de altă parte, nu sunt constrânse de această cerință și, în consecință, se pot afla oriunde pe planul z, deoarece nu afectează în mod direct stabilitatea sistemului. Prin urmare, o analiză a stabilității sistemului poate fi efectuată calculând mai întâi rădăcinile funcției de transfer (adică rădăcinile polinoamelor numărătorului și numitorului) și apoi trasând polii și zerourile corespunzătoare pe planul Z.
o situație interesantă apare dacă există poli pe cercul unității, deoarece se spune că sistemul este marginal stabil, deoarece nu este nici stabil, nici instabil. Deși sistemele marginal stabile nu sunt BIBO stabile, acestea au fost exploatate de proiectanții de oscilatoare digitale, deoarece răspunsul lor la impuls oferă o metodă simplă de generare a undelor sinusoidale, care s-au dovedit a fi de neprețuit în domeniul telecomunicațiilor.
filtre Biquad IIR
se spune că implementarea filtrului IIR discutată aici este biquad, deoarece are doi poli și două zerouri așa cum este ilustrat mai jos în Figura 2. Implementarea biquad este deosebit de utilă pentru implementări cu punct fix, deoarece efectele cuantizării și stabilității numerice sunt reduse la minimum. Cu toate acestea, succesul general al oricărei implementări biquad depinde de precizia numărului disponibil, care trebuie să fie suficientă pentru a se asigura că polii cuantificați sunt întotdeauna în interiorul cercului unității.
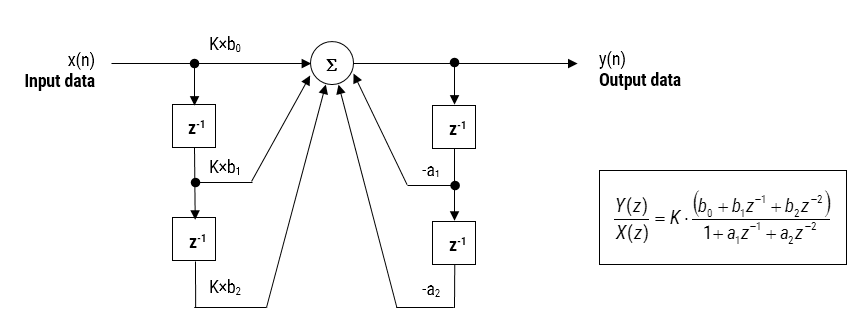
Figura 2: Forma directă i (biquad) funcția de realizare și transfer a filtrului IIR.
analizând Figura 2, se poate observa că structura biquad este de fapt compusă din două căi de feedback (scalate de \(\small a_1\) și \(\small A_2\)), trei căi de avans (scalate de \(\small b_0, b_1\) și \(\small b_2\)) și un câștig de secțiune, \(\small K\). Astfel, operația de filtrare din Figura 1 poate fi rezumată prin următoarea ecuație recursivă simplă:
\(\displaystyle y (n)=K \ ori \ Mare-A_1 y (n-1) – a_2 y (n-2)\)
analizând ecuația, observați că implementarea biquad necesită doar patru adăugiri (necesitând un singur acumulator) și cinci înmulțiri, care pot fi ușor găzduite pe orice microcontroler Cortex-M. Câștigul secțiunii, \(\mic K\) poate fi, de asemenea, pre-înmulțit cu coeficienții de cale înainte înainte de implementare.
o colecție de filtre Biquad este denumită cascadă Biquad, așa cum este ilustrat mai jos.

designerul de filtre ASN poate proiecta și implementa o cascadă de până la 50 de biquad-uri (numai ediția profesională).
implementare în virgulă mobilă
atunci când se implementează un filtru în virgulă mobilă (adică folosind aritmetică de precizie dublă sau unică) structurile directe de forma II sunt considerate a fi o alegere mai bună decât structura directă de forma I. Forma directă ii structura transpusă este considerată cea mai precisă din punct de vedere numeric pentru implementarea în virgulă mobilă, deoarece efectele nedorite ale tamponării numerice sunt reduse la minimum, așa cum se vede prin analizarea ecuațiilor de diferență.
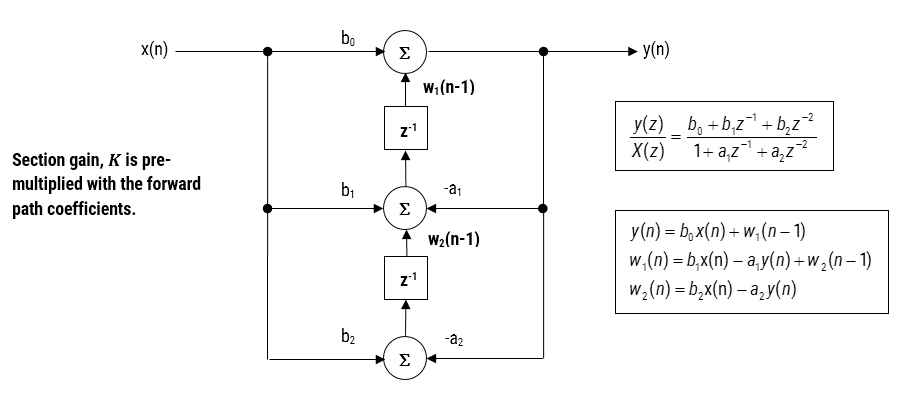
Figura 3-Direct Form II transpuse strucutre, funcția de transfer și ecuațiile de diferență
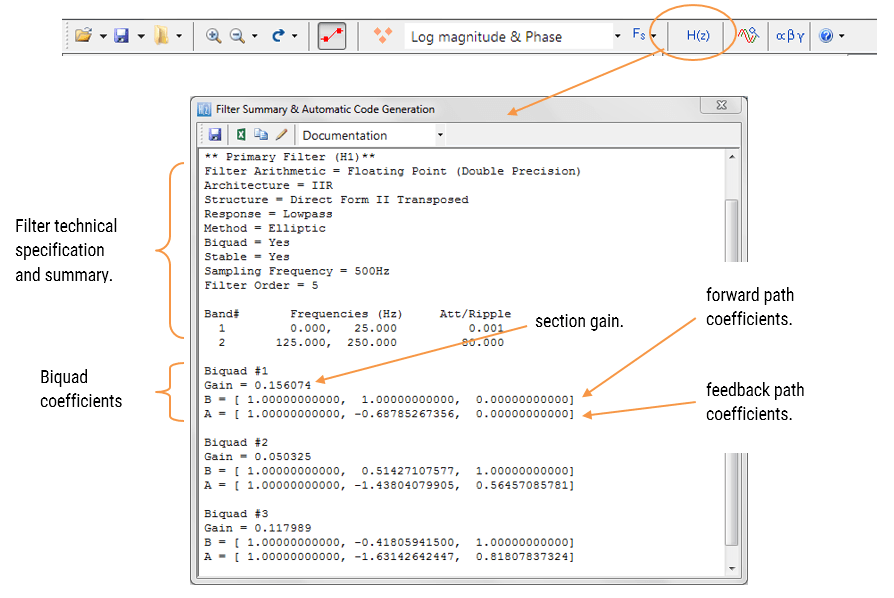
rezumatul filtrului (prezentat în Figura 4) oferă proiectantului o prezentare detaliată a filtrului proiectat, inclusiv un rezumat detaliat al specificațiilor tehnice și al coeficienților filtrului, care prezintă o cale rapidă și simplă de documentare a designului dvs.
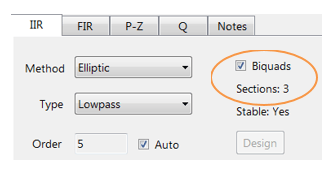
proiectantul filtru ASN sprijină proiectarea și punerea în aplicare a atât singură secțiune și Biquad (setare implicită) filtre IIR.
FIR definition
returnând ecuația de diferență a coeficientului constant liniar al IIR, adică
y(n)=\sum_{k=0}^{q}b_kx (n-k)-\sum_{k = 1}^{p}a_ky(n-k)
\)
observați că atunci când setăm coeficienții \(\small a_k\) (adică feedback-ul) la zero, definiția reduce la originalul nostru definiția filtrului FIR, ceea ce înseamnă că calculul FIR se bazează doar pe valorile intrărilor trecute și prezente, și anume:
y (n) = \ sum_{k = 0}^{q}b_kx (n-k)
\)
implementare
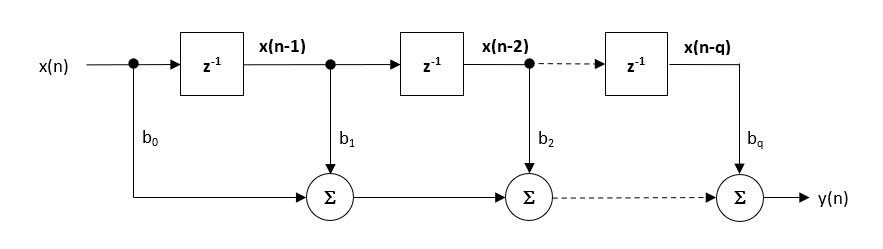
deși există mai multe implementări practice pentru fir, structura de formă directă și vărul său transpus sunt probabil cele mai frecvent utilizate și, ca atare, toți coeficienții de filtrare proiectați sunt destinați implementării într-o structură de formă directă.
structura formei directe și ecuația diferenței asociate sunt prezentate mai jos. Forma directă este susținută pentru implementarea punctului fix în virtutea conceptului de acumulator unic.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x (n-2) + …. +b_qx (n-q) \)
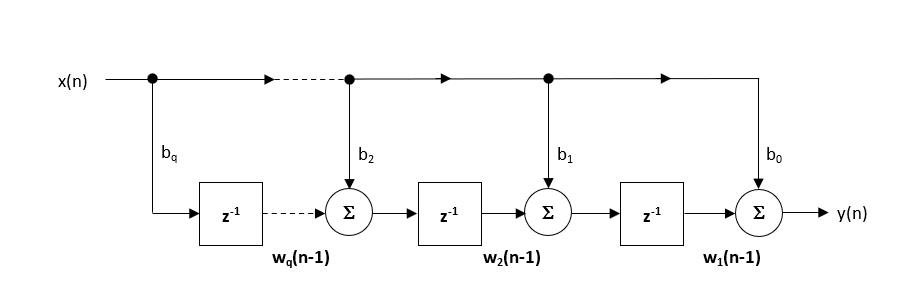
structura recomandată (implicită) în cadrul proiectantului filtrului ASN este structura transpusă în formă directă, deoarece aceasta oferă o precizie numerică superioară atunci când se utilizează aritmetica în virgulă mobilă. Acest lucru poate fi văzut cu ușurință prin analizarea ecuațiilor de diferență de mai jos (utilizate pentru implementare), deoarece efectele nedorite ale tamponării numerice sunt reduse la minimum, deoarece adăugarea în virgulă mobilă se efectuează pe numere de magnitudine similară.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{nyrkkinainti}\)
ce am învățat?
filtrele digitale sunt împărțite în următoarele două categorii:
- răspuns la impuls infinit (IIR)
- răspuns la impuls finit (FIR)
filtrele IIR (infinite impulse response) sunt în general alese pentru aplicații în care faza liniară nu este prea importantă și memoria este limitată. Acestea au fost utilizate pe scară largă în egalizarea audio, procesarea semnalului senzorilor biomedic, senzorii inteligenți IoT/IIoT și aplicațiile de telecomunicații/RF de mare viteză.
filtrele FIR (răspuns la impuls finit) sunt în general alese pentru aplicații în care faza liniară este importantă și sunt disponibile o cantitate decentă de memorie și performanțe computaționale. Ei au o largă implementat în audio și Biomedicale semnal enhancement aplicații.
ASN Filter Designer oferă inginerilor tot ce au nevoie pentru a proiecta, experimenta și implementa filtre digitale complexe IIR și FIR pentru o varietate de aplicații de măsurare a senzorilor. Aceste avantaje, împreună cu documentația automată și funcționalitatea de generare a codului, permit inginerilor să proiecteze și să valideze un filtru digital IIR/FIR în câteva minute, mai degrabă decât în ore.
