Un cerc este împărțit uniform în șase triunghiuri egale
bună Marilynn,
în primul rând, vă voi spune presupunerile mele despre cum arată imaginea dvs:
- fiecare triunghi are un vârf (colț) în centrul cercului
- fiecare triunghi are colțuri pe circumferința cercului (deci, două laturi ale fiecărui triunghi este o rază)
- triunghiurile împart laturile (nu există gape între triunghiuri)
imaginea de ansamblu arată ca o floare – fiecare triunghi este o petală.

zona necunoscută este ceea ce rămâne în jurul exteriorului cercului, între circumferință și partea exterioară a fiecărui triunghi. Această zonă necunoscută este împărțită în șase secțiuni congruente (egale în toate privințele – așa cum triunghiurile sunt „egale” în toate privințele – inclusiv aria, lungimea laturii și lungimea arcului). Nu este clar dacă vrei să spui zona de un arc este Pi (nu de fapt divizat plăcintă, deși pronouced la fel), sau toate cele șase secțiuni luate împreună este Pi. În cele ce urmează, voi presupune că una dintre secțiunile exterioare are o suprafață de Pi, astfel încât aria tuturor celor șase secțiuni luate împreună este de 6 ori Pi. Trebuie să găsim raza cercului, să o numim r.
voi folosi și P pentru a sta pentru Pi (sau aprox. 3.14). Acum, există o mulțime de informații pe care le putem garnisi din triunghiuri:
- unghiurile din centru sunt toate de 60 de grade. Acest lucru se datorează faptului că cele șase unghiuri din centru sunt toate egale, iar un cerc are 360 de grade. Deci, face 360 edivided de 6.
- fiecare triunghi este izoscel. Acest lucru se datorează faptului că două laturi sunt egale (laturile care sunt o rază).
- fiecare triunghi, este de fapt echilateral. Deoarece este iscoceles, cele două unghiuri exterioare sunt, de asemenea, egale. Dar există 180 de grade într-un triunghi, 60 sunt deja utilizate în unghiul central, lăsând 180-60=120 de grade pentru unghiurile exterioare. Dar, 120 împărțit la 2 este de 60 de grade, deci toate cele trei unghiuri sunt egale, deci este izoscle.
- fiecare latură a fiecărui triunghi are lungimea r. Acest lucru se datorează faptului că avem 6 triunghiuri echilaterale congruente („egale” în toate privințele) și pentru că două laturi ale fiecărui triunghi sunt o rază.
din geometria triunghiurilor, trebuie să facem niște algebră. Deoarece cunoaștem o zonă și avem nevoie de o rază, avem nevoie de o formulă (sau ecuație) pentru rază în termeni de zonă (în cele ce urmează, țineți cont de obiectivul unei formule). Aria cercului este P * r2 (R2 înseamnă R pătrat și * înseamnă înmulțire) aria secțiunilor rămase în afara triunghiurilor, dar în interiorul cercului (o zonă pe care deja nu trebuie să fie 6*P), poate fi găsită și scăzând aria triunghiurilor din zona cercului. Trebuie să găsim o zonă a unuia dintre triunghiurile echilaterale.
Metoda 1 pentru calcularea unei arii a unui triunghi
aria unui triunghi este b*h/2 Aici este nevoie de o anumită trigonometrie: desenați o linie de la un vârf la o parte opusă care împarte partea opusă în jumătate și este în unghi drept. Aceasta împarte triunghiul echilateral în două triunghiuri congruente în unghi drept, iar noua latură este înălțimea, numiți-o h. trebuie să găsim h.
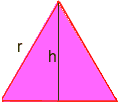
folosind trig într-unul dintre triunghiurile unghiulare drepte, avem sin60 = h / r, dar sin60 = sqr(3)/2, Unde sqr(3) înseamnă rădăcina pătrată a trei deci sqr(3)/2 = h/r înmulțiți ambele părți cu r pentru a obține h = r*sqr(3)/2 R acum, aria unui triunghi echilateral este B*h/2 = (r)*(r*sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6 * sqr(3)/4)) Utilizați ordinea operațiunilor pentru a calcula pe un calculator (cu P=3.14): r= 5.896… Deci, raza cercului este de aprox. 5.9. Pavel