utilizarea logaritmilor în lumea reală

logaritmii sunt peste tot. Ați folosit vreodată următoarele fraze?

• 6 cifre
• cifre duble
• ordin de mărime
• rata dobânzii

descrieți numerele în termeni de puteri de 10, un logaritm. Și o rată a dobânzii este logaritmul creșterii unei investiții.

surprins de faptul că logaritmii sunt atât de comune? Și eu. Cele mai multe încercări de Matematică din lumea reală (TM) evidențiază logaritmii într-o formulă arcană sau pretind că suntem geologi fascinați de scara Richter. „Oamenilor de știință le pasă de bușteni și ar trebui și tu. De asemenea, vă puteți imagina o lume fără zinc?”

nu, nu, nu, nu, nu, nu, nu! (Mama mia!)

matematica exprimă concepte cu notație precum „ln” sau „jurnal”. Găsirea „matematicii în lumea reală” înseamnă a întâlni idei în viață și a vedea cum ar putea fi scrise cu notație. Nu căutați simbolurile literale! Când a fost ultima dată când ai scris un semn de divizie? Când a fost ultima dată când ai tăiat niște mâncare?

Ok, OK, înțelegem: despre ce sunt logaritmii?

logaritmii găsesc cauza unui efect, adică intrarea pentru o anumită ieșire

un „efect” obișnuit este să vezi ceva crescând, cum ar fi trecerea de la \100$la \150$în 5 ani. Cum s-a întâmplat asta? Nu suntem siguri, dar logaritmul găsește o posibilă cauză: o revenire continuă a ln(150/100) / 5 = 8,1% ar reprezenta această schimbare. S-ar putea să nu fie cauza reală (s-a întâmplat toată creșterea în ultimul an?), dar este o medie lină pe care o putem compara cu alte modificări.

apropo, noțiunea de „cauză și efect” este nuanțată. De ce este 1000 mai mare decât 100?

• 100 este 10 care a crescut de la sine pentru 2 perioade de timp ($10 * 10$)
• 1000 este 10 care a crescut de la sine pentru 3 perioade de timp ($10 * 10 * 10$)

ne putem gândi la numere ca ieșiri (1000 este „1000 ieșiri”) și intrări („de câte ori trebuie să crească 10 pentru a face aceste ieșiri?”). Deci,

1000 outputs > 100 outputs

deoarece

3 inputs > 2 inputs

sau cu alte cuvinte:

log(1000) > log(100)

de ce este util acest lucru?

logaritmii pun numerele la o scară prietenoasă cu oamenii.

un număr mare ne rupe creierul. Milioane și trilioane sunt „foarte mari”, chiar dacă un milion de secunde înseamnă 12 zile și un trilion de secunde înseamnă 30.000 de ani. Este diferența dintre un an de vacanță American și întreaga civilizație umană.

trucul pentru a depăși „orbirea numărului imens” este de a scrie numere în termeni de „intrări” (adică baza lor de putere 10). Această scară mai mică (de la 0 la 100) este mult mai ușor de înțeles:

• puterea 0 = $10^0$ = 1 (un singur element)
• puterea 1 = $10^1$ = 10
• puterea de 3 = $10^3$ = mii
• puterea de 6 = $10^6$ = milioane
• puterea de 9 = $10^9$ = miliarde
• puterea de 12 = $10^12$ = trilioane
• puterea de 23 = $10^23$ = numărul de molecule într-o duzină de grame de carbon
• puterea de 80 = $10^80$ = Numărul de molecule din univers

o scară de la 0 la 80 ne-a dus de la un singur element la numărul de lucruri din univers. Nu prea ponosit.

logaritmii numără înmulțirea ca pași

logaritmii descriu modificările în ceea ce privește înmulțirea: în exemplele de mai sus, fiecare pas este de 10 ori mai mare. Cu jurnalul natural, fiecare pas este” e ” (2.71828…) ori mai mult.

când se ocupă de o serie de multiplicări, logaritmii ajută la „numărarea” acestora, la fel cum adăugarea contează pentru noi atunci când se adaugă efecte.

arată-mi matematica

timpul pentru carne: să vedem unde apar logaritmii!

salariu de șase cifre sau cheltuieli de 2 cifre

descriem numerele în termeni de cifre, adică. câte puteri de 10 au (sunt în zeci, sute, mii, zece mii etc.). Adăugarea unei cifre înseamnă” înmulțirea cu 10″, adică.

logaritmii numără numărul de înmulțiri adăugate, deci începând cu 1 (o singură cifră) adăugăm încă 5 cifre (10 $^5$) și 100.000 obțin un rezultat de 6 cifre. Vorbind despre ” 6 „în loc de” o sută de mii ” este esența logaritmilor. Acesta oferă un sentiment dur de scară, fără a sări în detalii.

întrebare Bonus: cum ați descrie 500.000? A spune „6 cifre” este înșelător, deoarece 6 cifre implică adesea ceva mai aproape de 100.000. Ar funcționa” figura 6.5″?

nu chiar. În capul nostru, 6.5 înseamnă” la jumătatea drumului ” între 6 și 7 cifre, dar aceasta este mentalitatea unui adder. Cu logaritmi a”.5 ” înseamnă jumătate din punct de vedere al multiplicării, adică rădăcina pătrată ($9^.5 $ înseamnă că rădăcina pătrată a lui 9 — 3 este la jumătatea drumului în ceea ce privește înmulțirea, deoarece este de la 1 la 3 și de la 3 la 9).

luând Jurnalul (500.000) obținem 5,7, adăugăm 1 pentru cifra suplimentară și putem spune „500.000 este un 6.7 Numărul figura”. Încercați-l aici:

ordinul de mărime

noi geeks place această frază. Înseamnă aproximativ „diferență de 10x”, dar sună mai rece decât”1 cifră mai mare”.

în computere, unde totul este numărat cu biți (1 sau 0), fiecare bit are un efect de dublare (nu 10x). Deci, trecerea de la 8 la 16 biți este „8 ordine de mărime” sau $2^8 = 256$ ori mai mare. („Mai mare” în acest caz se referă la cantitatea de memorie care poate fi abordată.) Mergând de la 16 la 32 de biți înseamnă un plus de 16 ordine de mărime, sau $2^16$ ~ 65,536 ori mai multă memorie care pot fi abordate.

ratele dobânzilor

cum ne dăm seama ratele de creștere? O țară nu intenționează să crească la 8,56% pe an. Priviți PIB-ul pe un an și PIB-ul pe Următorul, și luați logaritmul pentru a găsi rata de creștere implicită.

cele două interpretări preferate ale logaritmului natural(ln (x)), adică jurnalul natural al 1.5:

• presupunând o creștere de 100%, cât timp trebuie să crești pentru a ajunge la 1,5? (.405, mai puțin de jumătate din perioada de timp)
• presupunând 1 unitate de timp, cât de repede trebuie să crești pentru a ajunge la 1,5? (40.5% pe an, compus continuu)

logaritmii sunt modul în care ne dăm seama cât de repede creștem.

scara de măsurare: Google PageRank

Google dă fiecare pagină de pe web un scor (PageRank), care este o măsură aproximativă de autoritate / importanță. Aceasta este o scară logaritmică, care în capul meu înseamnă „PageRank numără numărul de cifre din scorul dvs.”.

deci, un site cu pagerank 2 („2 cifre”) este de 10 ori mai popular decât un site PageRank 1. Site-ul meu este PageRank 5 și CNN are PageRank 9, deci există o diferență de 4 ordine de mărime ($10^4$ = 10,000).

aproximativ vorbind, primesc aproximativ 7000 de vizite / zi. Folosind matematica mea plic, pot ghici CNN devine despre 7000 * 10.000 = 70 milioane de vizite / zi. (Cum am făcut asta? În capul meu, cred că $7k * 10k = 70 * k * k = 70 * m$). S-ar putea să aibă de câteva ori mai mult decât atât (100m, 200m), dar probabil nu până la 700m.

Google transmite o mulțime de informații cu o scară foarte dură (1-10).

scara de măsurare: Richter, decibeli, etc.

suspin. Suntem la exemplul tipic „logaritmilor din lumea reală”: Scara Richter și Decibel. Ideea este de a pune evenimente care pot varia drastic (cutremure) pe o singură scară cu un interval mic (de obicei 1 la 10). La fel ca PageRank, fiecare creștere de 1 punct este o îmbunătățire de 10 ori a puterii. Cel mai mare cutremur înregistrat de oameni a fost de 9,5; impactul Peninsulei Yucat, care a făcut probabil dispariția dinozaurilor, a fost de 13.

decibelii sunt similari, deși pot fi negativi. Sunetele pot merge de la intens liniștit (pindrop) la extrem de tare (avion) și creierul nostru poate procesa Totul. În realitate, sunetul motorului unui avion este de milioane (miliarde, trilioane) de ori mai puternic decât un pindrop și este incomod să ai o scară care merge de la 1 la un gazillion. Jurnalele păstrează totul la o scară rezonabilă.

grafice logaritmice

veți vedea adesea elemente reprezentate grafic pe o „scară jurnal”. În capul meu, aceasta înseamnă că o parte numără „numărul de cifre” sau „numărul de înmulțiri”, nu valoarea în sine. Din nou, acest lucru ajută la afișarea evenimentelor care variază sălbatic pe o singură scară (mergând de la 1 la 10, nu de la 1 la miliarde).

legea lui Moore este un exemplu excelent: dublăm numărul de tranzistori la fiecare 18 luni (mulțumim Wikipedia pentru imagine).

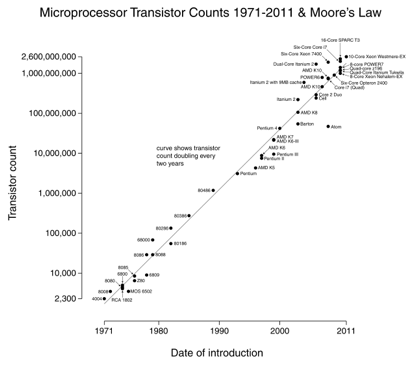
lucru elegant despre grafice log-scară este modificări exponențiale (viteza procesorului) apar ca o linie dreaptă. Creșterea 10x pe an înseamnă că sunteți în mod constant marș în sus scara „cifre”.

înainte și în sus

dacă un concept este bine cunoscut, dar nu este bine iubit, înseamnă că trebuie să ne construim intuiția. Găsiți analogiile care funcționează și nu vă mulțumiți cu panta pe care o va face un manual. În capul meu:

• logaritmii găsesc cauza principală a unui efect (a se vedea creșterea, găsiți rata dobânzii)
• ajută la numărarea înmulțirilor sau cifrelor ,cu bonusul numărului parțial (500k este un număr de 6,7 cifre)

matematică fericită.

alte posturi din această serie

1. un ghid intuitiv pentru funcțiile exponențiale & e
2. demistificarea logaritmului Natural (ln)
3. un ghid vizual pentru ratele dobânzilor simple, compuse și continue
4. definiții comune ale e (Colorizat)
5. înțelegerea exponenților (de ce 0^0 = 1?)
6. utilizarea logaritmilor în lumea reală
7. cum să gândim cu exponenți și logaritmi
8. înțelegerea creșterii Discrete vs. continue
9. ce înseamnă cu adevărat un exponent?
10. Î: De ce este e special? (2.718…, nu 2, 3,7 sau alt număr?)