Skjult Markov-Model: enkel Definition & oversigt

Statistikdefinitioner >

den skjulte Markov-Model (HMM) er en relativt enkel måde at modellere sekventielle data på. En skjult Markov-model indebærer, at Markov-modellen, der ligger til grund for dataene, er skjult eller ukendt for dig. Mere specifikt kender du kun observationsdata og ikke oplysninger om staterne. Med andre ord er der en bestemt type model, der producerer dataene (en Markov-Model), men du ved ikke, hvilke processer der producerer dem. Du bruger dybest set din viden om Markov-modeller til at gøre et veluddannet gæt om modelens struktur.

Hvad er en Markov-Model?

for at afdække den skjulte Markov-Model skal du først forstå, hvad en Markov-Model er i første omgang. Her opretter jeg et simpelt eksempel ved hjælp af to ting, der er meget velkendte i Sandsynlighed: terninger og poser med farvede bolde.

modelkomponenterne, som du vil bruge til at oprette den tilfældige model, er:

• en seks-sidet rød dør.
• en ti-sidet sort dør.
• en rød taske med ti bolde. Ni bolde er røde, den ene er sort.
• en sort taske med tyve bolde. En bold er rød, nitten er sorte.

“sort” og ” rød ” er de to tilstande i denne model (med andre ord, du kan være sort, eller du kan være rød).
Opret nu modellen ved at følge disse trin:

1. EMISSIONSTRIN: rul en matrice. Bemærk det nummer, der kommer op. Dette er emissionen. I ovenstående grafik valgte jeg en rød matrice til at starte (vilkårlig — jeg kunne have valgt sort) og rullet 2.
2. overgangstrin: vælg tilfældigt en bold fra posen med den farve, der matcher den matrice, du rullede i trin 1. Jeg rullede en rød dør, så jeg skal vælge en bold fra den røde taske. Jeg trak en sort bold ud, så jeg går over til den sorte dør for den næste emission.

du kan derefter gentage disse trin til et vist antal emissioner. For eksempel kan gentagelse af denne sekvens af trin 10 gange give dig Sættet {2,3,6,1,1,4,5,3,4,1}. Processen med overgang fra en stat til den næste kaldes en Markov-proces.

overgang fra rød til sort eller sort til rød bærer forskellige sandsynligheder, da der er forskellige antal sorte og røde kugler i poserne. Følgende diagram viser sandsynlighederne for denne særlige model, som har to tilstande (sort og rød):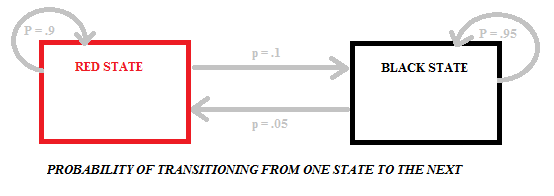

Hidden Markov Model Notation

List = (A,B,List), er stenografi notation for en HMM. Anden notation bruges i skjulte Markov-modeller:

• a = tilstandsovergangssandsynlighed (aij)
• B = observationssandsynlighedsmatrice (bj(k))
• N = antal tilstande i modellen {1,2…N} eller tilstanden på tidspunktet t-kur st
• M = antal forskellige observationssymboler pr .tilstand
• K = {spørgsmål 0, spørgsmål 1,. . . , kn−1} = Forskellige tilstande af Markov-processen
• T = længde af observationssekvensen
• V = {0, 1, . . . , M − 1} = sæt af mulige observationer
• O = (O0, o1, . . . , OT -1) = observationssekvens
• liter = initial tilstandsfordeling (ni)
• s = tilstandssekvens (s1, s2… sn)
• HK = skjult tilstand
• HK = observation.

tre grundlæggende problemer

tre grundlæggende problemer kan løses med skjulte Markov modeller:

1. i betragtning af den skjulte Markov-Model prit = (A, B, prit) og en sekvens af observationer O, find sandsynligheden for en observation P(o | prit). Dette kaldes undertiden Evalueringsproblemet.
2. i betragtning af den skjulte Markov-Model larr = (A, B, larr) og en observationssekvens O, find den mest sandsynlige tilstandssekvens (s1, s2… SN). Dette kaldes undertiden et Afkodningsproblem.
3. Find en observationssekvens (O1, O2…på og skjult Markov-Model ris = (A, B, ris), der maksimerer sandsynligheden for O. Dette kaldes undertiden et læringsproblem eller optimeringsproblem.

Rabiner, L. R.” En tutorial om skjulte Markov-modeller og udvalgte applikationer inden for talegenkendelse”, Proceedings of the IEEE, vol.77, s.257-286, Feb. 1989.
Stempel, M. (2013). En afslørende Introduktion til skjulte Markov-modeller. Hentet 8/6/2013 fra: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

brug for hjælp til et hjemmearbejde eller test spørgsmål? Med Chegg Study kan du få trinvise løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg tutor er gratis!