Solsystemet: jorden og Månen
planeterne er titusinder og hundreder af millioner kilometer væk fra os. For at undgå brugen af så store tal vedtages den astronomiske enhed (AU) som afstandsenheden, det vil sige den gennemsnitlige afstand mellem Jorden og solen, 149.600.000 km.Lys tager 8 minutter og 19 sekunder at dække denne afstand.
Solsystemets størrelse overstiger Plutos bane ved 40 AU og er defineret som en, hvor solens tiltrækningskraft er lig med tiltrækningskraften for stjernerne tættest på os. Solsystemets dimensioner ville så være i størrelsesordenen 1, 5 105 AU. Det er klart, at disse dimensioner er meget små sammenlignet med galaksens eller det synlige universs dimensioner. Enhederne, der er taget for at måle disse enorme afstande, er lysåret og parsec, der svarer til 206 265 AU eller 3, 26 lysår.
solsystemets planeter er opdelt i to grupper: den jordbaserede gruppe dannet af Merkur, Venus, Jorden og Mars og den kæmpe planetgruppe dannet af Jupiter, Saturn, Uranus og Neptun.
alle planeter undtagen Venus og Merkur har satellitter, hvoraf de fleste hører til de gigantiske planeter. Jorden, Jupiter, Saturn og Neptun har de største satellitter: Månen, Jupiters satellitter opdaget af Galileo (Io, Europa, Ganymedes, Callisto), satellitten Titan af Saturn og Triton af Neptun.
asteroider indtager en stor ringformet region mellem Mars og Jupiters kredsløb i en gennemsnitlig afstand på 2, 75 AU fra solen. Den største asteroide er Ceres, som har en diameter på 1000 km.
kometer, der er katalogiseret omkring 600, er opdelt i to grupper, kort periode (under 20 år) og lang periode (over 20 år). Der er flere hypoteser om kometernes oprindelse, herunder den hollandske astronom J. Oort.
ud over de organer, der er nævnt i det interplanetære rum, er der et stort antal partikler af forskellig størrelse, overvejende dem med en masse på tusindedele eller milliontedele af et gram, der kaldes meteorisk støv. Dannelsen af disse partikler skyldes sandsynligvis kollisionen mellem større kroppe (asteroider) og deres successive fragmentering gennem Solsystemets eksistens og udvikling.
meteorisk støv er ansvarlig for fænomenet stjernetegn, som observeres efter skumring eller før daggry på grund af spredning af lys af disse støvpartikler. De fleste partikler fordamper, når de kommer ind i Jordens atmosfære (i højder mellem 80 og 120 km), kun en lille del når jordens overflade.
lad os nu se på nogle data relateret til solsystemets planeter
solens første
| himmellegeme | Radio | masse |
|---|---|---|
| Søn | 6, 96·108 m | 1, 98 * 1030 kg |
derefter ud af landet
| himmellegeme | semi-hovedakse | periode | masse |
|---|---|---|---|
| jord | 149,6 * 109 m | 1 år=365,26 dage | 5.98 * 1024 kg |
og resten af planeterne
| Planet | halv-hovedakse (AU) | ekscentricitet | periode (år) | masse |
|---|---|---|---|---|
| kviksølv | 0.387 | 0.206 | 0.24 | 0.06 |
| Venus | 0.723 | 0.007 | 0.62 | 0.82 |
| jorden | 1.000 | 0.017 | 1.00 | 1.00 |
| Mars | 1.524 | 0.093 | 1.88 | 0.11 |
| Jupiter | 5.203 | 0.048 | 11.86 | 318 |
| Saturn | 9.539 | 0.056 | 29.46 | 95.1 |
| Uranus | 19.182 | 0.047 | 84.01 | 14.6 |
| Neptun | 30.058 | 0.009 | 164.8 | 17.2 |
i den følgende tabel er angivet som supplerende data:
- hældningen af planet for planetens kredsløb med hensyn til ekliptikken (planet for jordens kredsløb)
- rotationsperioden omkring sin akse. Det har været meget vanskeligt at måle denne størrelse for planeter som Merkur og Venus. De gasformige skaller af Jupiter, Saturn, Uranus og Neptun har egenskaben for differentiel rotation, det vil sige deres rotationsperioder varierer alt efter breddegrad.
- hældningen af rotationsaksen i forhold til kredsløbets plan. I tilfælde af Venus er det 177 kr, hvilket svarer til at sige, at aksens hældning er 3 kr, men rotationsretningen er omvendt. Det samme argument gælder for Uranus, hvilket indikerer, at Uranus rotationsakse næsten er i planet for dens bane.
| Planet | hældning af bane | rotationsperiode | densitet g/cm3 | Radio ækvator (km) | aksehældning | Nej. af satellitter |
|---|---|---|---|---|---|---|
| kviksølv | 7.0 | 58d.6 | 5.44 | 2 439 | <30 år | 0 |
| Venus | 3.4 | 243d | 5.24 | 6 051 | 177 ° | 0 |
| jorden | 0 | 23h.9 | 5.52 | 6 378 | 23rd.5 | 1 |
| Mars | 1st.8 | 24h.6 | 3.95 | 3 394 | 25 kr.2 | 2 |
| Jupiter | 1st.3 | 9h.9 | 1.33 | 71 398 | 3rd.1 | 16 |
| Saturn | 2nd.5 | 10 timer.2 | 0.69 | 60 000 | 26.4 | 17 |
| Uranus | 0 kr.8 | 10h.8 | 1.26 | 25 400 | 98 år | 5 |
| Neptun | 1st. 8 | 15h.8 | 1.67 | 24 750 | 29 kr | 2 |
satellitter
endelig giver vi nogle data om planeternes store satellitter. Jupiter og Saturn har mange satellitter, der er meget større end Mars, men vi nævner kun dem, der er ens i størrelse eller større end vores måne.
| Planet | satellitter | densitet g/cm3 | middelradius (km) | radiobane (103 km) | periode (dage) |
|---|---|---|---|---|---|
| jorden | Månen | 3.33 | 1 738 | 384.4 | 27.32 |
| Mars | Phobos | 2.1 | 13.5 | 9.38 | 0.319 |
| Deimos | 2.1 | 7.5 | 23.46 | 1.262 | |
| Jupiter | Io | 3.53 | 1 820 | 421.6 | 1.769 |
| Europa | 3.03 | 1 565 | 670.9 | 3.551 | |
| Ganymedes | 1.93 | 2 638 | 1 070 | 7.155 | |
| Calisto | 1.83 | 2 410 | 1 880 | 16.689 | |
| Saturn | Titan | 1.9 | 2 575 | 1 221.9 | 15.95 |
| Neptun | Nyt | 2 200 | 394.7 | 5.84 |
aktiviteter
- Bestem massen af planeten Jupiter fra radiodataene og revolutionsperioden for en af dens satellitter.
- Bestem radius af kredsløb om en satellit på planeten Jupiter fra massen af den planet og satellitens revolutionsperiode.
- Bestem intensiteten af gravitationsfeltet g på overfladen af planeterne og nogle satellitter ud fra dataene om deres masse M og deres radius R eller deres tæthed og deres radius.
eksempel: bestem massen af planeten Jupiter ved at vide, at radius af Io ‘ s kredsløb er 421.600 km, og at dens revolutionsperiode er 1.769 dage. Faktum: konstanten G er 6,67 * 10-11 Nm2 / kg2
eksempel: Beregn radiusen for satellitkallistens kredsløbat vide, at dens revolutionsperiode er 16.689 dage, og massen af planeten Jupiter er 1.901·1027 kg. Data: konstanten G er 6,67 * 10-11 Nm2 / kg2
g=G M R 2 = 4 liter 3 GPR
Data: konstanten G er 6.67 * 10-11 Nm2 / kg2
Månen
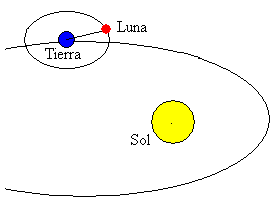
månen er en af de største kroppe i solsystemet. Dens bane er næsten cirkulær (ekscentricitet Kris=0,05), og planet for dens bane er tilbøjelig til 5 kilo i forhold til planet for Jordens bane.
den gennemsnitlige afstand mellem jordens centrum og månen er 384.400 km.Dens rotationsperiode omkring Jorden er 27.322 dage. Ændringen af månens position i forhold til solen giver anledning til Månens faser.
Månen præsenterer altid det samme ansigt for den jordbaserede observatør på grund af effekten af tidevandskræfterne, som Jorden udøver på Månen. Hvilket betyder, at månens rotationsperiode omkring sin akse falder sammen med den tid, det tager at fuldføre en bane rundt om Jorden.
månen er det himmelske objekt, der mest har fascineret den menneskelige art. Det tidligere Sovjetunionen sendte først et automatisk skib, der landede på Månens overflade i 1959. Den 20. juli 1969 var Neil Armstrong ledsaget af Aldrin de første mænd, der gik på Månens overflade som en del af Apollo 11-missionen. Det sidste besøg af amerikanske astronauter til Månen fandt sted i 1972.
månens oprindelse virker usikker, der er flere teorier:
-
det blev dannet på samme tid jorden med materialet fra en tåge
-
en himmellegeme er opdelt i to dele, der giver anledning til Jorden og Månen
-
at Månen dannede sig andetsteds og blev fanget af jorden
-
at jorden kolliderede med et himmelobjekt af stor størrelse (omtrent på størrelse med Mars eller større), og at Månen blev dannet med det materiale, der blev udvist fra denne kollision.
sidstnævnte teori synes i øjeblikket den mest accepterede af det videnskabelige samfund.
Månevej
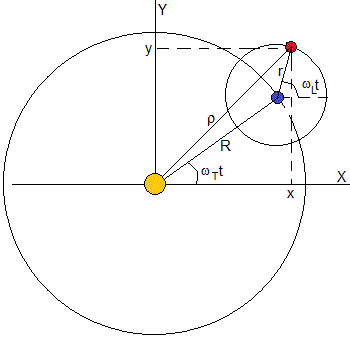
overvej en planet og dens satellit. Planeten beskriver en cirkulær bane med radius R omkring sin stjerne med konstant vinkelhastighed vægt=2 liter/PT, hvor PT er den periode eller tid, der fører til en komplet drejning. Satellit beskriver en cirkulær bane coplanaria med radius r med konstant vinkelhastighed wL=2π/PL, er PL den periode eller den tid, det tager at lave en fuldstændig revolution
position af satellitten i forhold til en reference system, hvis oprindelse er den stjerne, er
x=Rcos( ω T )+rcos( ω L-t ) y=Risiko( ω T )+risiko( ω L t )
Er α=wT/wL
{ x=Rcos( α-ω L t )+rcos( ω L-t ) y=Risiko( α-ω L t )+risiko( ω L t ) { x=Rcos( α 2π L P t )+rcos( 2π s P i L t ) y=Risiko( α 2π L P t )+risiko( 2π s P i L t )
vi vil Kalde τ=t/PL
x R =cos( α·2πτ )+ r-R cos( 2πτ ) og R =sin( α·2πτ )+ r-r sin( 2πτ )
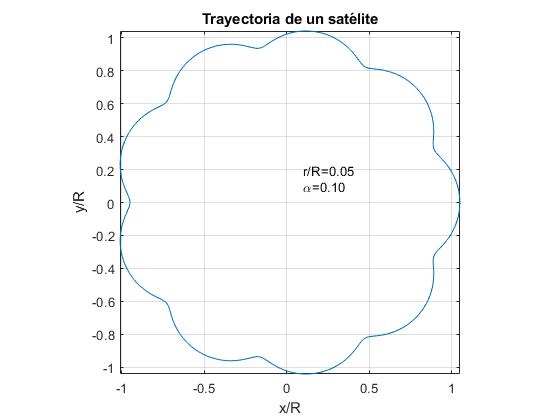
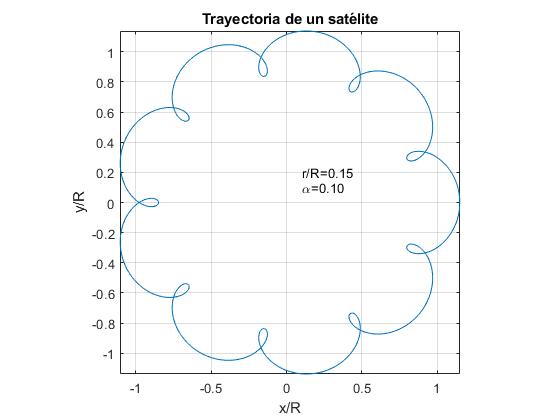
vi Repræsenterer bane af en satellit for α=0,1 og for tre værdier af forholdet r/R.
- r/R<α. Eksempel, r/R=0,05
- r / R=ren. Eksempel, r / R=0,1
- r/R >ren. Eksempel, r / R=0.15
alfa=0.1;r=0.15;fplot(@(t) r*cos(2*pi*t)+cos(2*pi*alfa*t), @(t) r*sin(2*pi*t)+sin(2*pi*alfa*t),)text(0.1,0.1,sprintf('\alpha=%1.2f',alfa))text(0.1,0.2,sprintf('r/R=%1.2f',r))axis equalgrid onxlabel('x/R')ylabel('y/R')title('Trayectoria de un satélite')
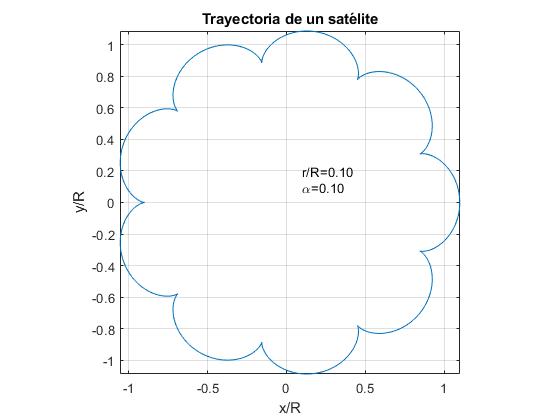
for Jorden og månen er dataene:
- radius af månens kredsløb: r=384,4 * 106 m, periode PL = 27,32 d
- radius af jordens kredsløb: R = 149, 6 * 109 m, periode PT = 365, 26 d
liter=vægt/vægt=PL/PT=0, 0748. r / R=0,0026
Månens bane vil ligne den første figur. I den grafiske repræsentation af bane om Månen for disse værdier af α og r/R ikke sætter pris på de svingninger af den radiale afstand mellem Solen og Månen
Acceleration af Månen
afstand ρ fra Solen til Månen, er
ρ 2 = x 2 + y 2 = R 2 + r 2 +2rRcos( ( ω L − ω T), t )
vi Beregne den rektangulære dele af acceleration
{ dx dt =− ω T Risiko( ω T )− ω L risiko( ω L t ) dy dt = ω T Rcos( ω T )+ ω L rcos( ω L t), {a x = d 2 x d-t 2 =− ω T 2 Rcos( ω T )− ω L 2 rcos( ω L-t ) y = d 2 y d t 2 =− ω T 2 Risiko( ω T )− ω L 2 risiko( ω L t )
den radiale del af Den acceleration
til ρ = a → · ρ → ρ = a x+ y, x 2 + y 2 =− ω T 2-R 2 + ω L 2 r 2 +( ω T 2 + ω L-2 )Rrcos( ( ω L − ω T), t ) R 2 + r 2 +2 rr cos( ( ω L − ω T), t )
minimum og maksimum værdier, der opnås, når cos((wL-wT)t)=±1
en max =− ω T 2-R 2 + ω L 2 r 2 +( ω T 2 + ω L-2 )Rr R 2 + r 2 +2 rr =−( ω T 2 R+ ω L 2 r ) min =− ω T 2-R 2 + ω L 2 r 2 −( ω T 2 + ω L-2 )Rr R 2 + r 2 -2 rr =−( ω T 2 R− ω L 2 r )
>> R=149.6e9; %Tierra>> r=384.4e3; %Luna>> wT=2*pi/(365*24*60*60) %velocidad angular TierrawT = 1.9924e-07>> wL=2*pi/(27.32*24*60*60) %velocidad angular TierrawL = 2.6619e-06>> aM=-(wT^2*R+wL^2*r)aM = -0.0059>> am=-(wT^2*R-wL^2*r)am = -0.0059
månen er den eneste satellit i solsystemet, hvis radiale komponent i accelerationen er negativ, det siges, at ‘Månen falder mod solen’,
månens faser
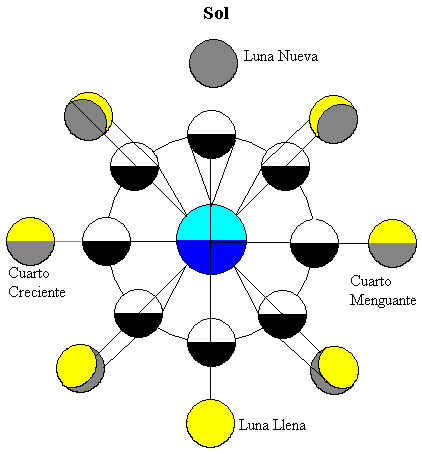
figuren viser månen i forskellige positioner i sin bane rundt om Jorden. Solen er langt væk og belyser begge himmellegemer (øverst på figuren)
halvdelen af Månen er oplyst af solen (i hvid farve), og halvdelen af Månen tættest på jorden er synlig af jordobservatør. Når Månen bevæger sig rundt om Jorden, ser vi forskellige fraktioner af den del, der er oplyst af Solen (de gule områder).
-
når månen er mellem Jorden og Solen, er den del af Månen, der er tættest på jorden, mørk, så vi kan ikke se månen, denne fase kaldes nymåne.
-
når jorden er mellem Solen og månen, er den del af Månen, der er tættest på Jorden, den oplyste halvdel, denne fase kaldes fuldmåne.
-
når månen er i mellempositioner, lyser kun halvdelen af den nærmeste del af jorden. Derfor ser vi kun en fjerdedel af Månen, disse to faser kaldes kvartaler, stigende eller faldende afhængigt af om den oplyste del, der er synlig fra Jorden, har tendens til at vokse eller falde.
Bemærk: Dette interaktive program forsøger at forklare månens faser, men det er en trofast repræsentation af Månens bane, som danner en vinkel på 5 liter med ekliptikens plan (Jordens bane omkring Solen) eller orienteringen af jordens akse, som er omkring 23 liter med det normale til ekliptikens plan.
en rød linje er trukket over månen, så læseren kan sætte pris på sammenfaldet mellem månens rotationsperiode omkring sin akse og den tid det tager at fuldføre en bane rundt om Jorden, og derfor har Månen altid det samme ansigt til jorden.
måneformørkelser
måneformørkelser forekommer, når månen er i fuld fase, og når Solen, Jorden og månen er i en lige linje. Så er Månen i skyggen produceret af jorden som vist på figuren.
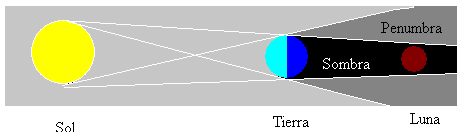
der er andre typer måneformørkelse, som afhænger af justeringen af de tre himmellegemer. Månen kan være i et ubelyst område (skygge) eller delvist oplyst (penumbra).
solformørkelsen opstår, når månen står mellem Solen og Jorden, Månen er i en ny fase. Månen er 400 gange mindre end Solen, men månen er 400 gange tættere på jorden, så den tilsyneladende størrelse af begge kroppe set fra jorden er næsten den samme. Månen kan således producere en total solformørkelse, hvis den observeres i skyggeområdet projiceret af Månen på jorden.
Månedata
| masse (kg) | 7.349·1022 |
| Radius (km) | 1737. 4 |
| gennemsnitlig massefylde (g/cm3) | 3.34 |
| gennemsnitlig afstand til jorden (km) | 384 000 |
| kredsløbsperiode (dage) | 27.32166 |
| Acceleration af tyngdekraften ved ækvator (m / s2) | 1.62 |
| ekscentricitet af bane | 0.0549 |
| hældning af bane (grader) | 5.1454 |
-
Beregn radius af månens cirkulære kredsløb omkring Jorden ved at vide, at perioden er 27,32 dage. Beregn også månens hastighed. Data: G =6,67 * 10-11 Nm2 / kg2, Jordens masse er M=5,98 * 1024 kg.
-
Beregn accelerationen af tyngdekraften g på Månens overflade.
-
Beregn kvotienten mellem solens diameter og Månens diameter. Beregn forholdet mellem den gennemsnitlige afstand mellem Solen og Jorden, og Månen og Jorden. Data: Solradius 6.96 * 108 m, Mellemjord – solafstand 1.49 * 1011 m
-
Beregn placeringen af jordens massecenter, målt fra Jordens centrum.
-
Beregn jordens tiltrækningskraft på Månen, sammenlign den med solens tiltrækningskraft på Månen. Datum: solmasse, 1,98 * 1030 kg
referencer
M. Marov. Planeter i solsystemet. Forlag Mir.
Lær mere om planeter i hvor mange planeter er der i vores solsystem?. ComofuncionaQue.com
til afsnittet ‘Månens bane’
David C. Johnston. Cycloidale stier i fysik som superpositioner af translationelle og roterende bevægelser. Er. J. Phys.87 (10), oktober 2019, s.808-810
månen vender altid mod solen. Math sider.