använda logaritmer i den verkliga världen

logaritmer finns överallt. Har du någonsin använt följande fraser?

• 6 siffror
• dubbelsiffror
• storleksordning
• ränta

du beskriver siffror i termer av deras befogenheter 10, en logaritm. Och en ränta är logaritmen för tillväxten i en investering.

förvånad över att logaritmer är så vanliga? Jag också. De flesta försök till matematik i den verkliga världen (TM) pekar på logaritmer i någon arcane formel, eller låtsas att vi är geologer fascinerade av Richter-skalan. ”Forskare bryr sig om loggar, och du borde också. Kan du också föreställa dig en värld utan zink?”

nej, nej, nej,nej nej, nej nej! (Mamma mia!)

Math uttrycker begrepp med notation som” ln ”eller”log”. Att hitta ”matematik i den verkliga världen” betyder att möta ideer i livet och se hur de kan skrivas med notation. Leta inte efter de bokstavliga symbolerna! När var sista gången du skrev en division tecken? När var sista gången du hackade upp lite mat?

Ok, ok, vi förstår det: vad handlar logaritmer om?

logaritmer hittar orsaken till en effekt, dvs ingången för viss utmatning

en vanlig ”effekt” ser något växa, som att gå från \$100 till \$150 om 5 år. Hur hände det här? Vi är inte säkra, men logaritmen finner en möjlig orsak: en kontinuerlig avkastning av ln(150/100) / 5 = 8,1% skulle stå för den förändringen. Det kanske inte är den faktiska orsaken (skedde all tillväxt under det sista året?), men det är ett smidigt genomsnitt vi kan jämföra med andra förändringar.

förresten, begreppet ”orsak och verkan” är nyanserad. Varför är 1000 större än 100?

• 100 är 10 som växte av sig själv för 2 tidsperioder ($10 * 10$)
• 1000 är 10 som växte av sig själv för 3 tidsperioder ($10 * 10 * 10$)

vi kan tänka på siffror som utgångar (1000 är ”1000 utgångar”) och ingångar (”hur många gånger behöver 10 växa för att göra dessa utgångar?”). Så,

1000 outputs > 100 outputs

eftersom

3 inputs > 2 inputs

eller med andra ord:

log(1000) > log(100)

Varför är detta användbart?

logaritmer sätter siffror på en mänsklig vänlig skala.

stora antal bryter våra hjärnor. Miljoner och biljoner är ”riktigt stora” trots att en miljon sekunder är 12 dagar och en biljon sekunder är 30 000 år. Det är skillnaden mellan ett amerikanskt semesterår och hela den mänskliga civilisationen.

tricket att övervinna ” stort antal blindhet ”är att skriva siffror i termer av” ingångar ” (dvs. deras kraftbas 10). Denna mindre skala (0 till 100) är mycket lättare att förstå:

• effekt av 0 = $10^0$ = 1 (enstaka objekt)
• effekt av 1 = $10^1$ = 10
• effekt på 3 = $10^3$ = tusen
• effekt på 6 = $10^6$ = miljoner
• effekt på 9 = $10^9$ = miljarder
• effekt på 12 = $10^12$ = biljoner
• effekt på 23 = $10^23$ = antal molekyler i ett dussin gram kol
• effekt på 80 = $10^80$ = antal molekyler i universum

en skala från 0 till 80 tog oss från ett enda objekt till antalet saker i universum. Inte för illa.

logaritmer räknar multiplikation som steg

logaritmer beskriver förändringar i termer av multiplikation: i exemplen ovan är varje steg 10x större. Med den naturliga loggen är varje steg ”e” (2.71828…) gånger mer.

när man hanterar en serie multiplikationer hjälper logaritmer att” räkna ” dem, precis som tillägg räknas för oss när effekter läggs till.

Visa mig matematiken

tid för köttet: låt oss se var logaritmer dyker upp!

sexsiffrig lön eller 2-siffrig kostnad

vi beskriver siffror i termer av deras siffror, dvs. hur många befogenheter 10 de har (är de i tiotals, hundratals, tusentals, tiotusen, etc.). Att lägga till en siffra betyder ”multiplicera med 10”, dvs.

logaritmer räknar antalet multiplikationer som läggs till, så från och med 1 (en enda siffra) lägger vi till ytterligare 5 siffror ($10^5$) och 100 000 får ett 6-siffrigt resultat. Att prata om ”6” istället för ”hundra tusen” är kärnan i logaritmer. Det ger en grov känsla av skala utan att hoppa in i detaljer.

Bonusfråga: hur skulle du beskriva 500 000? Att säga ”6-figur” är vilseledande eftersom 6-figurer ofta innebär något närmare 100 000. Skulle” 6.5 figur ” fungera?

inte riktigt. I våra huvuden betyder 6,5 ”halvvägs” mellan 6 och 7 figurer, men det är en adderares tankegång. Med logaritmer a”.5 ” betyder halvvägs när det gäller multiplikation, dvs kvadratroten ($9^.5$ betyder kvadratroten av 9 — 3 är halvvägs när det gäller multiplikation eftersom det är 1 till 3 och 3 till 9).

med log (500 000) får vi 5,7, Lägg till 1 för den extra siffran, och vi kan säga ”500 000 är en 6.7 Figur nummer”. Prova det här:

storleksordning

vi nördar älskar denna fras. Det betyder ungefär” 10x skillnad ”men låter bara svalare än”1 siffra större”.

i datorer, där allt räknas med bitar (1 eller 0), har varje bit en fördubblingseffekt (inte 10x). Så att gå från 8 till 16 bitar är ”8 storleksordningar” eller $2^8 = 256$ gånger större. (”Större” hänvisar i detta fall till mängden minne som kan adresseras.) Att gå från 16 till 32 bitar betyder en extra 16 storleksordningar, eller $2^16$ ~ 65,536 gånger mer minne som kan adresseras.

räntor

Hur räknar vi ut tillväxttakten? Ett land har inte för avsikt att växa med 8,56% per år. Du tittar på BNP ett år och BNP nästa och tar logaritmen för att hitta den implicita tillväxttakten.

mina två favorit tolkningar av den naturliga logaritmen (ln (x)), dvs den naturliga loggen av 1.5:

• om du antar 100% tillväxt, hur länge behöver du växa för att komma till 1.5? (.405, mindre än hälften av tidsperioden)
• förutsatt 1 tidsenhet, hur snabbt behöver du växa för att komma till 1,5? (40.5% per år, kontinuerligt sammansatt)

logaritmer är hur vi räknar ut hur snabbt vi växer.

mätskala: Google PageRank

Google ger varje sida på webben en poäng (PageRank) som är ett grovt mått på auktoritet / betydelse. Detta är en logaritmisk skala, som i mitt huvud betyder ”PageRank räknar antalet siffror i din poäng”.

så, en webbplats med pagerank 2 (”2 siffror”) är 10x mer populär än en PageRank 1-webbplats. Min webbplats är PageRank 5 och CNN har PageRank 9, så det finns en skillnad på 4 storleksordningar ($10^4$ = 10,000).

grovt sett får jag cirka 7000 besök / dag. Med hjälp av min kuvertmatematik kan jag gissa att CNN får cirka 7000 * 10 000 = 70 miljoner besök / dag. (Hur gjorde jag det? I mitt huvud tror jag $7k * 10k = 70 * k * k = 70 * m$). De kan ha några gånger mer än det (100m, 200m) men förmodligen inte upp till 700M.

Google förmedlar mycket information med en mycket grov skala (1-10).

mätskala: Richter, Decibel, etc.

suck. Vi är på den typiska” logaritmer i den verkliga världen ” exempel: Richter skala och Decibel. Tanken är att sätta händelser som kan variera drastiskt (jordbävningar) på en enda skala med ett litet intervall (vanligtvis 1 till 10). Precis som PageRank är varje 1-punktsökning en 10x förbättring av kraften. Den största jordbävningen som registrerades av människor var 9,5; Yucat usci-halvön, som sannolikt gjorde dinosaurierna utrotade, var 13.

decibel är liknande, även om det kan vara negativt. Ljud kan gå från intensivt tyst (pindrop) till extremt högt (flygplan) och våra hjärnor kan bearbeta allt. I verkligheten är ljudet av ett flygplans motor miljoner (miljarder, trillioner) gånger kraftigare än en pindrop, och det är obekvämt att ha en skala som går från 1 till en gazillion. Loggar håller allt i rimlig skala.

logaritmiska grafer

du ser ofta objekt ritade på en ”loggskala”. I mitt huvud betyder det att en sida räknar ”antal siffror” eller ”antal multiplikationer”, inte själva värdet. Återigen hjälper detta att visa vildt varierande händelser i en enda skala (går från 1 till 10, inte 1 till miljarder).

Moores lag är ett bra exempel: vi fördubblar antalet transistorer var 18: e månad (bild med tillstånd Wikipedia).

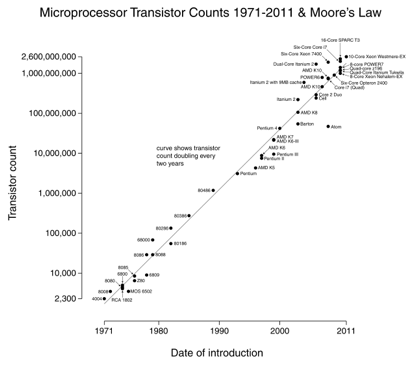
det snygga med log-scale-grafer är exponentiella förändringar (processorhastighet) visas som en rak linje. Att växa 10x per år betyder att du stadigt marscherar upp ”siffror” – skalan.

framåt och uppåt

om ett koncept är välkänt men inte älskat betyder det att vi måste bygga vår intuition. Hitta analogier som fungerar, och inte nöja sig med slop en lärobok kommer trav ut. I mitt huvud:

• logaritmer hittar grundorsaken till en effekt (se tillväxt, hitta ränta)
• de hjälper till att räkna multiplikationer eller siffror, med bonusen för partiella räkningar (500k är ett 6,7 siffrigt nummer)

Glad matte.

andra inlägg i denna serie

1. en intuitiv Guide till exponentiella funktioner & e
2. avmystifiera den naturliga logaritmen (ln)
3. en visuell Guide till enkla, sammansatta och kontinuerliga räntor
4. vanliga definitioner av e (Colorized)
5. förstå exponenter (varför gör 0^0 = 1?)
6. använda logaritmer i den verkliga världen
7. hur man tänker med exponenter och logaritmer
8. förstå diskret vs kontinuerlig tillväxt
9. Vad betyder en exponent egentligen?
10. f: Varför är e speciell? (2.718…, inte 2, 3.7 eller ett annat nummer?)