Bootstrap i r
Bootstrap är en metod för slutsats om en population med hjälp av provdata.Bradley Efron introducerade det först i dettapapper 1979.Bootstrap förlitar sig på provtagning med ersättning från provdata. Thistechnique kan användas för att uppskatta standardfelet för någon statistik och toobtain ett konfidensintervall (CI) för det. Bootstrap är särskilt användbarnär CI inte har en sluten form, eller den har en mycket komplicerad.
Antag att vi har ett urval av n-element: X = {x1, x2, …, xn} och viär intresserade av CI för viss statistik T = T(X). Bootstrapframework är enkelt. Vi upprepar bara R gånger följande schema: för i-th repetition, prov med ersättnings n element från det tillgängliga provet (vissa av dem kommer att plockas mer än en gång). Ring thisnew prov i-th bootstrap prov, Xi, och calculatedesired statistik Ti = t (Xi).
som ett resultat får vi R-värden för vår statistik: T1, T2,…, TR. Vi kallar thembootstrap realiseringar av T eller en bootstrap distribution av T. baserat på det, vi kan beräkna CI för T. Det finns flera sätt ofdoing detta. Att ta percentiler verkar vara det enklaste.
Bootstrap i aktion
Låt oss använda (återigen) välkända iris dataset. Ta en titt på en firstfew rader:
Antag att vi vill hitta CIs för median Sepal.Length, medianSepal.Width och Spearmans rank korrelationskoefficient mellan dessatvå. Vi använder R’s boot paket och en funktion som kallas… boot. För att använda sin kraft måste vi skapa en funktion som beräknar ourstatistic(s) av omsamplade data. Det bör ha minst tvåargument: en dataset och en vektor som innehåller indices av elementfrån en dataset som plockades för att skapa ett bootstrap-prov.
om vi vill beräkna CIs för mer än en statistik på en gång måste ourfunction returnera dem som en enda vektor.
för vårt exempel kan det se ut så här:
library(boot)foo <- function(data, indices){ dt<-data c( cor(dt, dt, method='s'), median(dt), median(dt) )}foo väljer önskade element (vilka siffror lagras i indices) från data och beräknar korrelationskoefficienten för de två första kolumnerna(method='s' används för att välja Spearmans rangkoefficient,method='p' kommer att resultera med Pearsons koefficient) och deras medianer.
vi kan också lägga till några extra argument, t.ex. låt användaren välja typ odcorrelation koefficient:
foo <- function(data, indices, cor.type){ dt<-data c( cor(dt, dt, method=cor.type), median(dt), median(dt) )}för att göra denna handledning mer generell använder jag den senare versionen avfoo.
nu kan vi använda funktionen boot. Vi måste leverera det med ett namn oddataset, funktion som vi just har skapat, antal repetitioner (R)och eventuella ytterligare argument för vår funktion (som cor.type). Nedan använder jag set.seed för reproducerbarhet av detta exempel.
set.seed(12345)myBootstrap <- boot(iris, foo, R=1000, cor.type='s')boot funktionen returnerar ett objekt av den klass som kallas… (ja, du har rätt!)boot. Den har två intressanta element. $t innehåller R-värden för ourstatistic (s) som genereras av bootstrap-proceduren (bootstrap-realiseringar ofta):
$t0 innehåller värden för vår statistik (er) i original, full, dataset:
myBootstrap$t0## -0.1667777 5.8000000 3.0000000utskrift boot objekt till konsolen ger ytterligare information:
original är samma som $t0. bias är en skillnad mellan medelvärdet av Bootstrap-realiseringar (de från $t), kallad en bootstrap estimateof T och värde i originaldataset (den från $t0).
colMeans(myBootstrap$t)-myBootstrap$t0## 0.002546391 -0.013350000 0.007900000std. error är ett standardfel för bootstrap-uppskattning, vilket är lika medstandardavvikelse för bootstrap-realiseringar.
apply(myBootstrap$t,2,sd)## 0.07573983 0.10295571 0.02726414olika typer av bootstrap CIs
innan vi börjar med CI är det alltid värt att ta en titt pådistribution av bootstrap-realiseringar. Vi kan använda funktionen plot, medindex som berättar vilken statistik som beräknas i foo vi vill se. Här är index=1 en Spearmans korrelationskoefficient mellansepal längd och bredd,index=2är en median od sepal längd och index=3 är en median od sepal bredd.
plot(myBootstrap, index=1)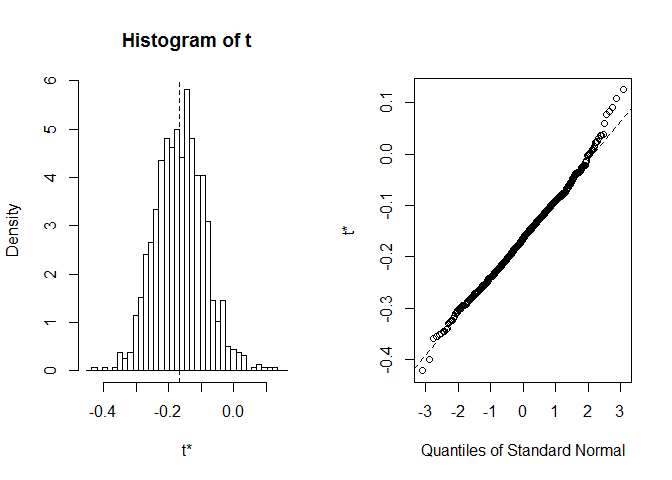
fördelningen av bootstrap korrelationskoefficienter verkar ganskanormal. Låt oss hitta CI för det. Vi kan använda boot.ci. Det är standard till95 procent CIs, men det kan ändras med parametern conf.
boot.ci ger 5 typer av bootstrap CIs. En av dem, studentizedinterval, är unik. Det behöver en uppskattning av bootstrap varians. Vi tillhandahåller inte det, så R skriver ut en varning:bootstrap variances needed for studentized intervals. Varianceestimates kan erhållas med andra nivå bootstrap eller (lättare) withjackknife teknik. Detta ligger på något sätt utanför ramen för denna handledning,så låt oss fokusera på de återstående fyra typerna av bootstrap CIs.
om vi inte vill se dem alla kan vi välja relevanta i argumentet type. Möjliga värden är norm, basic, stud, perc, bca ora vektor av dessa.
funktionen boot.ci skapar objekt för klassen… (ja, du har gissat!)bootci. Dess element kallas precis som typer av CI som används i type argument. $norm är en 3-elementsvektor som innehåller konfidensnivåoch CI-gränser.
boot.ci(myBootstrap, index=1, type='norm')$norm## conf ## 0.95 -0.3177714 -0.02087672$basic, $stud, $perc och $bca är 5-elementsvektorer som innehålleräven percentiler som används för att beräkna CI (vi kommer tillbaka till det senare):
boot.ci(myBootstrap, index=1, type='basic')$basic## conf ## 0.95 975.98 25.03 -0.3211981 -0.03285178lite notation (förlåt!)
för att få en känsla av vilka olika typer av CI är, måste vi introduceranågon notation. Så låt:
- t⋆ vara bootstrap-skattningen (medelvärdet av bootstraprealizations),
- t0 ett värde av vår statistik i den ursprungliga datasetet
- se⋆ vara ett vanligt fel av bootstrap-skattningen,
- b vara en inriktning av bootstrap estimateb = t⋆ − t0
- α vara en konfidensnivå, typiskt α = 0.95,
- za vara en $1-\frac \alfa-2 – $-kvantilen av standardnormal distribution
- θα vara en α-percentilen av fördelningen av bootstraprealizations.
percentil CI
med ovanstående notation är percentil CI:
så detta tar bara relevanta percentiler. Inget mer.
Normal CI
en typisk Wald CI skulle vara:
men i bootstrap-fallet borde vi korrigera det för partiskhet. Så blir det:
$ $ t_0-b \ pm z_ \ alpha \ cdot se^ \ star \ \ 2t_0-t^\star \pm z_\alpha \cdot se^\star$$
grundläggande CI
percentil CI rekommenderas vanligtvis inte eftersom det fungerar dåligtnär det gäller konstiga-tailed distributioner. Grundläggande CI (även kalladpivotal eller empirisk CI) är mycket mer robust för detta. De rationalebehind det är att beräkna skillnader mellan varje bootstrap replicationand t0 och använda percentiler av deras distribution. Fulldetails kan hittas, t. ex. i L. Wassermans All ofStatistics
Slutformel för grundläggande CI är:
BCa CI
BCa kommer från bias-korrigerad, accelererad. Formelnför det är inte särskilt komplicerat men något ointuitivt, så jag hoppar över det.Se artikel av Thomas J. DiCiccio och BradleyEfron om du är intresserad av detaljer.
Acceleration som nämns i metodens namn kräver användning av specifikapercentiler av bootstrap-realiseringar. Ibland kan det hända attdessa skulle vara några extrema percentiler, eventuellt avvikare.BCa kan vara instabil i sådana fall.
Låt oss titta på BCa CI för kronblad bredd median. Inoriginal dataset, denna median motsvarar exakt 3.
vi får BCa CI (2.9, 2.9). Det är konstigt, men lyckligtvis Rvarnade oss för att extreme order statistics used as endpoints. Låt oss sevad exakt hände här:
plot(myBootstrap, index=3)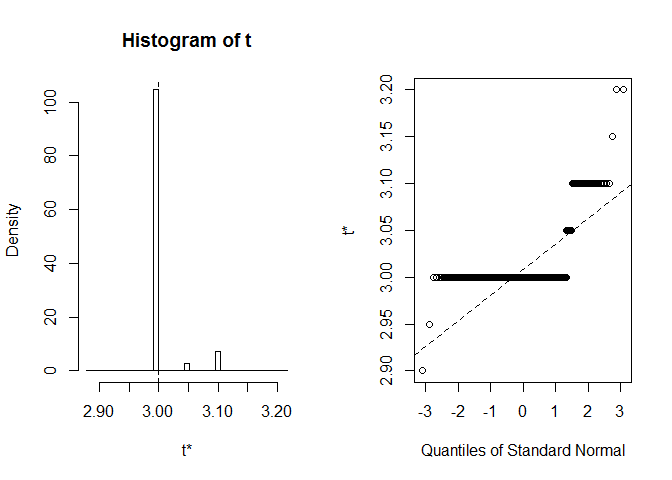
Distribution av bootstrap-realiseringar är ovanligt. En stor majoritet av dem (över 90%) är 3s.
table(myBootstrap$t)#### 2.9 2.95 3 3.05 3.1 3.15 3.2## 1 1 908 24 63 1 2replikering av resultat
ibland måste vi återskapa bootstrap-replikationer. Om vi kan använda Rför det är detta inte ett problem. set.seed funktionen löser problemet.Att återskapa bootstrap-replikationer i annan programvara skulle vara mycket merkomplex. Vad är mer, för stora R, omräkning i R kan ocksåinte vara ett alternativ (på grund av brist på tid, till exempel).
vi kan hantera detta problem, spara index för element i originaldataset, som bildade varje bootstrap-prov. Detta är vad boot.arrayfunktion (med indices=T argument) gör.
tableOfIndices<-boot.array(myBootstrap, indices=T)varje rad är ett bootstrap-prov. T. ex., innehåller vårt första provföljande element:
inställning indices=F (en standard) får vi svar på frågan ”hur många gånger varje element i originaldataset uppträdde i varje bootstrapsample?”. Till exempel i det första provet: det 1: a elementet i datauppsättningen dök uppen gång, 2: a elementet visade sig inte alls, 3: e elementet dök upp en gång, 4: etvå gånger och så vidare.
en tabell som denna tillåter oss att återskapa bootstrap realisering utanför R.Eller i R själv när vi inte vill använda set.seed och göra all thecomputation igen.
onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')Låt oss kontrollera om resultaten är desamma:
ja, de är!
om du vill lära dig mer om maskininlärning i R, ta Datacamps Machine Learning Toolbox-kurs.