Dold Markov-modell: enkel Definition och översikt

Statistikdefinitioner >

den dolda Markov-modellen (HMM) är ett relativt enkelt sätt att modellera sekventiella data. En dold Markov-modell innebär att Markov-modellen som ligger till grund för data är dold eller okänd för dig. Mer specifikt vet du bara observationsdata och inte information om Staterna. Med andra ord finns det en specifik typ av modell som producerar data (en Markov-modell) men du vet inte vilka processer som producerar den. Du använder i princip din kunskap om Markov-modeller för att göra en utbildad gissning om modellens struktur.

Vad är en Markov-Modell?

för att avslöja den dolda Markov-modellen måste du först förstå vad en Markov-modell är i första hand. Här skapar jag ett enkelt exempel med två saker som är mycket bekanta med Sannolikhet: tärningar och påsar med färgade bollar.

modellkomponenterna, som du använder för att skapa den slumpmässiga modellen, är:

• en sexsidig röd dö.
• en tio-sidig svart dö.
• en röd väska med tio bollar. Nio bollar är röda, en är svart.
• en svart väska med tjugo bollar. En boll är röd, nitton är svart.

”svart” och ”rött” är de två tillstånden i denna modell (med andra ord kan du vara svart eller du kan vara röd).
skapa nu modellen genom att följa dessa steg:

1. UTSLÄPPSSTEG: rulla en matris. Notera numret som kommer upp. Detta är utsläppet. I ovanstående grafik valde jag en röd dö för att starta (godtycklig — jag kunde ha valt svart) och rullade 2.
2. övergångssteg: Välj slumpmässigt en boll från påsen med färgen som matchar formen du rullade i steg 1. Jag rullade en röd dö, så jag ska välja en boll från den röda väskan. Jag drog ut en svart boll, så jag ska övergå till black die för nästa utsläpp.

du kan sedan upprepa dessa steg till ett visst antal utsläpp. Om du till exempel upprepar denna sekvens av steg 10 gånger kan du ge dig uppsättningen {2,3,6,1,1,4,5,3,4,1}. Processen att övergå från ett tillstånd till ett annat kallas en Markov-process.

övergången från rött till svart eller svart till rött har olika sannolikheter eftersom det finns olika antal svarta och röda bollar i påsarna. Följande diagram visar sannolikheten för den här modellen, som har två tillstånd (svart och rött):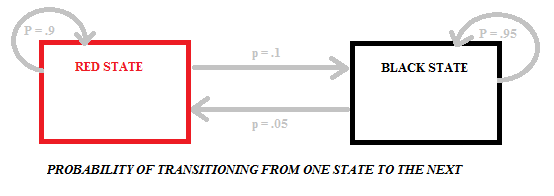

Dold Markov – Modellnotation

https: / / = (A,B,), är en förkortning för en HMM. Annan notation används i dolda Markov-modeller:

• A = tillståndsövergångssannolikheter (aij)
• B = observationssannolikhetsmatris (bj(k))
• N = antal tillstånd i modellen {1,2…N} eller tillståndet vid tiden t-oc t
• m = antal distinkta observationssymboler per tillstånd
• Q = {q0, Q1, . . . , qN−1} = distinkta tillstånd i Markov-processen
• T = längden på observationssekvensen
• V = {0, 1, . . . , M − 1} = uppsättning möjliga observationer
• O = (O0, O1,. . . , OT -1) = observationssekvens
• POV = initial tillståndsfördelning (ni)
• s = tillstånd eller tillståndssekvens (s1, s2… sn)
• xk = dold tillstånd
• zk = observation.

tre grundläggande problem

tre grundläggande problem kan lösas med dolda Markov modeller:

1. med tanke på den dolda Markov-modellen 2x = (A, B, 2x) och en sekvens av observationer O, hitta sannolikheten för en observation p(o | 2x). Detta kallas ibland Utvärderingsproblemet.
2. med tanke på den dolda Markov-modellen Asia = (A, B, Asia) och en observationssekvens O, hitta den mest sannolika tillståndssekvensen (s1, s2… sn). Detta kallas ibland ett Avkodningsproblem.
3. hitta en observationssekvens (O1, O2…på och dold Markov-Modell 0 = (A, B, 2) som maximerar sannolikheten för O. Detta kallas ibland ett inlärningsproblem eller optimeringsproblem.

Rabiner, L. R.” en handledning om dolda Markov-modeller och utvalda applikationer i taligenkänning”, Proceedings of the IEEE, vol.77, s. 257-286, Feb. 1989.
Stämpel, M. (2013). En avslöjande introduktion till dolda Markov-modeller. Hämtad 8/6/2013 från: http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf

——————————————————————————

behöver du hjälp med en läxa eller testfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert på området. Dina första 30 minuter med en Chegg-handledare är gratis!