En cirkel är jämnt uppdelad i sex lika trianglar
Hej Marilynn,
först kommer jag att berätta mina antaganden om hur din bild ser ut:
- varje triangel har ett toppunkt (hörn) i mitten av cirkeln
- varje triangel har hörn på cirkelns omkrets (så två sidor av varje triangel är en radie)
- trianglarna delar sidor (det finns inga gapar mellan trianglarna)
den övergripande bilden ser ut som en blomma – varje triangel är en kronblad.

det okända området är det som finns kvar runt utsidan av cirkeln, mellan omkretsen och utsidan av varje triangel. Detta okända område är uppdelat i sex kongruenta sektioner (lika på alla sätt – som trianglarna är ”lika” på alla sätt – inklusive område, sidans längd och bågens längd). Det är inte klart om du menar att området för en båge är Pi (inte faktiskt delad paj, även om det är samma), eller alla sex sektionerna tillsammans är Pi. I det följande antar jag att en av de yttre sektionerna har ett område med Pi, så att området för alla sex sektionerna tillsammans är 6 gånger Pi. Vi måste hitta cirkelns radie, kalla den r.
jag kommer också att använda P för att stå för Pi (eller ca. 3.14). Nu finns det mycket information vi kan garnera från trianglarna:
- vinklarna i mitten är alla 60 grader. Detta beror på att de sex vinklarna i mitten är alla lika och en cirkel har 360 grader. Så gör 360 edivided med 6.
- varje triangel är likbent. Detta beror på att två sidor är lika (sidorna som är en radie).
- varje triangel är faktiskt liksidig. Eftersom det är iscoceles är de två yttre vinklarna också lika. Men det finns 180 grader i en triangel, 60 används redan i mittvinkeln och lämnar 180-60=120 grader för yttervinklarna. Men 120 dividerat med 2 är 60 grader, så alla tre vinklarna är lika, så det är isoscles.
- varje sida i varje triangel är av längd r. Detta beror på att vi har 6 kongruenta (”lika” på alla sätt) liksidiga trianglar, och eftersom två sidor av varje triangel är en radie.
från trianglarnas geometri behöver vi göra lite algebra. Eftersom vi känner till ett område, och vi behöver en radie, behöver vi en formel (eller ekvation) för radie i termer av område (i det som följer, håll målet med en formel i åtanke). Cirkelns område är P * r2 (r2 betyder R kvadrat och * betyder multiplicera) området för de kvarvarande sektionerna utanför trianglarna, men inuti cirkeln (ett område som vi redan inte ska vara 6*P), kan också hittas genom att subtrahera trianglarnas område från cirkelns område. Vi måste hitta ett område av en av de liksidiga trianglarna.
Metod 1 för att beräkna ett område i en triangel
området för en triangel är b*h/2 Det är här som en del trigonometri behövs: rita en linje från ett toppunkt till en motsatt sida som delar motsatt sida i hälften och ligger i rät vinkel. Detta delar den liksidiga triangeln i två kongruenta rätvinkliga trianglar, och den nya sidan är höjden, kalla den h. Vi måste hitta h.
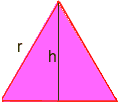
med trig i en av de rätvinkliga trianglarna har vi sin60 = h / r men sin60 = sqr (3) / 2, där sqr(3) betyder kvadratroten av tre så sqr(3)/2 = h/r multiplicera båda sidor med r för att få h = r*sqr (3)/2 r nu är området för en liksidig triangel b*h/2 = (r)*(r * sqr(3)/2)/2 = (r2)*sqr(3)/4 r = sqr(6*P/(P-6 * sqr(3)/4)) Använd order av operationer för att beräkna på en räknare (med P=3.14): r= 5.896… Så är cirkelns radie ca. 5.9. Paul