skillnad mellan IIR-och FIR-filter: en praktisk designguide

BY admin

| oktober 26, 2021

ett digitalt filter är en matematisk algoritm som fungerar på en digital dataset (t.ex. sensordata) för att extrahera information av intresse och ta bort oönskad information. Tillämpningar av denna typ av teknik inkluderar att ta bort glitches från sensordata eller till och med städa upp brus på en uppmätt signal för enklare dataanalys. Men hur väljer vi den bästa typen av digitalt filter för vår applikation? Och vad är skillnaderna mellan ett IIR-filter och ett FIR-filter?

digitala filter är indelade i följande två kategorier:

oändligt impulsrespons (IIR)
ändligt impulsrespons (FIR)

som namnen antyder kategoriseras varje typ av filter efter längden på dess impulsrespons. Innan man börjar med en detaljerad matematisk analys är det dock klokt att uppskatta skillnaderna i prestanda och egenskaper hos varje typ av filter.

exempel

för att illustrera skillnaderna mellan en IIR och FIR visas frekvensresponsen för en 14: e ordning FIR (heldragen linje) och en 4: e ordning Chebyshev typ I IIR (streckad linje) nedan i Figur 1. Observera att även om storleksspektra har en liknande grad av dämpning, är IIR-filterets fasspektrum icke-linjärt i passbandet (\(\small 0\rightarrow7.5HZ\)) och blir mycket icke-linjärt vid avstängningsfrekvensen, \(\small f_c=7.5 Hz\). Observera också att FIR kräver ett högre antal koefficienter (15 vs IIR: s 10) för att matcha IIR: s dämpningsegenskaper.

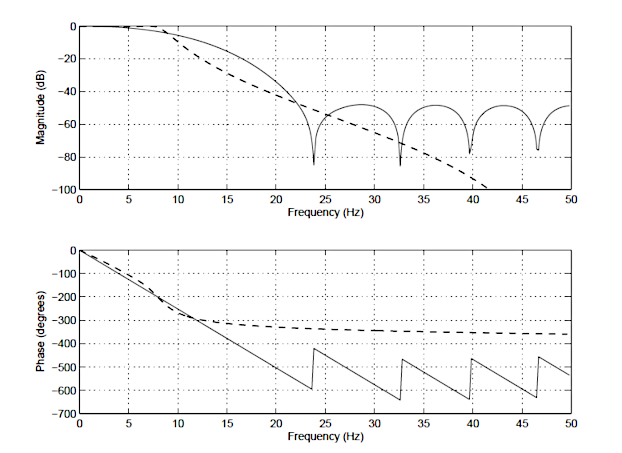
dessa är bara några av skillnaderna mellan de två typerna av filter. En detaljerad sammanfattning av de viktigaste fördelarna och nackdelarna med varje typ av filter kommer nu att följa.

IIR-filter

IIR-filter (infinite impulse response) väljs vanligtvis för applikationer där linjär fas inte är för viktig och minnet är begränsat. De har använts i stor utsträckning inom ljudutjämning, biomedicinsk sensorsignalbehandling, IoT/IIoT smarta sensorer och höghastighets telekommunikation/RF-applikationer.

fördelar

låg implementeringskostnad: kräver mindre koefficienter och minne än FIR-filter för att uppfylla en liknande uppsättning specifikationer, dvs cut-off frekvens och stoppband dämpning.
låg latens: lämplig för realtidskontroll och mycket höghastighets RF-applikationer på grund av det låga antalet koefficienter.
Analog ekvivalent: kan användas för att efterlikna egenskaperna hos analoga filter Med hjälp av S-z-planmappningstransformationer.

nackdelar

icke-linjära fasegenskaper: Faskaraktäristiken hos ett IIR-filter är i allmänhet olinjär, särskilt nära avstängningsfrekvenserna. All-pass Utjämningsfilter kan användas för att förbättra passbandsfasegenskaperna.
mer detaljerad analys: kräver mer skalning och numerisk överflödesanalys när den implementeras i fast punkt. Den direkta form II – filterstrukturen är särskilt känslig för kvantifieringens effekter och kräver särskild omsorg under designfasen.
numerisk stabilitet: Mindre numeriskt stabil än deras fir (finita impulsrespons) motsvarigheter, på grund av återkopplingsvägarna.

FIR-filter

FIR-filter (finite impulse response) väljs vanligtvis för applikationer där linjär fas är viktig och en anständig mängd minne och beräkningsprestanda finns tillgängliga. De har en brett utplacerad i ljud-och biomedicinska signalförbättringsapplikationer. Deras All-zero-struktur (diskuteras nedan) säkerställer att de aldrig blir instabila för någon typ av ingångssignal, vilket ger dem en tydlig fördel jämfört med IIR.

fördelar

linjär fas: granar kan enkelt utformas för att ha linjär fas. Detta innebär att ingen fasförvrängning införs i signalen som ska filtreras, eftersom alla frekvenser skiftas i tid med samma mängd – vilket bibehåller deras relativa harmoniska relationer (dvs. konstant grupp-och fasfördröjning). Detta är verkligen inte fallet med IIR-filter, som har en icke-linjär faskaraktäristik.
stabilitet: eftersom granar inte använder tidigare utgångsvärden för att beräkna sin nuvarande utgång, dvs. de har ingen feedback, de kan aldrig bli instabila för någon typ av ingångssignal, vilket ger dem en tydlig fördel jämfört med IIR-filter.
godtyckligt frekvenssvar: Parks-McClellan och ASN Filterscripts firarb () – funktion möjliggör utformning av en FIR med ett godtyckligt magnitudsvar. Detta innebär att en FIR kan anpassas lättare än en IIR.
fastpunktsprestanda: effekterna av kvantifiering är mindre allvarliga än för en IIR.

nackdelar

högt beräknings-och minneskrav: FIRs kräver vanligtvis många fler koefficienter för att uppnå en skarp avstängning än deras IIR-motsvarigheter. Konsekvensen av detta är att de kräver mycket mer minne och betydligt en högre mängd MAC (flera och ackumulera) operationer. Men moderna mikrokontrollerarkitekturer baserade på Arms Cortex-M-kärnor inkluderar nu DSP-hårdvarustöd via SIMD (signalinstruktion, flera data) som påskyndar filtreringsoperationen avsevärt.
högre latens: det högre antalet koefficienter innebär att en FIR i allmänhet är mindre lämplig än en IIR för snabba applikationer med hög genomströmning. Detta blir problematiskt för applikationer med sluten slinga i realtid, där ett FIR-filter kan ha för mycket gruppfördröjning för att uppnå slingstabilitet.
ingen analog ekvivalent: med hjälp av den Bilinära, matchade z-transformen (s-z mapping) kan ett analogt filter enkelt omvandlas till ett ekvivalent IIR-filter. Detta är dock inte möjligt för en FIR eftersom den inte har någon analog ekvivalent.

matematiska definitioner

som diskuterats i inledningen kommer namnet IIR och FIR från de matematiska definitionerna av varje typ av filter, dvs ett IIR-filter kategoriseras av dess teoretiskt oändliga impulsrespons,

\(\displaystyle
y (n)= \ sum_{k = 0}^{\infty}h (k)x (n-k)
\)

och en FIR kategoriserad av dess ändliga impulsrespons,

\(\displaystyle
y (n)= \ sum_{k = 0}^{N-1}h (k)x (n-k)
\)

vi kommer nu att analysera de matematiska egenskaperna för varje typ av filter i tur och ordning.

IIR definition

som sett ovan kategoriseras ett IIR-filter Med dess teoretiskt oändliga impulsrespons,

\(\displaystyle y (n)=\sum_{k = 0}^{\infty}h(k) x(n-k)\)

praktiskt taget är det inte möjligt att beräkna utgången från en IIR med denna ekvation. Därför kan ekvationen skrivas om i termer av ett ändligt antal poler \(\small p\) och nollor \(\small q\), som definieras av den linjära konstanta koefficientskillnadsekvationen som ges av:

\(\displaystyle
y (n)= \ sum_{k = 0}^{q}b_k x (n-k)- \ sum_{k=1}^{p}a_ky(n-k)
\)

där, \(\small a_k\) och \(\small b_k\) är filtrets nämnare och täljarpolynomkoefficienter, vars rötter är lika med filtrets poler respektive nollor. Således kan ett förhållande mellan skillnadsekvationen och z-transform (överföringsfunktionen) därför definieras med hjälp av z-transform delay-egenskapen så att,

\(\displaystyle
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{- K}}{1+ \ sum\limits_{k = 1}^p a_kz^{- k}}
\)

som sett är överföringsfunktionen en frekvensdomänrepresentation av filtret. Observera också att polerna verkar på utgångsdata och nollorna på ingångsdata. Eftersom polerna verkar på utgångsdata och påverkar stabiliteten är det viktigt att deras radier förblir inuti enhetscirkeln (dvs. <1) för BIBO (bounded input, bounded output) stabilitet. Nollornas radier är mindre kritiska, eftersom de inte påverkar filterstabiliteten. Detta är den främsta anledningen till att all-zero FIR (finite impulse response) filter alltid är stabila.

Bibo stabilitet

ett linjärt tidsinvariant (Lti) system (t.ex. ett digitalt filter) sägs vara avgränsad ingång, avgränsad utgång stabil eller BIBO stabil, om varje avgränsad ingång ger upphov till en avgränsad utgång, som

\(\displaystyle \sum_{k=0}^{\infty}\left|H(k)\right|<\infty \)

där, \(\small h(k)\) är lti-systemets impulsrespons. Analysera denna ekvation bör det vara tydligt att Bibo-stabilitetskriteriet endast kommer att uppfyllas om systemets poler ligger inuti enhetscirkeln, eftersom systemets ROC (konvergensregion) måste inkludera enhetscirkeln. Följaktligen är det tillräckligt att säga att en avgränsad ingångssignal alltid kommer att producera en avgränsad utsignal om alla poler ligger inuti enhetscirkeln.

nollorna å andra sidan begränsas inte av detta krav och kan följaktligen ligga var som helst på z-planet, eftersom de inte direkt påverkar systemstabiliteten. Därför kan en systemstabilitetsanalys utföras genom att först beräkna rötterna för överföringsfunktionen (dvs. rötterna till täljaren och nämnaren polynomier) och sedan plotta motsvarande poler och nollor på z-planet.

en intressant situation uppstår om några poler ligger på enhetscirkeln, eftersom systemet sägs vara marginellt stabilt, eftersom det varken är stabilt eller instabilt. Även om marginellt stabila system inte är BIBO-stabila, Har de utnyttjats av digitala oscillatordesigners, eftersom deras impulsrespons ger en enkel metod för att generera sinusvågor, vilket har visat sig vara ovärderligt inom telekommunikationsområdet.

Biquad IIR-filter

IIR-filterimplementeringen som diskuteras här sägs vara biquad, eftersom den har två poler och två nollor som illustreras nedan i Figur 2. Biquad-implementeringen är särskilt användbar för fastpunktsimplementeringar, eftersom effekterna av kvantisering och numerisk stabilitet minimeras. Den totala framgången för varje biquad-implementering är dock beroende av den tillgängliga talprecisionen, som måste vara tillräcklig för att säkerställa att de kvantifierade polerna alltid är inne i enhetscirkeln.

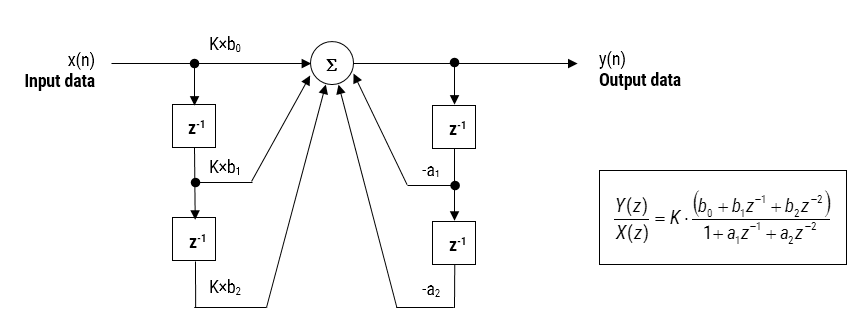
Figur 2: Direkt Form I (biquad) IIR filter förverkligande och överföringsfunktion.

genom att analysera Figur 2 kan man se att biquadstrukturen faktiskt består av två återkopplingsvägar (skalas av \(\small a_1\) och \(\small a_2\)), tre matningsvägar framåt (skalas av \(\small b_0, b_1\) och \(\small b_2\)) och en sektionsvinst, \(\small K\). Således kan filtreringsoperationen i Figur 1 sammanfattas med följande enkla rekursiva ekvation:

\(\displaystyle y (n)=K \ gånger \ Big – a_1 y (n-1) – a_2 y (n-2)\)

analysera ekvationen, Observera att biquad-implementeringen endast kräver fyra tillägg (kräver endast en ackumulator) och fem multiplikationer, som lätt kan hysas på vilken Cortex-m-mikrokontroller som helst. Sektionsförstärkningen, \(\small K\) kan också multipliceras med framåtvägskoefficienterna före implementering.

en samling Biquad-filter kallas en Biquad-kaskad, som illustreras nedan.

ASN Filter Designer kan designa och implementera en kaskad på upp till 50 biquads (endast Professional edition).

Flytpunktsimplementering

vid implementering av ett filter i flytpunkt (dvs. med dubbel eller enkel precisionsaritmetik) anses Direktform II-strukturer vara ett bättre val än Direktform i-strukturen. Den direkta Form II-transponerade strukturen anses vara den mest numeriskt korrekta för flytpunktsimplementering, eftersom de oönskade effekterna av numerisk swamping minimeras, vilket ses genom att analysera skillnadsekvationerna.

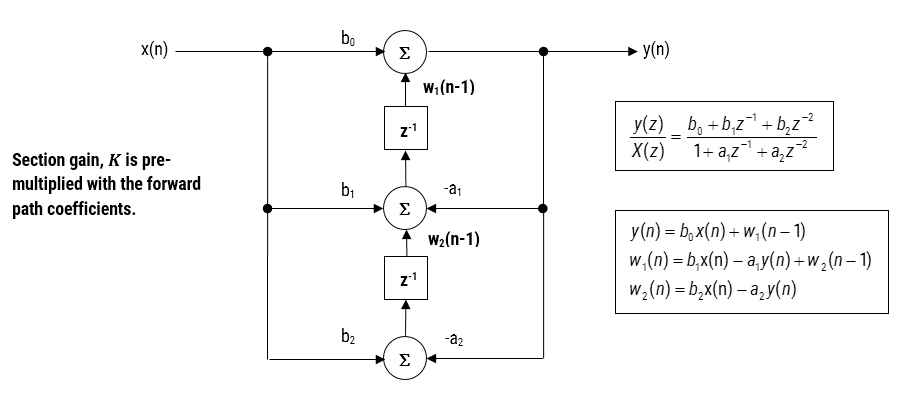
direct Form II transponerade strucutre, överföringsfunktion och differensekvationer; IIR filter; Biquad Filter

Figur 3-Direct Form II transponerade strucutre, överföringsfunktion och differensekvationer

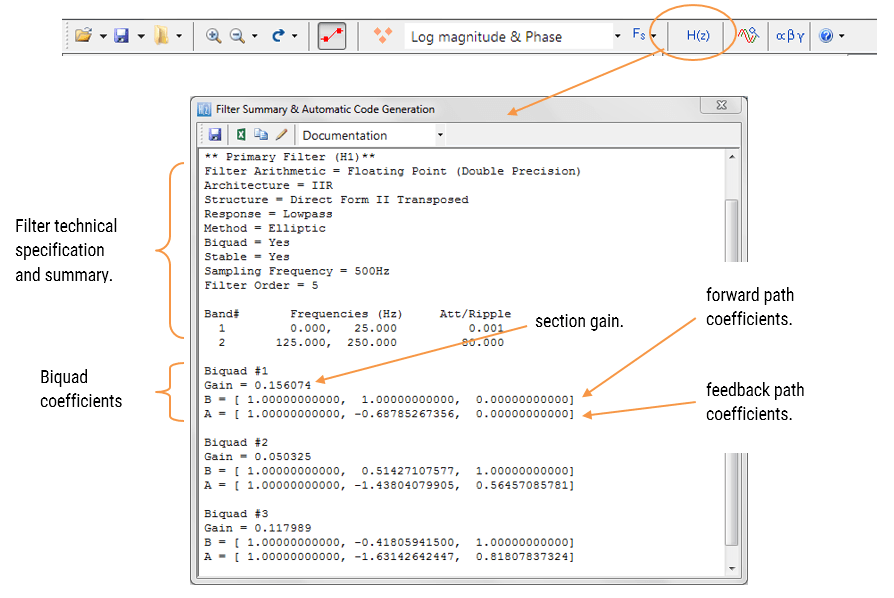
filteröversikten (visas i Figur 4) ger designern en detaljerad översikt över det designade filtret, inklusive en detaljerad sammanfattning av de tekniska specifikationerna och filterkoefficienterna, som ger en snabb och enkel väg att dokumentera din design.

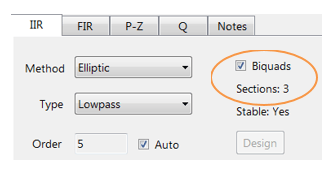
ASN – Filterdesignern stöder design och implementering av både enstaka avsnitt och biquad (standardinställning) IIR-filter.

Figur 4: detaljerad specifikation.

fir-definition

returnerar IIR: s linjära konstanta koefficientdifferensekvation, dvs

\(\displaystyle
y (n)= \ sum_{k = 0}^{q}b_kx (n-k)- \ sum_{k=1}^{p}a_ky(n-k)
\)

Lägg märke till att när vi ställer in \(\small a_k\) koefficienterna (dvs återkopplingen) till noll, minskar definitionen till vår ursprungliga FIR – filterdefinitionen, vilket innebär att fir-beräkningen bara är baserad på tidigare och nuvarande ingångsvärden, nämligen:

\(\displaystyle
y (n)= \ sum_{k = 0}^{q}b_kx (n-k)
\)

implementering

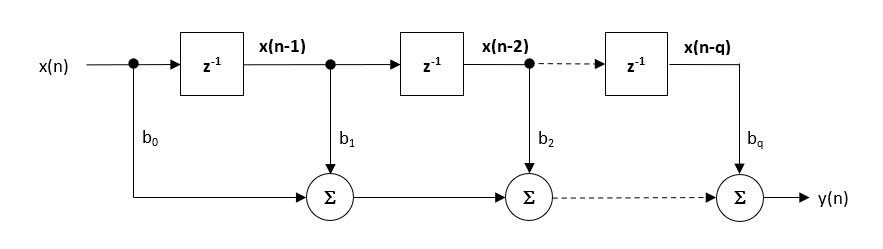
även om flera praktiska implementeringar för Gran finns, är den direkta formstrukturen och dess transponerade kusin kanske den vanligaste, och som sådan är alla utformade filterkoefficienter avsedda för implementering i en direkt formstruktur.

den direkta formstrukturen och tillhörande skillnadsekvation visas nedan. Den direkta formen förespråkas för implementering av fast punkt på grund av konceptet med en enda ackumulator.

\(\displaystyle y(n) = b_0x(n) + b_1x (n-1) + b_2x (n-2)+…. + b_qx (n-q) \)

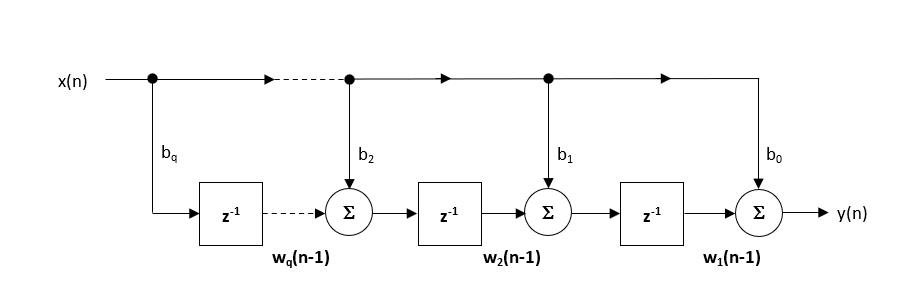
den rekommenderade (standard) strukturen inom ASN-Filterdesignern är den direkta formen transponerade strukturen, eftersom detta ger överlägsen numerisk noggrannhet vid användning av flytpunkt aritmetik. Detta kan lätt ses genom att analysera skillnadsekvationerna nedan (används för implementering), eftersom de oönskade effekterna av numerisk swamping minimeras, eftersom flytpunktsaddition utförs på antal av liknande storlek.

\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \Quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)

Vad har vi lärt oss?