Zlomky, Procenta a Poměry Části: Modely pro Násobení a Dělení Zlomků (45 minut)

BY admin
|

V Této Části: Oblast Modelu pro Násobení
V minulosti, možná jste se dozvěděli konkrétní algoritmy pro násobení a dělení zlomků. Nyní budeme používat některé z vizuálních modelů jsme zaměstnaných dříve v tomto kurzu, aby lépe pochopit, co se vlastně děje, když jsme se provádět tyto operace. Viz Poznámka 2 níže.

První použijeme oblasti model — ten, který překryje čtverců, které jsou rozděleny do vhodných počet oblastí, a ve stínu, jak je potřeba — objasnit, co se stane, když násobíte zlomky. Například, tady je návod, jak bychom použít oblast modelu demonstrovat problém 3/8 • 2/3:

Odstín jeden metr, rozdělený vertikálně, představují 3/8 (uvedeno níže v růžové): Odstín další čtverec, rozdělený horizontálně, představují 2/3 (uvedeno níže v modré): Překrýt dva čtverce. Výrobek je oblast, která je dvojí-shaded (uvedeno níže v fialová):

Jaká je hodnota této fialové oblasti? Existují 3 * 2, nebo 6, fialové části z 8 * 3, nebo 24, díly ve všech, takže hodnota fialové oblasti je 6/24.

tento model vizuálně demonstruje známý algoritmus: vynásobte dvě frakce, vynásobte čitatele a poté vynásobte jmenovatele. Tento algoritmus „počítá“ jak fialové části (produkt dvou čitatelů), tak celkový počet částí (produkt dvou jmenovatelů).

tento model můžeme také použít k „zmenšení“ zlomku. Nejprve zaměníme pozice některých fialových částí. Dvě z fialových částí lze přesunout na vrchol, a tak jsou dvě z osmin nyní zastíněny. Tyto dvě osminy jsou stejné oblasti jako jednoho čtvrtletí:

V Této Části: Zkuste si To Sami
vytvořte si vlastní metr fólie překrýt, a modelu řešení pro každý krok v řešení A1 níže.

problém A1
letecká fotografie zemědělské půdy ukazuje rozměry tří polí ve zlomcích míle. Použití oblast modelu právě jste se naučili modelovat prostor v čtverečních kilometrů z každé z těchto polí:
. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

Problém A2
Popsat jak oblast modelu ukazuje, že součin dvou kladných zlomků, každý méně než 1, musí být menší, než některou z frakcí.

Video Segment
V tomto segmentu, Jeanne a Liz použít oblast modelu násobit zlomky. Vztahují tento model k multiplikačnímu algoritmu a kontrolují způsoby, jak vizuálně snížit zlomky. Podívejte se na tento segment videa po dokončení problémů A1 a A2.

tento segment najdete na videu relace přibližně 4 minuty a 32 sekund po logu Annenberg Media.

V Této Části: Oblast Modelu pro Rozdělení
můžeme použít oblast modelu pro násobení zlomků vizualizovat rozdělení na dvě frakce, kdy každá je menší než 1. Pro modelování dělení zlomky více či méně zvrátíme proces používaný pro násobení. Začneme oblastí, kterou hledáme, a najdeme jeden z chybějících faktorů, který tuto oblast tvoří. Viz Poznámka 3 níže.

například, tady je návod, jak bychom použít model demonstruje problém 1/4 2/3:

Odstín jeden metr, rozdělený vertikálně, představovat 1/4 (stejně jako v násobení model, stínovaný fialová): Překrýt čtverec rozdělen na třetiny, umístěné vodorovně, na čtvrtiny náměstí, a nakreslit držák do rohu třetiny náměstí ukázat velikost 2/3:

to, Co vidíte teď je fialová (1/4) oblast a velikost jedním z faktorů, které z této oblasti.

z multiplikačního modelu víme, že součin 2/3 a jiného faktoru (kvocientu) definuje plochu ekvivalentní velikosti 1/4. Abychom našli kvocient, musíme přesunout horní část fialové oblasti tak, aby měla stejnou výšku jako faktor 2/3.

rozdělte čtvrtiny náměstí, aby se osminy náměstí: Pohyb horní dva fialové kousky do 2/3 výšky oblasti (oblast, ve 2/3 držák): Nyní odstín obdélníky ihned na přímo a bezprostředně nad fialové oblasti:

To ukazuje, že tam jsou 3 • 2, nebo 6, fialová díly z 8 • 3, nebo 24, díly v. Fialová oblast se rovná 1/4 a pochází z produktu 2/3 vynásobeného čím? Vidíme, že druhý faktor je 3/8.

problém A3
město plánuje vybudovat komunitní zahradu, která pokryje 2/3 kilometru čtverečního. Chtěli by ji umístit na pastvinu staré koňské farmy. Jeden rozměr zahradní plochy bude určen plotem, který je 3/4 míle dlouhý. Použijte model plochy pro rozdělení k určení další dimenze NOVÉ zahradní plochy.

problém A4
popište, jak model plochy ukazuje, že kvocient dvou kladných frakcí, každá menší než 1, musí být větší než první zlomek.

V Této Části: Model společného jmenovatele pro dělení
model plochy pro dělení zlomků nepomáhá ilustrovat, proč algoritmus, který jsme nejvíce obeznámeni s (Invertovat dělitel a pak násobit) funguje. Bohužel to žádný model nemůže ukázat. Viz Poznámka 4 níže.

ale zde je jiný algoritmus dělení, který můžeme vysvětlit pomocí modelu: Najděte společného jmenovatele, najděte ekvivalentní zlomky a rozdělte čitatele.

abychom porozuměli modelu tohoto algoritmu, pojďme se nejprve vrátit k přezkoumání některých pojmů dělení. Obvykle je snazší vypočítat, pokud přemýšlíte o rozdělení citativním způsobem. Můžete tedy říci, že 6 3 se ptá: „Kolik 3 je v 6?“

dále musíme pochopit roli jednotek v divizi.

problém A5
který, pokud existuje, z těchto otázek dává jinou odpověď?
* kolik 3s je v 6?
* kolik skupin po 3 desítkách je v 6 desítkách?
* kolik skupin po 3 pětkách je v 6 pětkách?
* kolik skupin po 3 desetinách je v 6 desetinách?* Kolik skupin 3 @s je v 6 @s?
* kolik skupin po 3 anythings je v 6 anythings (pokud obě anythings odkazují na stejnou jednotku)?

jde o to, že na jednotkách problému nezáleží — pokud jsou jednotky stejnou entitou, zmizí, když se rozdělíte.

to nás přivádí zpět k novému algoritmu pro dělení zlomky: rozdělit dvě zlomky, najít společného jmenovatele a pak rozdělit čitatele.

zkusme vizuální verzi problému, který jsme udělali dříve: 1/4 2/3. Nejprve najděte společného jmenovatele:

1/4 2/3 = 3/12 8/12

Dále, rozdělit čitatele:

38 = 3/8

Zde je model pro tento problém, se nazývá společný jmenovatel model:

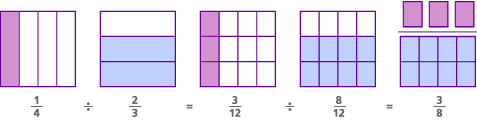
V tomto problému, ve skutečnosti, původní otázka byla „Kolik je 2/3s jsou tam v 1/4?“Nalezením společného jmenovatele jsme změnili otázku na“ kolik 8 / 12 je v 3/12?“- což je stejné jako ptát se “ kolik 8s je ve 3?“Odpověď na obě otázky je stejná :“ existuje 3/8 8 v 3.“

problém A6
použijte společný jmenovatel pro vydělení 3/5 3/4.

problém A7
proč má 0.6 0.2 stejnou odpověď jako 6 2?

v této části: převedení procesu na desetinná místa
můžete rozšířit to, co jste se dozvěděli o operacích a zlomcích, také na desetinná místa. Nezapomeňte, že končící desetinné číslo může být považováno za zlomek s výkonem 10 jako jmenovatel (např. 0,4 = 4/10). Viz poznámka 5 níže.

proč potřebujeme zarovnat desetinná místa, když sčítáme nebo odečítáme desetinná místa?
musíme zarovnat desetinná místa, protože můžeme sčítat nebo odečítat pouze v případě, že jednotky jsou stejné. Zarovnáním desetinných míst se ujistíme, že přidáváme nebo odečítáme číslice, které mají stejné hodnoty místa, stejně jako když přidáváme nebo odečítáme celá čísla.

proč počítáme desetinná místa, když vynásobíme desetinná místa?
z části o exponentech v relaci 3 víme, že násobení exponenty vyžaduje přidání nebo“ počítání “ exponentů. Takže například 0,2 * 0,03 v exponenciální podobě je následující:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

exponenty jsou -1 a -2, což jsou jedno a dvě místa napravo od desetinné tečky. Produkt pak bude mít exponent, který je součtem -1 a -2 (tj. -3) a je tři místa napravo od desetinné tečky. Produkt 0.2 * 0.03 je 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

proč při dělení desetinnými místy přesouváme desetinná místa?
tento proces souvisí s nalezením ekvivalentních frakcí. Můžete si představit rozdělení jako zlomek. Od problému 2.5 0.05 je těžké si představit, napište jej jako 2,5 / 0,05. Ve jmenovateli potřebujete celé číslo, takže vynásobte 100, abyste získali celé číslo. Chcete-li kompenzovat vynásobení jmenovatele 100, musíte také vynásobit čitatel 100. To znamená, že jste vlastně vynásobili 100/100, nebo 1, což nemění hodnotu zlomku. Zde je to, co proces vypadá: