Fractions, Pourcentages et Ratios Partie A: Modèles pour la Multiplication et la Division des Fractions (45 minutes)

BY admin
|

Dans Cette Partie: Modèle d’aire pour la Multiplication
Dans le passé, vous avez peut-être appris des algorithmes particuliers pour la multiplication et la division des fractions. Nous allons maintenant utiliser certains des modèles visuels que nous avons utilisés plus tôt dans ce cours pour mieux comprendre ce qui se passe réellement lorsque nous effectuons ces opérations. Voir la note 2 ci-dessous.

Tout d’abord, nous utiliserons un modèle d’aire — un modèle qui superpose des carrés qui sont partitionnés en un nombre approprié de régions et ombrés au besoin — pour clarifier ce qui se passe lorsque vous multipliez des fractions. Par exemple, voici comment nous utiliserions le modèle de zone pour démontrer le problème 3/8 • 2/3:

Abat-jour un carré, partitionné verticalement, pour représenter 3/8 (illustré ci-dessous en rose): Ombrez un autre carré, partitionné horizontalement, pour représenter les 2/3 (illustré ci-dessous en bleu): Superposez les deux carrés. Le produit est la zone à double ombrage (indiquée ci-dessous en violet):

Quelle est la valeur de cette zone violette? Il y a 3 * 2, ou 6, parties violettes sur 8 * 3, ou 24, parties en tout, donc la valeur de la zone violette est de 6/24.

Ce modèle démontre visuellement l’algorithme familier: multiplier deux fractions, multiplier les numérateurs puis multiplier les dénominateurs. Cet algorithme « compte » à la fois les parties violettes (le produit des deux numérateurs) et le nombre total de parties (le produit des deux dénominateurs).

Nous pouvons également utiliser ce modèle pour « réduire » la fraction. D’abord, nous échangeons les positions de certaines des parties violettes. Deux des parties violettes peuvent être déplacées vers le haut, et ainsi, deux des huitièmes sont maintenant ombrées. Ces deux huitièmes sont la même surface qu’un quart:

Dans cette partie: Essayez-le vous-même
Faites vos propres transparences carrées à superposer, et modélisez la solution pour chaque étape du problème A1 ci-dessous.

Problème A1
Une photo aérienne de terres agricoles montre les dimensions de trois champs en fractions de mille. Utilisez le modèle de zone que vous venez d’apprendre pour modéliser la zone en miles carrés de chacun de ces champs:
a. 3/4 • 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

Problème A2
Décrivez comment le modèle d’aire montre que le produit de deux fractions positives, chacune inférieure à 1, doit être plus petit que l’une ou l’autre des fractions.

Segment vidéo
Dans ce segment, Jeanne et Liz utilisent le modèle d’aire pour multiplier les fractions. Ils relient ce modèle à l’algorithme de multiplication et vérifient les moyens de réduire visuellement les fractions. Regardez ce segment vidéo après avoir terminé les problèmes A1 et A2.

Vous pouvez trouver ce segment sur la vidéo de la session environ 4 minutes et 32 secondes après le logo Annenberg Media.

Dans Cette partie : Modèle d’aire pour la Division
Nous pouvons appliquer le modèle d’aire pour la multiplication des fractions pour visualiser la division de deux fractions lorsque chacune est inférieure à 1. Pour modéliser la division avec des fractions, nous inversons plus ou moins le processus utilisé pour la multiplication. Nous commençons par une zone que nous recherchons, et nous trouvons l’un des facteurs manquants qui composent cette zone. Voir la note 3 ci-dessous.

Par exemple, voici comment nous utiliserions le modèle pour démontrer le problème 1/4 2/3:

Ombrez un carré, partitionné verticalement, pour représenter 1/4 (comme dans le modèle de multiplication, il est ombré de violet): Superposez un carré partitionné en tiers, positionné horizontalement, sur le carré des quarts, et dessinez une parenthèse à droite du carré des tiers pour montrer la taille des 2/3:

Ce que vous voyez maintenant, c’est la zone violette (1/4) et la taille de l’un des facteurs qui ont fait cette zone.

Nous savons d’après le modèle de multiplication que le produit de 2/3 et d’un autre facteur (le quotient) définit une surface de taille équivalente à 1/4. Pour trouver le quotient, nous devons déplacer la partie supérieure de la zone violette pour qu’elle ait la même hauteur que le facteur 2/3.

Subdiviser le carré des quarts pour faire un carré des huitièmes: Déplacez les deux pièces violettes supérieures dans la zone de hauteur 2/3 (la zone dans le support 2/3): Maintenant, ombrez les rectangles immédiatement à droite et immédiatement au-dessus de la zone violette:

Cela montre qu’il y a 3 • 2, ou 6, parties violettes sur 8 • 3, ou 24, parties en tout. La zone violette est égale à 1/4, et elle provient du produit de 2/3 multiplié par quoi? Nous pouvons voir que l’autre facteur est de 3/8.

Problème A3
Une ville prévoit de construire un jardin communautaire qui couvrira 2/3 d’un mille carré. Ils aimeraient le situer sur un pâturage d’une ancienne ferme équestre. Une dimension du jardin sera déterminée par une clôture de 3/4 de mille de long. Utilisez le modèle de zone de division pour déterminer l’autre dimension de la nouvelle zone de jardin.

Problème A4
Décrivez comment le modèle d’aire montre que le quotient de deux fractions positives, chacune inférieure à 1, doit être supérieur à la première fraction.

Dans Cette Partie: Le modèle de dénominateur commun pour la division
Le modèle d’aire pour la division des fractions n’aide pas à illustrer pourquoi l’algorithme que nous connaissons le mieux (inverser le diviseur puis multiplier) fonctionne. Malheureusement, aucun modèle ne peut le montrer. Voir la Note 4 ci-dessous.

Mais voici un algorithme de division différent, que nous pouvons expliquer avec un modèle: Trouver le dénominateur commun, trouver les fractions équivalentes et diviser les numérateurs.

Afin de comprendre le modèle de cet algorithme, revenons d’abord sur certains concepts de division. Il est généralement plus facile à calculer si vous pensez à la division de manière quotative. Ainsi, vous pouvez dire que 6 3 demande: « Combien y a-t-il de 3 dans 6? »

Ensuite, nous devons comprendre le rôle des unités dans la division.

Problème A5
Laquelle, le cas échéant, de ces questions donne une réponse différente?

Le point ici est que les unités du problème n’ont pas d’importance — si les unités sont la même entité, elles disparaissent lorsque vous divisez.

Cela nous ramène au nouvel algorithme de division par fractions : diviser deux fractions, trouver un dénominateur commun puis diviser les numérateurs.

Essayons une version visuelle du problème que nous avons rencontré auparavant: 1/4 2/3. Tout d’abord, trouvez un dénominateur commun:

1/4 2/3 = 3/12 8/12

Ensuite, divisez les numérateurs:

38 = 3/8

Voici le modèle de ce problème, appelé modèle du dénominateur commun:

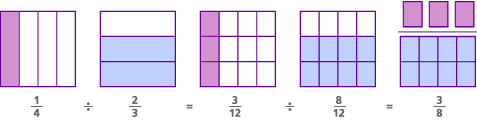
Dans ce problème, en effet, la question initiale était « Combien y a-t-il de 2 / 3 en 1/4? »En trouvant un dénominateur commun, nous avons changé la question en « Combien y a-t-il de 8 / 12 en 3/12?— – ce qui revient à demander « Combien y a-t-il de 8 en 3? »La réponse aux deux questions est la même: « Il y a 3/8 d’un 8 en 3. »

Problème A6
Utilisez le modèle du dénominateur commun pour diviser 3/5 par 3/4.

Problème A7
Pourquoi 0.6 0.2 a-t-il la même réponse que 6 2?

Dans cette partie: Traduire le processus en Décimales
, vous pouvez également étendre ce que vous avez appris sur les opérations et les fractions aux décimales. Rappelez-vous qu’une décimale terminale peut être considérée comme une fraction avec une puissance de 10 comme dénominateur (par exemple, 0,4 = 4/10). Voir la note 5 ci-dessous.

Pourquoi devons-nous aligner les décimales lorsque nous ajoutons ou soustrayons des décimales?
Nous devons aligner les décimales car nous ne pouvons ajouter ou soustraire que si les unités sont les mêmes. En alignant les décimales, nous nous assurons que nous ajoutons ou soustrayons des chiffres qui ont les mêmes valeurs de lieu, tout comme nous le faisons lorsque nous ajoutons ou soustrayons des nombres entiers.

Pourquoi comptons-nous les décimales lorsque nous multiplions les décimales?
De la section sur les exposants de la session 3, nous savons que la multiplication avec des exposants nécessite d’ajouter, ou de « compter », les exposants. Ainsi, par exemple, 0,2 * 0,03 sous la forme exponentielle est la suivante:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

Les exposants sont -1 et -2, qui sont respectivement un et deux endroits à droite de la virgule décimale. Le produit aura alors un exposant qui est la somme de -1 et -2 (c’est-à-dire, -3), et est à trois endroits à droite de la virgule décimale. Le produit de 0,2 * 0,03 est 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

Pourquoi déplace-t-on les points décimaux lors de la division par des décimales?
Ce processus est lié à la recherche de fractions équivalentes. Vous pouvez considérer la division comme une fraction. Depuis le problème 2.5 0.05 est difficile à visualiser, écrivez-le comme 2.5 / 0.05. Vous avez besoin d’un nombre entier dans le dénominateur, alors multipliez par 100 pour obtenir un nombre entier. Pour compenser la multiplication du dénominateur par 100, vous devez également multiplier le numérateur par 100. Cela signifie que vous avez effectivement multiplié par 100/100, ou 1, ce qui ne change pas la valeur de la fraction. Voici à quoi ressemble le processus: