fracties, percenten en verhoudingen deel A: modellen voor de vermenigvuldiging en deling van fracties (45 minuten)

in dit deel: Gebiedsmodel voor vermenigvuldiging
in het verleden hebt u wellicht bepaalde algoritmen voor de vermenigvuldiging en deling van fracties geleerd. We gaan nu enkele van de visuele modellen gebruiken die we eerder in deze cursus hebben gebruikt om beter te begrijpen wat er werkelijk gebeurt wanneer we deze bewerkingen uitvoeren. Zie noot 2 hieronder.

eerst zullen we een gebiedsmodel gebruiken — Een dat vierkantjes over elkaar legt die verdeeld zijn in het juiste aantal regio ‘ s, en waar nodig gearceerd wordt — om te verduidelijken wat er gebeurt als je breuken vermenigvuldigt. Bijvoorbeeld, hier is hoe zouden we gebruik maken van de model aan te tonen van het probleem 3/8 • 2/3:

Schaduw, een vierkant, verdeeld verticaal, te vertegenwoordigen 3/8 (hieronder weergegeven in roze):		Schaduw een vierkant, verdeeld horizontaal, te vertegenwoordigen 2/3 (hieronder weergegeven in blauw):		Overlappen de twee pleinen. Het product is het gebied dat is Dubbel-Gearceerd (hieronder weergegeven in paars):

Wat is de waarde van dit paarse gebied? Er zijn 3 • 2, of 6, paarse delen van 8 * 3, of 24, delen in totaal, dus de waarde van het paarse gebied is 6/24.

dit model toont visueel het bekende algoritme: om twee breuken te vermenigvuldigen, vermenigvuldigt u de tellers en vermenigvuldigt u vervolgens de noemers. Dit algoritme “telt” zowel de paarse delen (het product van de twee tellers) en het totale aantal delen (het product van de twee noemers).

we kunnen dit model ook gebruiken om de breuk te” verminderen”. Eerst wisselen we de posities van enkele paarse delen. Twee van de paarse delen kunnen naar de top worden verplaatst, en dus zijn twee van de achtsten nu gearceerd. Deze twee achtsten zijn hetzelfde gebied als een kwart:

in dit deel: Probeer het zelf
maak uw eigen vierkante transparanten om over elkaar te leggen, en modelleer de oplossing voor elke stap in probleem A1 hieronder.

probleem A1
een luchtfoto van landbouwgrond toont de afmetingen van drie velden in fracties van een mijl. Gebruik het gebiedsmodel dat u zojuist hebt geleerd om het gebied in vierkante mijlen van elk van deze velden te modelleren:
a. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

opgave A2
beschrijf hoe het oppervlaktemodel aantoont dat het product van twee positieve fracties, elk kleiner dan 1, kleiner moet zijn dan een van de fracties.

Video Segment
in dit segment gebruiken Jeanne en Liz het area model om breuken te vermenigvuldigen. Ze relateren dit model aan het vermenigvuldigingsalgoritme en controleren op manieren om breuken visueel te verminderen. Bekijk dit videosegment nadat u de problemen A1 en A2 hebt voltooid.

u vindt dit segment op de sessievideo ongeveer 4 minuten en 32 seconden na het Annenberg Media-logo.

in dit deel: Area Model voor deling
kunnen we het area model voor de vermenigvuldiging van fracties toepassen om de verdeling van twee fracties te visualiseren wanneer elk kleiner is dan 1. Om deling met breuken te modelleren, keren we het proces dat Voor vermenigvuldiging wordt gebruikt min of meer om. We beginnen met een gebied dat we zoeken, en we vinden een van de ontbrekende factoren die dat gebied uitmaken. Zie Noot 3 hieronder.

bijvoorbeeld, hier is hoe we het model zouden gebruiken om het probleem aan te tonen 1/4 2/3:

schaduw een vierkant, verticaal verdeeld, om 1/4 weer te geven (zoals in het vermenigvuldigingsmodel, het is gearceerd paars):		leg een vierkant verdeeld in derden, horizontaal gepositioneerd, op het vierden vierkant, en teken een Beugel Rechts van het derde vierkant om de grootte van 2/3 te tonen:

wat je nu ziet is het paarse (1/4) gebied en de grootte van een van de factoren die dat gebied maakte.

uit het vermenigvuldigingsmodel weten we dat het product van 2/3 en een andere factor (het quotiënt) een oppervlakte definieert die in grootte gelijk is aan 1/4. Om het quotiënt te vinden, moeten we het bovenste deel van het paarse gebied verplaatsen zodat het dezelfde hoogte is als de 2/3 factor.

verdeel het vierden vierkant om een achtsten vierkant te maken:		Verplaats de bovenste twee paarse stukken in de 2/3 hoogte area (het gebied binnen de 2/3 beugel):		Nu de schaduw van de rechthoeken onmiddellijk naar rechts en direct boven het paarse gebied:

Dit toont aan dat er 3 • 2 of 6, de paarse delen van de 8 • 3, of 24, delen in alles. Het paarse gebied is gelijk aan 1/4, en het kwam van het product van 2/3 vermenigvuldigd met wat? We kunnen zien dat de andere factor 3/8 is.

probleem A3
een stad is van plan een gemeenschappelijke tuin te bouwen die 2/3 van een vierkante mijl zal beslaan. Ze willen het op een weiland van een oude paardenboerderij plaatsen. Een dimensie van de tuin wordt bepaald door een hek dat is 3/4 van een mijl lang. Gebruik het gebiedsmodel voor verdeling om de andere dimensie van de nieuwe tuin te bepalen.

opgave A4
beschrijf hoe het oppervlaktemodel aantoont dat het quotiënt van twee positieve fracties, elk kleiner dan 1, groter moet zijn dan de eerste fractie.

In Dit Deel: Het gemeenschappelijke Noemermodel voor deling
het oppervlaktemodel voor de deling van breuken helpt niet om te illustreren waarom het algoritme waarmee we het meest vertrouwd zijn (de deler omkeren en dan vermenigvuldigen) werkt. Helaas kan geen enkel model dat aantonen. Zie Noot 4 hieronder.

maar hier is een ander deelalgoritme, een dat we met een model kunnen verklaren: Zoek de gemeenschappelijke noemer, zoek de equivalente breuken en deel de tellers.

om het model voor dit algoritme te begrijpen, gaan we eerst terug naar enkele concepten van deling. Het is meestal makkelijker om te berekenen als je op een quotatieve manier over deling denkt. Dus kun je zeggen dat 6 3 vraagt: “hoeveel 3′ s zijn er in 6?”

vervolgens moeten we de rol van eenheden in deling begrijpen.

probleem A5
welke van deze vragen geeft een ander antwoord?
* hoeveel 3 ‘ s zijn er in 6?
* hoeveel groepen van 3 TEN ’s zijn er in 6 TEN’ s?
* hoeveel groepen van 3 vijven zijn er in 6 vijven?
* hoeveel groepen van 3 tienden zijn er in 6 tienden?* Hoeveel groepen van 3 @s zijn er in 6 @s?
* hoeveel groepen van 3 anythings zijn er in 6 anythings (zolang beide anythings verwijzen naar dezelfde eenheid)?

het punt is dat de eenheden van het probleem er niet toe doen-als de eenheden dezelfde entiteit zijn, verdwijnen ze wanneer je deelt.

dit brengt ons terug naar het nieuwe algoritme voor deling met breuken: om twee breuken te delen, vindt u een gemeenschappelijke noemer en deelt u de tellers.

laten we een visuele versie proberen van het probleem dat we eerder deden: 1/4 2/3. Zoek eerst een gemeenschappelijke noemer:

1/4 2/3 = 3/12 8/12

deel vervolgens de tellers:

38 = 3/8

hier is het model voor dit probleem, het zogenaamde gemeenschappelijke noemermodel:

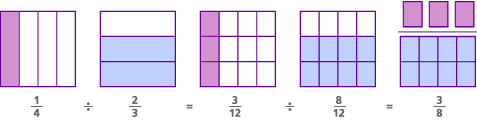
In dit probleem, in feite, de oorspronkelijke vraag was ” hoeveel 2 / 3s zijn er in 1/4?”Door een gemeenschappelijke noemer te vinden, hebben we de vraag veranderd in “hoeveel 8/12s zijn er in 3/12?”- wat hetzelfde is als vragen ” hoeveel 8s zijn er in 3?”Het antwoord op beide vragen is hetzelfde:” er is 3/8 van een 8 in 3.”

probleem A6
gebruik het model van de gemeenschappelijke noemer om 3/5 door 3/4 te delen.

probleem A7
Waarom heeft 0,6 0,2 hetzelfde antwoord als 6 2?

in dit deel: het vertalen van het proces naar decimalen
kunt u wat u hebt geleerd over operaties en fracties ook uitbreiden naar decimalen. Vergeet niet dat een decimaal kan worden beschouwd als een breuk met een macht van 10 als de noemer (bijvoorbeeld, 0.4 = 4/10). Zie noot 5 hieronder.

Waarom moeten we de decimalen op een rij zetten als we decimalen optellen of aftrekken?
we moeten de decimalen op een rij zetten omdat we alleen kunnen optellen of aftrekken als de eenheden hetzelfde zijn. Door de decimale punten uit te lijnen, zorgen we ervoor dat we cijfers toevoegen of aftrekken die dezelfde plaatswaarden hebben, net zoals we doen wanneer we hele getallen optellen of aftrekken.

waarom tellen we de decimalen als we decimalen vermenigvuldigen?
uit de sectie over exponenten in Sessie 3 weten we dat vermenigvuldiging met exponenten het toevoegen of “tellen” van de exponenten vereist. Dus, bijvoorbeeld, 0,2 * 0,03 in de exponentiële vorm is de volgende:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

de exponenten zijn -1 en -2, die respectievelijk één en twee plaatsen rechts van de komma zijn. Het product zal dan een exponent hebben die de som is van -1 en -2 (d.w.z. -3), en is drie plaatsen rechts van de komma. Het product van 0.2 * 0.03 is 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

waarom verplaatsen we de decimalen bij het delen met decimalen?
dit proces houdt verband met het vinden van gelijkwaardige breuken. Je kunt de verdeling zien als een breuk. Sinds het probleem 2.5 0.05 is moeilijk te visualiseren, schrijf het als 2.5 / 0.05. Je hebt een heel getal nodig in de noemer, dus vermenigvuldig met 100 om een heel getal te krijgen. Om het vermenigvuldigen van de noemer met 100 te compenseren, moet je ook de teller met 100 vermenigvuldigen. Dat betekent dat je eigenlijk vermenigvuldigd met 100/100, of 1, Wat de waarde van de breuk niet verandert. Zo ziet het proces eruit: