Brüche, Prozente und Verhältnisse Teil A: Modelle zur Multiplikation und Division von Brüchen (45 Minuten)

BY admin
|

In diesem Teil: Flächenmodell zur Multiplikation
In der Vergangenheit haben Sie möglicherweise bestimmte Algorithmen zur Multiplikation und Division von Brüchen gelernt. Wir werden nun einige der visuellen Modelle verwenden, die wir zuvor in diesem Kurs verwendet haben, um besser zu verstehen, was tatsächlich passiert, wenn wir diese Operationen ausführen. Siehe Anmerkung 2 unten.

Zunächst verwenden wir ein Flächenmodell — eines, das Quadrate überlagert, die in die entsprechende Anzahl von Regionen unterteilt und nach Bedarf schattiert sind —, um zu klären, was passiert, wenn Sie Brüche multiplizieren. So würden wir beispielsweise das Flächenmodell verwenden, um das Problem zu demonstrieren 3/8 • 2/3:

Schattieren Sie ein vertikal partitioniertes Quadrat, um 3/8 darzustellen (siehe unten in Rosa): Schattieren Sie ein weiteres horizontal partitioniertes Quadrat, um 2/3 darzustellen (siehe unten in Blau): Überlagern Sie die beiden Quadrate. Das Produkt ist der Bereich, der doppelt schattiert ist (unten in lila dargestellt):

Was ist der Wert dieses lila Bereichs? Es gibt 3 • 2 oder 6 violette Teile von insgesamt 8 • 3 oder 24 Teilen, sodass der Wert des violetten Bereichs 6/24 beträgt.

Dieses Modell demonstriert visuell den bekannten Algorithmus: Um zwei Brüche zu multiplizieren, multiplizieren Sie die Zähler und multiplizieren Sie dann die Nenner. Dieser Algorithmus „zählt“ sowohl die violetten Teile (das Produkt der beiden Zähler) als auch die Gesamtzahl der Teile (das Produkt der beiden Nenner).

Wir können dieses Modell auch verwenden, um den Bruch zu „reduzieren“. Zuerst tauschen wir die Positionen einiger der violetten Teile aus. Zwei der violetten Teile können nach oben verschoben werden, und somit sind zwei der Achtel jetzt schattiert. Diese beiden Achtel sind die gleiche Fläche wie ein Viertel:

In diesem Teil: Probieren Sie es selbst aus
Erstellen Sie Ihre eigenen quadratischen Transparenzen zum Überlagern und modellieren Sie die Lösung für jeden Schritt in Problem A1 unten.

Problem A1
Ein Luftbild von Ackerland zeigt die Dimensionen von drei Feldern in Bruchteilen einer Meile. Verwenden Sie das Flächenmodell, das Sie gerade gelernt haben, um die Fläche in Quadratmeilen jedes dieser Felder zu modellieren:
a. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

Problem A2
Beschreiben Sie, wie das Flächenmodell zeigt, dass das Produkt zweier positiver Fraktionen, die jeweils kleiner als 1 sind, kleiner sein muss als eine der Fraktionen.

Videosegment
In diesem Segment verwenden Jeanne und Liz das Flächenmodell, um Brüche zu multiplizieren. Sie beziehen dieses Modell auf den Multiplikationsalgorithmus und suchen nach Möglichkeiten, Brüche visuell zu reduzieren. Sehen Sie sich dieses Videosegment an, nachdem Sie die Probleme A1 und A2 gelöst haben.

Dieses Segment finden Sie auf dem Session-Video ca. 4 Minuten und 32 Sekunden nach dem Annenberg Media Logo.

In diesem Teil: Flächenmodell für die Division
Wir können das Flächenmodell für die Multiplikation von Brüchen anwenden, um die Division von zwei Brüchen zu visualisieren, wenn jeder kleiner als 1 ist. Um die Division mit Brüchen zu modellieren, kehren wir den für die Multiplikation verwendeten Prozess mehr oder weniger um. Wir beginnen mit einem Bereich, den wir suchen, und wir finden einen der fehlenden Faktoren, die diesen Bereich ausmachen. Siehe Anmerkung 3 unten.

So würden wir beispielsweise das Modell verwenden, um das Problem zu demonstrieren 1/4 2/3:

Schattieren Sie ein vertikal partitioniertes Quadrat, um 1/4 darzustellen (wie im Multiplikationsmodell ist es lila schattiert): Überlagern Sie ein in Drittel unterteiltes, horizontal positioniertes Quadrat auf das Viertelquadrat und zeichnen Sie eine Klammer rechts vom Drittel-Quadrat, um die Größe von 2/3 anzuzeigen:

Was Sie jetzt sehen, ist der violette (1/4) Bereich und die Größe eines der Faktoren, die diesen Bereich gebildet haben.

Wir wissen aus dem Multiplikationsmodell, dass das Produkt aus 2/3 und einem anderen Faktor (dem Quotienten) eine Fläche definiert, deren Größe 1/4 entspricht. Um den Quotienten zu finden, müssen wir den oberen Teil des violetten Bereichs so verschieben, dass er die gleiche Höhe wie der 2/3-Faktor hat.

Unterteilen Sie das Viertelquadrat, um ein Achtel-Quadrat zu erhalten: Bewegen Sie die beiden oberen lila Stücke in den 2/3 Höhenbereich (der Bereich innerhalb der 2/3 Klammer): Schattieren Sie nun die Rechtecke sofort rechts und unmittelbar über dem violetten Bereich:

Dies zeigt, dass es 3 • 2 oder 6 lila Teile von insgesamt 8 • 3 oder 24 Teilen gibt. Die violette Fläche entspricht 1/4 und stammt aus dem Produkt von 2/3 multipliziert mit was? Wir können sehen, dass der andere Faktor 3/8 ist.

Problem A3
Eine Stadt plant den Bau eines Gemeinschaftsgartens, der 2/3 einer Quadratmeile abdeckt. Sie möchten es auf einer Weide eines alten Pferdehofes situieren. Eine Dimension des Gartenbereichs wird durch einen Zaun bestimmt, der 3/4 einer Meile lang ist. Verwenden Sie das Flächenmodell für die Division, um die andere Dimension des neuen Gartenbereichs zu bestimmen.

Aufgabe A4
Beschreiben Sie, wie das Flächenmodell zeigt, dass der Quotient zweier positiver Brüche, die jeweils kleiner als 1 sind, größer als der erste Bruch sein muss.

In diesem Teil: Das gemeinsame Nennermodell für die Division
Das Flächenmodell für die Division von Brüchen hilft nicht zu veranschaulichen, warum der Algorithmus, mit dem wir am besten vertraut sind (den Divisor invertieren und dann multiplizieren), funktioniert. Leider kann das kein Modell zeigen. Siehe Anmerkung 4 unten.

Aber hier ist ein anderer Teilungsalgorithmus, den wir mit einem Modell erklären können: Finden Sie den gemeinsamen Nenner, finden Sie die äquivalenten Brüche und teilen Sie die Zähler.

Um das Modell für diesen Algorithmus zu verstehen, gehen wir zuerst zurück, um einige der Konzepte der Division zu überprüfen. Es ist normalerweise einfacher zu berechnen, wenn Sie über die Division auf quotative Weise nachdenken. So können Sie sagen, dass 6 3 fragt: „Wie viele 3s gibt es in 6?“

Als nächstes müssen wir die Rolle der Einheiten in der Division verstehen.

Problem A5
Welche dieser Fragen liefert, wenn überhaupt, eine andere Antwort?
* Wie viele 3s gibt es in 6?
• Wie viele Gruppen von 3 Zehnern gibt es in 6 Zehnern?
* Wie viele Gruppen von 3 Fünfern gibt es in 6 Fünfern?
* Wie viele Gruppen von 3 Zehnteln gibt es in 6 Zehnteln?* Wie viele Gruppen von 3 @ s gibt es in 6 @s?
* Wie viele Gruppen von 3 Anythings gibt es in 6 Anythings (solange sich beide Anythings auf dieselbe Einheit beziehen)?

Der Punkt hier ist, dass die Einheiten des Problems keine Rolle spielen — wenn die Einheiten dieselbe Entität sind, verschwinden sie, wenn Sie teilen.

Dies bringt uns zurück zum neuen Algorithmus für die Division mit Brüchen: Um zwei Brüche zu teilen, finden Sie einen gemeinsamen Nenner und teilen Sie dann die Zähler.

Versuchen wir eine visuelle Version des Problems, das wir zuvor gemacht haben: 1/4 2/3. Finden Sie zuerst einen gemeinsamen Nenner:

1/4 2/3 = 3/12 8/12

Als nächstes teilen Sie die Zähler:

38 = 3/8

Hier ist das Modell für dieses Problem, das als gemeinsames Nennermodell bezeichnet wird:

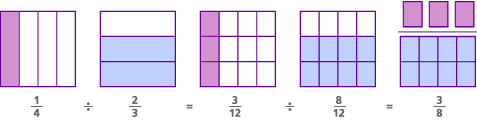
Bei diesem Problem lautete die ursprüngliche Frage: „Wie viele 2 / 3s gibt es in 1/4?“Indem wir einen gemeinsamen Nenner gefunden haben, haben wir die Frage in „Wie viele 8 / 12s gibt es in 3/12?“ – was ist das gleiche wie zu fragen „Wie viele 8s gibt es in 3?“ Die Antwort auf beide Fragen ist die gleiche: „Es gibt 3/8 einer 8 in 3.“

Problem A6
Verwenden Sie das Modell des gemeinsamen Nenners, um 3/5 durch 3/4 zu teilen.

Problem A7
Warum hat 0.6 0.2 die gleiche Antwort wie 6 2?

In diesem Teil: Übersetzen des Prozesses in Dezimalstellen
Sie können das, was Sie über Operationen und Brüche gelernt haben, auch auf Dezimalstellen erweitern. Denken Sie daran, dass eine abschließende Dezimalzahl als Bruch mit einer Potenz von 10 als Nenner betrachtet werden kann (z. B. 0,4 = 4/10). Siehe Anmerkung 5 unten.

Warum müssen wir die Dezimalstellen ausrichten, wenn wir Dezimalstellen addieren oder subtrahieren?
Wir müssen die Dezimalstellen ausrichten, da wir nur addieren oder subtrahieren können, wenn die Einheiten gleich sind. Indem wir die Dezimalstellen ausrichten, stellen wir sicher, dass wir Ziffern mit denselben Ortswerten addieren oder subtrahieren, genau wie beim Addieren oder Subtrahieren ganzer Zahlen.

Warum zählen wir die Dezimalstellen, wenn wir Dezimalstellen multiplizieren?
Aus dem Abschnitt über Exponenten in Sitzung 3 wissen wir, dass die Multiplikation mit Exponenten das Addieren oder „Zählen“ der Exponenten erfordert. So ist zum Beispiel 0,2 • 0,03 in der Exponentialform die folgende:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

Die Exponenten sind -1 und -2, die eine bzw. zwei Stellen rechts vom Dezimalpunkt liegen. Das Produkt hat dann einen Exponenten, der die Summe von -1 und -2 (dh -3) ist und drei Stellen rechts vom Dezimalpunkt liegt. Das Produkt von 0,2 • 0,03 ist 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

Warum verschieben wir die Dezimalstellen, wenn wir mit Dezimalstellen dividieren?
Dieser Prozess hängt mit der Suche nach äquivalenten Brüchen zusammen. Sie können sich die Division als Bruch vorstellen. Da das Problem 2.5 0.05 ist schwer zu visualisieren, schreiben Sie es als 2,5 / 0,05. Sie benötigen eine ganze Zahl im Nenner, also multiplizieren Sie mit 100, um eine ganze Zahl zu erhalten. Um die Multiplikation des Nenners mit 100 zu kompensieren, müssen Sie auch den Zähler mit 100 multiplizieren. Das bedeutet, dass Sie tatsächlich mit 100/100 oder 1 multipliziert haben, was den Wert des Bruchs nicht ändert. So sieht der Prozess aus: