Fracciones, Porcentajes y Proporciones Parte A: Modelos para la Multiplicación y División de Fracciones (45 minutos)

En esta Parte: Modelo de Área para Multiplicación
En el pasado, es posible que haya aprendido algoritmos particulares para la multiplicación y división de fracciones. Ahora vamos a usar algunos de los modelos visuales que hemos empleado anteriormente en este curso para comprender mejor lo que realmente sucede cuando realizamos estas operaciones. Véase la nota 2 infra.

Primero usaremos un modelo de área, uno que superpone cuadrados que se dividen en el número apropiado de regiones y se sombrean según sea necesario, para aclarar lo que sucede cuando se multiplican fracciones. Por ejemplo, así es como usaríamos el modelo de área para demostrar el problema 3/8 • 2/3:

Sombrear un cuadrado, dividido verticalmente, para representar 3/8 (se muestra a continuación en rosa):		Sombrear otro cuadrado, dividido horizontalmente, para representar 2/3 (se muestra a continuación en azul):		Superponga los dos cuadrados. El producto es el área con doble sombra (que se muestra a continuación en morado):

¿Cuál es el valor de esta área púrpura? Hay 3 * 2, o 6, partes moradas de 8 * 3, o 24, partes en total, por lo que el valor del área púrpura es 6/24.

Este modelo demuestra visualmente el algoritmo familiar: Multiplicar dos fracciones, multiplicar los numeradores y luego multiplicar los denominadores. Este algoritmo «cuenta» tanto las partes moradas (el producto de los dos numeradores) como el número total de partes (el producto de los dos denominadores).

También podemos usar este modelo para» reducir » la fracción. Primero intercambiamos las posiciones de algunas de las partes moradas. Dos de las partes moradas se pueden mover a la parte superior, y por lo tanto, dos de los octavos ahora están sombreados. Estos dos octavos son la misma área que un cuarto:

En esta Parte: Pruébelo Usted mismo
Haga sus propias transparencias cuadradas para superponerlas y modele la solución para cada paso del Problema A1 a continuación.

Problema A1
Una foto aérea de tierras de cultivo muestra las dimensiones de tres campos en fracciones de milla. Utilice el modelo de área que acaba de aprender a modelar el área en millas cuadradas de cada uno de estos campos:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

Problema A2
Describa cómo el modelo de área muestra que el producto de dos fracciones positivas, cada una menor que 1, debe ser más pequeño que cualquiera de las fracciones.

Segmento de vídeo
En este segmento, Jeanne y Liz utilizan el modelo de área para multiplicar fracciones. Relacionan este modelo con el algoritmo de multiplicación y comprueban formas de reducir visualmente las fracciones. Mira este segmento de video después de completar los problemas A1 y A2.

Puede encontrar este segmento en el video de la sesión aproximadamente 4 minutos y 32 segundos después del logotipo de Annenberg Media.

En esta Parte: Modelo de Área para División
Podemos aplicar el modelo de área para la multiplicación de fracciones para visualizar la división de dos fracciones cuando cada una es menor que 1. Para modelar la división con fracciones, invertimos más o menos el proceso utilizado para la multiplicación. Comenzamos con un área que estamos buscando, y encontramos uno de los factores que faltan que conforman esa área. Véase la nota 3 infra.

Por ejemplo, así es como usaríamos el modelo para demostrar el problema 1/4 2/3:

Sombrear un cuadrado, dividido verticalmente, para representar 1/4 (como en el modelo de multiplicación, está sombreado de color púrpura):		Superponga un cuadrado dividido en tercios, posicionado horizontalmente, en el cuadrado de las cuartas, y dibuje un soporte a la derecha del cuadrado de los tercios para mostrar el tamaño de 2/3:

Lo que vemos ahora es el morado (1/4) de la zona y el tamaño de uno de los factores que hicieron de esa área.

Sabemos por el modelo de multiplicación que el producto de 2/3 y otro factor (el cociente) define un área equivalente en tamaño a 1/4. Para encontrar el cociente, necesitamos mover la parte superior del área púrpura para que tenga la misma altura que el factor 2/3.

Subdividir el cuadrado de las cuartas para hacer un cuadrado de las octavas:		Mueva las dos piezas moradas superiores al área de 2/3 de altura (el área dentro del soporte de 2/3):		Ahora sombrea los rectángulos inmediatamente a la derecha e inmediatamente por encima del área púrpura:

Esto muestra que hay 3 * 2, o 6, partes moradas de 8 * 3, o 24, partes en total. El área púrpura es igual a 1/4, y vino del producto de 2/3 multiplicado por qué? Podemos ver que el otro factor es 3/8.

Problema A3
Un pueblo planea construir un jardín comunitario que cubrirá 2/3 de milla cuadrada. Les gustaría situarlo en un pasto de una antigua granja de caballos. Una dimensión del área del jardín estará determinada por una valla que mide 3/4 de milla de largo. Utilice el modelo de área para la división para determinar la otra dimensión de la nueva área de jardín.

Problema A4
Describa cómo el modelo de área muestra que el cociente de dos fracciones positivas, cada una menor que 1, debe ser mayor que la primera fracción.

En Esta Parte: El Modelo de Denominador Común para la División
El modelo de área para la división de fracciones no ayuda a ilustrar por qué funciona el algoritmo con el que estamos más familiarizados (invertir el divisor y luego multiplicar). Desafortunadamente, ningún modelo puede mostrar eso. Véase la nota 4 infra.

Pero aquí hay un algoritmo de división diferente, uno que podemos explicar con un modelo: Encontrar el denominador común, encontrar las fracciones equivalentes y dividir los numeradores.

Para comprender el modelo de este algoritmo, volvamos primero a repasar algunos de los conceptos de división. Por lo general, es más fácil de calcular si se piensa en la división de una manera citativa. Por lo tanto, se puede decir que 6 3 pregunta, » ¿Cuántos 3 hay en 6?»

A continuación, necesitamos comprender el papel de las unidades en la división.

Problema A5
¿Cuál de estas preguntas, en su caso, da una respuesta diferente?
* ¿Cuántos 3s hay en 6?
* ¿Cuántos grupos de 3 decenas hay en 6 decenas?
* ¿Cuántos grupos de 3 cincos hay en 6 cincos?
* ¿Cuántos grupos de 3 décimas hay en 6 décimas?•¿Cuántos grupos de 3 @s hay en 6 @s?
* ¿Cuántos grupos de 3 anythings hay en 6 anythings (siempre que ambos se refieran a la misma unidad)?

El punto aquí es que las unidades del problema no importan — si las unidades son la misma entidad, desaparecen cuando se divide.

Esto nos lleva de vuelta al nuevo algoritmo para la división con fracciones: Dividir dos fracciones, encontrar un denominador común y luego dividir los numeradores.

Probemos una versión visual del problema que hicimos antes: 1/4 2/3. En primer lugar, encontrar un denominador común:

1/4 2/3 = 3/12 8/12

a continuación, divida los numeradores:

38 = 3/8

Aquí es el modelo para este problema, llamado el común denominador del modelo:

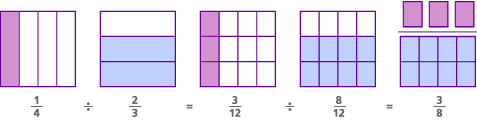
En este problema, en efecto, la pregunta original era «¿cuántos 2/3s hay en 1/4?»Al encontrar un denominador común, cambiamos la pregunta a» ¿Cuántos 8/12 hay en 3/12?»- que es lo mismo que preguntar » ¿Cuántos 8 hay en 3?»La respuesta a ambas preguntas es la misma:» Hay 3/8 de un 8 en 3.»

Problema A6
Utilice el modelo de denominador común para dividir 3/5 por 3/4.

Problema A7
¿Por qué 0.6 0.2 tiene la misma respuesta que 6 2?

En esta Parte: Traducir el Proceso a Decimales
Puede extender lo que ha aprendido sobre operaciones y fracciones a decimales también. Recuerde que un decimal de terminación se puede considerar como una fracción con una potencia de 10 como denominador (por ejemplo, 0.4 = 4/10). Véase la nota 5 infra.

¿Por qué necesitamos alinear los puntos decimales cuando sumamos o restamos decimales?
Necesitamos alinear los puntos decimales porque solo podemos sumar o restar si las unidades son las mismas. Al alinear los puntos decimales, nos aseguramos de sumar o restar dígitos que tengan los mismos valores de posición, al igual que cuando sumamos o restamos números enteros.

¿Por qué contamos los decimales cuando multiplicamos decimales?
De la sección sobre exponentes de la Sesión 3, sabemos que la multiplicación con exponentes requiere sumar, o» contar», los exponentes. Así, por ejemplo, 0.2 • 0,03 en la forma exponencial es la siguiente:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

Los exponentes son -1 y -2, que son uno y dos lugares, respectivamente, a la derecha del punto decimal. El producto tendrá entonces un exponente que es la suma de -1 y -2 (es decir, -3), y es de tres lugares a la derecha del punto decimal. El producto de 0,2 • 0.03 es 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

¿por Qué nos movemos los puntos decimales para dividir con decimales?
Este proceso está relacionado con la búsqueda de fracciones equivalentes. Puedes pensar en la división como una fracción. Desde el problema 2.5 0.05 es difícil de visualizar, escríbalo como 2.5 / 0.05. Necesitas un número entero en el denominador, así que multiplícalo por 100 para obtener un número entero. Para compensar la multiplicación del denominador por 100, también debe multiplicar el numerador por 100. Eso significa que realmente multiplicaste por 100/100, o 1, lo que no cambia el valor de la fracción. Este es el aspecto del proceso: